串联谐振电路
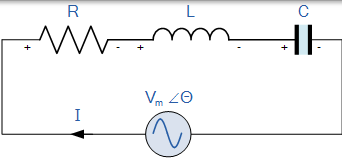
当电源频率使 L 和 C 两端的电压相等且相位相反时,谐振发生在串联电路中
到目前为止,我们已经分析了一串联 RLC 电路的行为,其电源电压是固定频率稳态正弦电源。我们在教程中也看到过串联 RLC 电路,可以使用相量组合两个或多个正弦信号,只要它们具有相同的频率电源。
但是,如果将固定幅度但不同频率的电源电压施加到电路上,那么电路的特性会发生什么。此外,由于这种变化的频率,电路“频率响应”行为会对两个无功分量产生什么影响。
在串联 RLC 电路中,电感器的感抗与电容器的容抗相等的频率点成为频率点。换言之,XL = XC。在发生这种情况的点被称为谐振频率点,( ƒR 电路),并且,因为我们正在分析串联 RLC 电路这个谐振频率产生串联谐振。
串联谐振电路是用于电气和电子电路的最重要的电路之一。它们可以以各种形式存在,例如 AC 电源滤波器,噪声滤波器以及无线电和电视调谐电路,产生用于接收不同频率信道的非常选择性的调谐电路。考虑下面的简单串联 RLC 电路。
串联 RLC 电路

首先,让我们定义一下我们对串联 RLC 电路的了解。
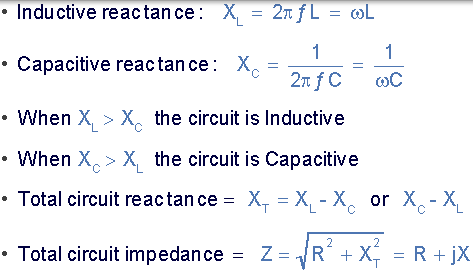
根据感应电抗的上述等式,如果频率或电感增加,则电感器的总感应电抗值也将增加。随着频率接近无穷大,电感器电抗也将朝着无穷大增加,其中电路元件起到开路的作用。
然而,当频率接近零或 DC 时,电感器电抗将减小到零,导致相反的效果像短路一样。这意味着感应电抗与频率 “成比例 ”,在低频时较小,在较高频率时较高,这在以下曲线中表明:
对频率的归纳电抗
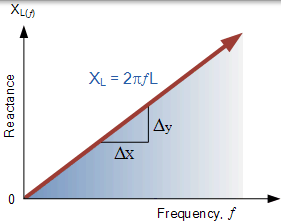
感应电抗对频率的曲线图是直线线性曲线。电感的感抗电抗值随着其上的频率增加而线性增加。因此,电感性电抗为正,是成正比的频率( XL αƒ)
对于上面的容抗电阻公式也是如此,但反之亦然。如果频率或电容增加,则总电容电抗将减小。当频率接近无穷大时,电容器电抗将减小到几乎为零,导致电路元件像 0Ω 的理想导体一样工作。
但是当频率接近零或直流电平时,电容器电抗会迅速增加到无穷大,导致它像一个非常大的电阻,变得更像开路状态。这意味着对于任何给定的电容值,容性电抗与频率 反比,如下所示:
对频率的电容反应
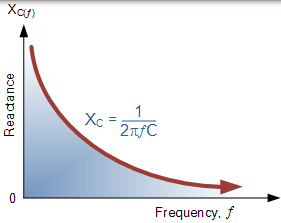
容抗与频率的关系图是双曲线。电容器的电抗值在低频时具有非常高的值,但随着其上的频率增加而迅速降低。因此,电容性电抗是负的并且是与频率成反比( Xc ^ αƒ-1)
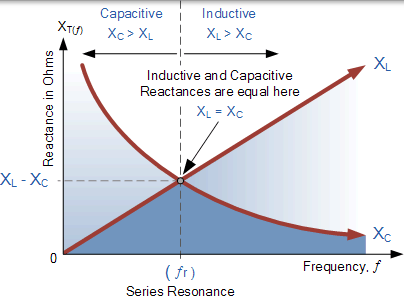
我们可以看到这些电阻的值取决于电源的频率。在较高频率下,XL 高,而低频率 XC 高。那么必须有一个频率点,XL 的值与 XC 的值相同,并且存在。如果我们现在将感应电抗曲线放在电容电抗曲线的顶部,使两条曲线在同一轴上,交点将给出串联谐振频率点,( ƒ[R 或 ωR),如下所示。
串联谐振频率
其中: ƒR 的单位是赫兹,大号是在亨利和 C 单位是法拉。
当相反且相等的两个电抗相互抵消时,在 AC 电路中发生电谐振,如 XL = XC, 并且图中发生这种情况的点是两个电抗曲线彼此交叉。在串联谐振电路中,谐振频率 fr 点可以如下计算。

然后我们可以看到,在谐振时,两个电抗相互抵消,从而使串联 LC 组合充当短路,而串联谐振电路中的电流仅与电阻 R 相反。在复杂形式中,谐振频率是串联 RLC 电路的总阻抗变为纯粹 “真实” 的频率,即不存在虚拟阻抗。这是因为在共振时它们被抵消了。因此,串联电路的总阻抗为电阻的只是值,并且因此: Z = R。
然后在谐振时,串联电路的阻抗处于其最小值并且仅等于电路的电阻 R. 谐振时的电路阻抗称为电路的“动态阻抗”,并且根据频率,XC (通常在高频)或 XL (通常在低频)将主导谐振的任一侧,如下所示。
串联谐振电路中的阻抗
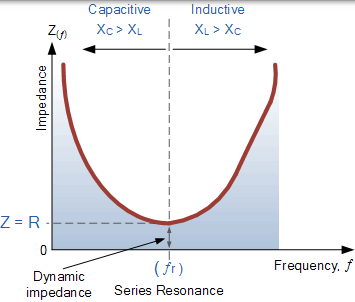
注意,当容抗在电路中占主导地位时,阻抗曲线本身具有双曲线形状,但是当感应电抗支配电路时,由于 XL 的线性响应,曲线是非对称的。
你还可能注意到,如果电路阻抗在谐振时最小,那么,电路导纳必须达到最大值,并且串联谐振电路的一个特性是导纳非常高。但这可能是一件坏事,因为谐振电阻值非常低意味着流过电路的电流可能危险地高。
我们从前一个关于串联 RLC 电路的教程中回忆起串联组合电压是 VR,VL 和 VC 的相量和。然后,如果在谐振时两个电抗相等并且取消,则表示 VL 和 VC 的两个电压也必须相反且值相等,从而相互抵消,因为对于纯组件,相量电压在+90o 处被吸收 和-90o 分别。
然后在串联谐振电路中,当 VL = -VC 时,所得的无功电压为零,并且所有电源电压在电阻器上下降。因此,VR = V电源,并且由于这个原因,串联谐振电路被称为电压谐振电路(与作为电流谐振电路的并联谐振电路相反)。
共振时串联 RLC 电路
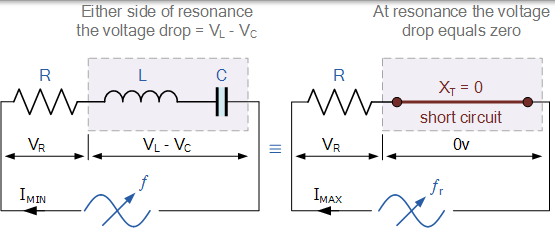
由于流过串联谐振电路的电流是电压除以阻抗的乘积,因此在阻抗谐振时,Z 处于其最小值( = R)。因此,该频率下的电路电流将处于其最大值 V / R,如下所示。
串联电路电流谐振
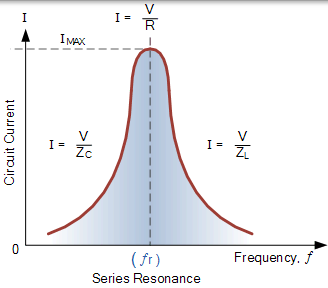
串联谐振电路的频率响应曲线显示电流的大小是频率的函数,并将其绘制在图表上,向我们显示响应从接近零开始,在 IMAX = I 时达到谐振频率的 最大值 当 ƒ 变为无限时, R 再次下降到接近零。其结果是电感器 L 和电容器 C 两端的电压大小即使在共振时也可以变得比电源电压大许多倍,但是当它们相等并且相反时它们相互抵消。
由于串联谐振电路仅在谐振频率上起作用,这种类型的电路也称为接收器**电路,**因为在谐振时,电路的阻抗最小,因此容易接受频率等于其谐振频率的电流。
你可能还注意到,由于谐振时通过电路的最大电流仅受电阻值(纯值和实际值)的限制,因此源电压和电路电流必须在此频率下彼此同相。然后,串联谐振电路的电压和电流之间的相位角也是固定电源电压的频率的函数,并且当谐振频率点为零时,V:I,VR 彼此同相为如下所示。因此,如果相位角为零,则功率因数必须为 1。
串联谐振电路的相角
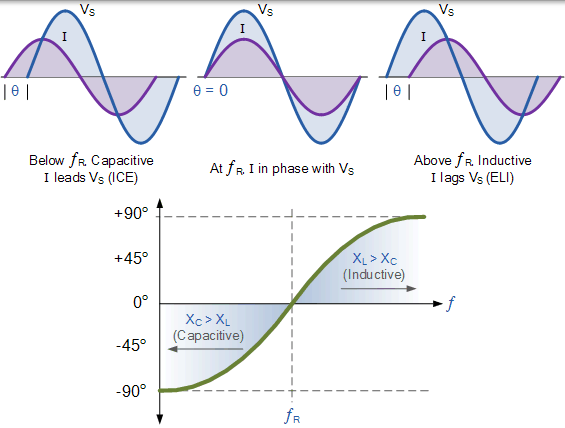
通知还,其中,相位角为阳性以上的频率 ƒř 和阴性以下的频率 ƒř 并且这可以通过被证明,
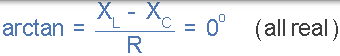
串联谐振电路的带宽
如果串联 RLC 电路由恒定电压的可变频率驱动,那么电流的大小 I 与阻抗 Z 成正比,因此在谐振时,电路吸收的功率必须处于其最大值,因为 P = I2 Z
如果我们现在减小或增加频率,直到串联谐振电路中电阻器吸收的平均功率是谐振时其最大值的一半,我们产生两个称为半功率点的频率点,从最大值开始下降-3dB,以 0dB 作为最大电流参考。
这些-3dB 点给我们一个电流值,该值是它的最大谐振值的 70.7%,其定义为: 0.5(I2 R)=(0.707×1)2 - [R。然后对应于较低频率以一半的功率的点被称为“较低的截止频率”,标记 ƒL 与对应于最高频率的点,同时半功率被称为“上限截止频率”,标记为 ƒ^ h。这两个点之间的距离,即( ƒH - ƒL)被称为带宽 (BW),并且是如图所示提供至少一半最大功率和电流的频率范围。
串联谐振电路的带宽
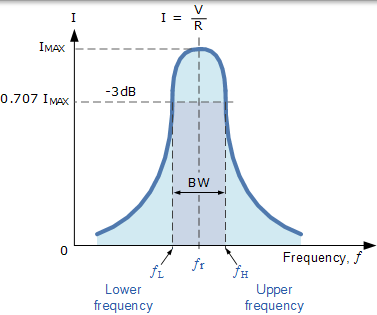
电路电流幅度的频率响应高于串联谐振电路中谐振的“锐度”。定量测量峰值的锐度,称为电路的品质因数 Q. 质量因子将存储在电路中的最大或峰值能量(电抗)与每个振荡周期期间消耗的能量(电阻)联系起来,这意味着它是谐振频率与带宽的比率,电路 Q 越高,越小带宽,Q =ƒR / BW。
当带宽在两个-3dB 点之间取得时,电路的选择性衡量其拒绝这些点两侧任何频率的能力。更具选择性的电路将具有更窄的带宽,而选择性更低的电路将具有更宽的带宽。的串联谐振电路的选择性可以通过仅调整电阻的值,保持所有其它部件是相同的,因为可以控制 Q =(XL 或 XC)/ R。
串联 RLC 谐振电路的带宽
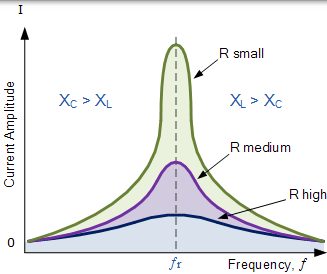
然后将串联谐振电路的谐振,带宽,选择性和品质因数之间的关系定义为:
1)。的谐振频率,(ƒR)
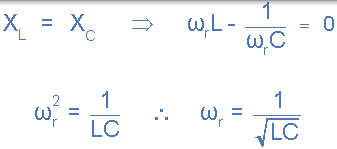
2)。目前,(I)
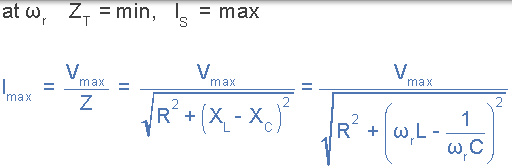
3)。较低的截止频率,(ƒL)
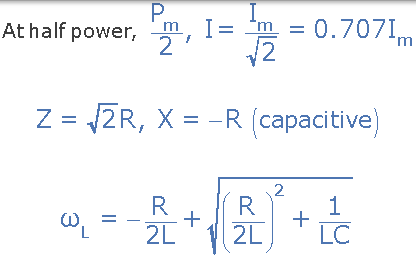
4)。上截止频率,(ƒH)
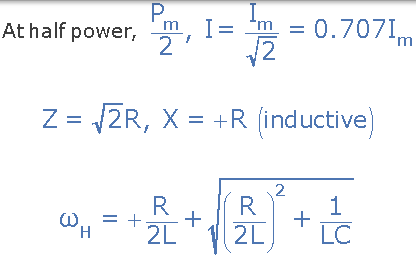
5)。带宽,(BW)

6)。品质因数,(Q)
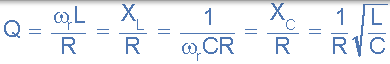
系列共振实例 No1
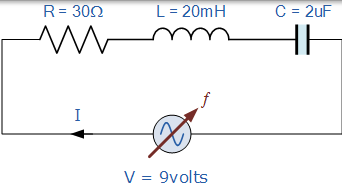
由 30Ω 电阻,2uF 电容和 20mH 电感组成的串联谐振网络连接在正弦电源电压上,该电压在所有频率下具有 9 伏的恒定输出。计算谐振频率,谐振电流,谐振时电感和电容两端的电压,电路的品质因数和带宽。还绘制所有频率的相应电流波形。
- 谐振频率, ƒř
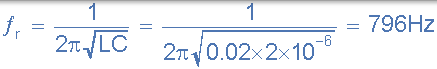
- 共振时的电路电流,Im
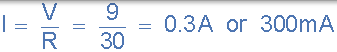
- 共振时的感应电抗,XL.

- 电感和电容两端的电压 VL,VC.

注意:电源电压可能只有 9 伏,但在谐振时,电容,VC 和电感上的无功电压 VL 为 30 伏峰值!
- 品质因素,Q
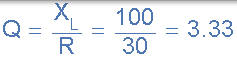
- 带宽,BW
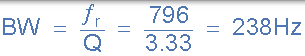
- 上下-3dB 频率点, ƒH 和 ƒL
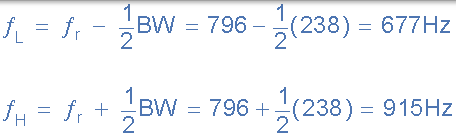
- 电流波形
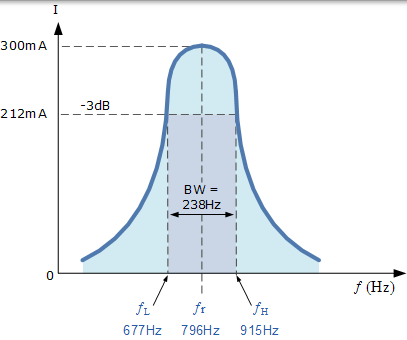
系列共振实例 No2
串联电路由 4Ω 的电阻,500mH 的电感和连接在 100V,50Hz 电源上的可变电容组成。计算产生串联谐振条件所需的电容,以及在谐振点处电感和电容两端产生的电压。
谐振频率 ƒ[R
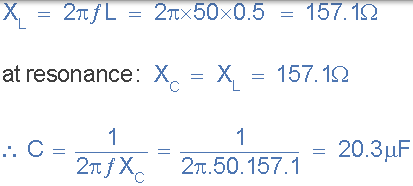
电感和电容两端的电压 VL,VC.

系列共振摘要
你可能已经注意到,在本教程的串联谐振电路分析中,我们研究了带宽,上下频率,-3dB 点和质量或 Q 因子。所有这些都是用于设计和构建带通滤波器(BPF)的术语,实际上,谐振电路用于 3 元件电源滤波器设计,以通过“通带”范围内的所有频率,同时拒绝所有其他频率。
但是,本教程的主要目的是分析和理解串联谐振在无源 RLC 串联电路中如何发生的概念。它们在 RLC 过滤器网络和设计中的使用超出了本特定教程的范围,所以不会在这里看到,抱歉。
- 为了在任何电路中发生谐振,它必须具有至少一个电感器和一个电容器。
- 谐振是电路振荡的结果,因为存储的能量从电感器传递到电容器。
- 当 XL = XC 并且传递函数的虚部为零时发生共振。
- 在谐振时,电路的阻抗等于 Z = R 时的电阻值。
- 在低频时,串联电路的电容为: XC > XL,这为电路提供了领先的功率因数。
- 在高频时,串联电路的电感为: XL > XC,这使电路具有滞后功率因数。
- 谐振时的高电流值会在电感和电容两端产生非常高的电压值。
- 串联谐振电路可用于构建高频选择滤波器。但是,其高电流和非常高的元件电压值会对电路造成损坏。
- 谐振电路的频率响应的最突出特征是其幅度特性中的尖锐谐振峰值。
- 由于阻抗最小且电流最大,串联谐振电路也称为接收器电路。
在下一篇关于并联谐振的教程中,我们将研究频率如何影响并联 RLC 电路的特性,以及此时并联谐振电路的 Q 因数如何决定其当前放大倍数。