并联 RLC 电路分析
该并联 RLC 电路是完全相反的,以我们在前面的教程看了看,虽然以前的一些概念和公式仍然适用的串联电路。
然而,并联 RLC 电路的分析在数学上可能比串联 RLC 电路更困难,因此在本教程中关于并联 RLC 电路,本教程中仅假设纯组件以保持简单。
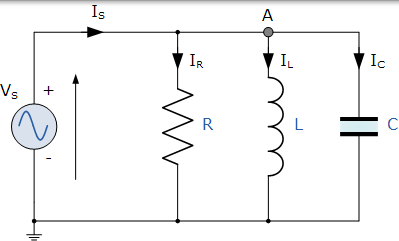
这次代替电路元件共用的电流,所施加的电压现在对所有人都是共同的,因此我们需要找到通过每个元件的各个分支电流。使用类似于 DC 并联电路的电路的电流来计算并联 RLC 电路的总阻抗 Z,此时的差异是使用导纳而不是阻抗。考虑下面的并联 RLC 电路。
并联 RLC 电路

在上述并联 RLC 电路中,我们可以看到电源电压 VS 对所有三个元件都是通用的,而电源电流 IS 则由三部分组成。流过电阻器的电流,IR,电流流过电感器,IL 和通过电容器的电流,IC。
但是流过每个分支并因此流过每个元件的电流将彼此不同并且与供电电流 IS 不同。从电源汲取的总电流不是三个独立分支电流的数学和,而是它们的矢量和。
与 RLC 系列电路一样,我们可以使用相量或矢量方法求解该电路,但这次矢量图将以电压作为参考,其中三个电流矢量相对于电压绘制。并联 RLC 电路的相量图是通过将每个元件的三个单独的相量组合在一起并矢量地添加电流而产生的。
由于电路两端的电压对于所有三个电路元件是共同的,因此我们可以将其用作参考矢量,其中三个电流矢量以相应的角度相对于此绘制。得到的矢量 IS 是通过将两个矢量 IL 和 IC 加在一起然后将该和加到剩余的矢量 IR 而得到的。在 V 和 IS 之间获得的角度 将是电路相位角,如下所示。
并联 RLC 电路的相量图
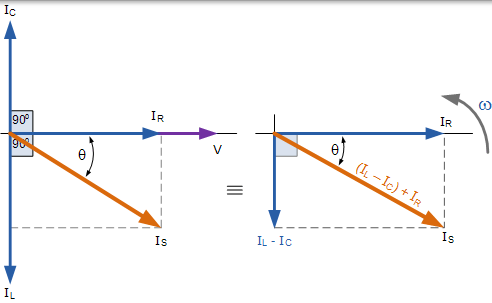
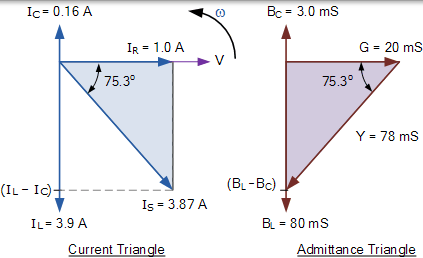
我们可以从右上方的相量图中看到,当前矢量产生一个矩形三角形,包括斜边 IS,水平轴 IR 和垂直轴 IL - IC 希望你会注意到,这形成了一个因此,当前三角形和我们可以在此当前三角形上使用毕达哥拉斯定理以数学方式获得沿 x 轴和 y 轴的分支电流的大小,然后确定总电流 IS 这些组件如图所示。
并联 RLC 电路的当前三角形
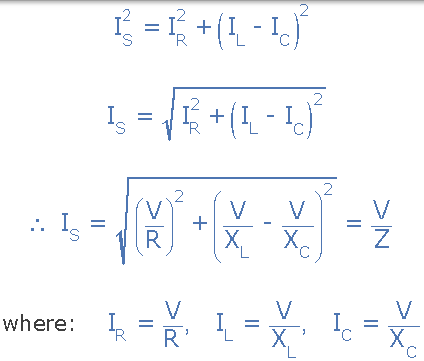
由于电路两端的电压对所有三个电路元件都是通用的,因此可以使用基尔霍夫电流定律(KCL)找到通过每个分支的电流。基尔霍夫的现行定律或结法则规定“进入结点或节点的总电流与离开该节点的电流完全相等”,因此进出节点 A 的电流如下:
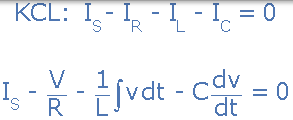
取导数,用 C 除以上式并重新排列,得到以下电路电流的二阶方程。它成为二阶方程,因为电路中有两个电抗元件,即电感和电容。
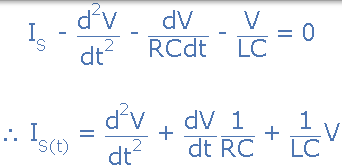
在这种类型的 AC 电路的反对电流流动是由三个部分组成: XL XC 和 - [R 与这三个值赋予电路阻抗的组合 Z。我们从上面知道,并联 RLC 电路的所有组件中的电压具有相同的幅度和相位。然后,还可以根据流过的电流和每个元件上的电压数学地描述每个部件上的阻抗。
并联 RLC 电路的阻抗
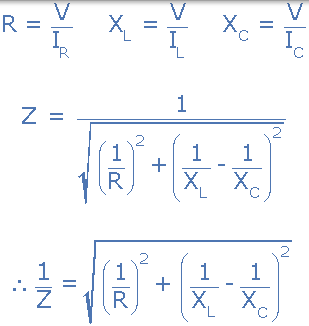
你会注意到,并联 RLC 电路的最终公式为每个并联支路产生复阻抗,因为每个元件变为阻抗的倒数,( 1 / Z),阻抗的倒数称为导纳。
在并联 AC 电路中,使用导纳,符号( Y)来解决复杂的分支阻抗更为方便,特别是当涉及两个或更多并联分支阻抗时(有助于数学)。通过添加并联导纳可以简单地找到电路的总导纳。那么电路的总阻抗 ZT 将为 1 / YT Siemens,如图所示。
并联 RLC 电路的导纳
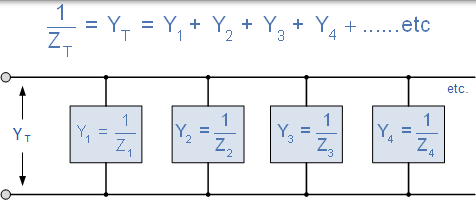
准入新的单位是*西门子,缩写为小号,(旧单元姆欧的 ℧ ,欧姆的反向)。导纳在并联分支中加在一起,而阻抗在串联分支中加在一起。但是,如果我们可以得到阻抗的倒数,我们也可以得到电阻和电抗的倒数,因为阻抗由两个分量 R 和 X 组成。然后,电阻的倒数称为电导,电抗的倒数称为电纳。
电导,准入和接受
用于电导,导纳和电纳的单位都是相同的,即西门子(S),它也可以被认为是欧姆或欧姆-1 的倒数,但每个元素使用的符号是不同的,并且在纯组件中给出如下:
准入(Y):
电导(G):
| 电导性,的倒数 - [R 和被赋予该符号 ģ 。电导定义为当施加 AC 或 DC 电压时电阻器(或一组电阻器)允许电流流动的容易程度。 | 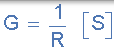 |
资助(B):
因此,我们可以将感应和电容电纳定义为:

在 AC 串联电路中,对电流的反对是阻抗,Z 具有两个分量,电阻 R 和电抗,X,并且从这两个分量中我们可以构造阻抗三角形。类似地,在并联 RLC 电路中,导纳 Y 也有两个分量,电导,G 和电纳,B。这使得可以构造具有水平电导轴 G 和垂直电纳轴的导纳三角形,jB 如图所示。
并联 RLC 电路的导纳三角形
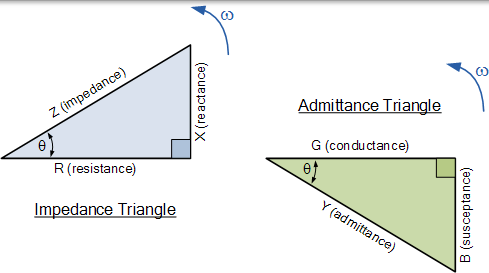
现在我们有一个导纳三角形,我们可以使用毕达哥拉斯来计算所有三个边的大小以及相位角,如图所示。
来自毕达哥拉斯
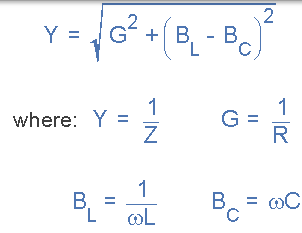
然后我们可以定义电路的导纳和导纳的阻抗,如下:
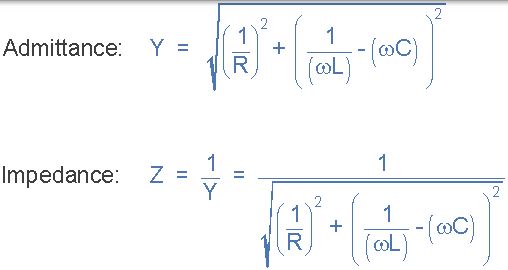
给我们一个功率因数角度:
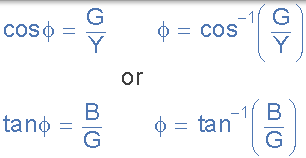
作为导纳,并联 RLC 电路的 Y 是复数量,对应于串联电路的阻抗 Z = R + jX 的一般形式的导纳将被写为 Y = G-jB,用于并联电路,其中实部 G 是电导和虚部 jB 是电纳。在极地形式中,这将给出:
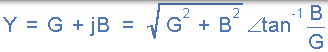
并联 RLC 电路示例 No1
一个 1kΩ 电阻,一个 142mH 线圈和一个 160uF 电容都通过 240V,60Hz 电源并联。计算并联 RLC 电路的阻抗和从电源汲取的电流。
并联 RLC 电路的阻抗
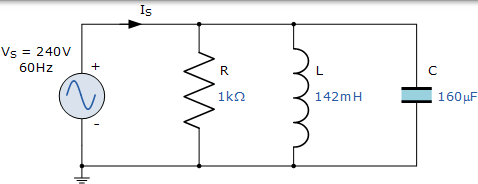
在交流电路中,电阻不受频率影响,因此 R =1kΩ
感应电抗,( XL):

电容电抗,( XC):

阻抗,( Z):
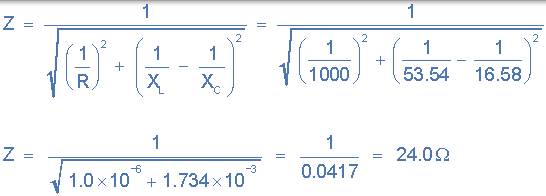
供电电流,( Is):
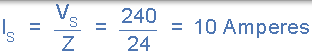
并联 RLC 电路示例 No2
一个 50Ω 电阻,一个 20mH 线圈和一个 5uF 电容都通过 50V,100Hz 电源并联。计算从电源汲取的总电流,每个支路的电流,电路的总阻抗和相角。还构造表示电路的电流和导纳三角形。
并联 RLC 电路
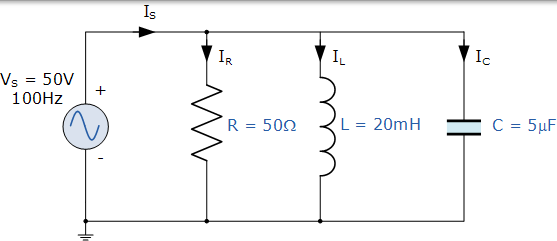
1)。感应电抗,( XL):
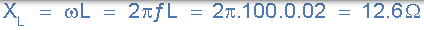
2)。电容电抗,( XC):
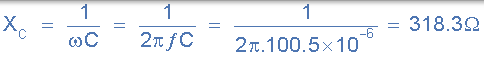
3)。阻抗,( Z):
4)。电流通过电阻 R( IR):
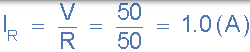
5)。通过电感的电流 L( IL):
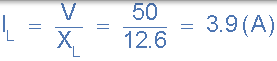
6)。电流通过电容 C( IC):

7)。总供电电流,( IS):

8)。电导,( G):
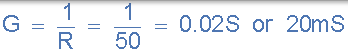
9)。感应电纳,( BL):
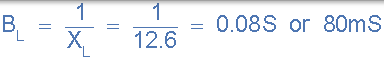
10)。电容保护,( BC):
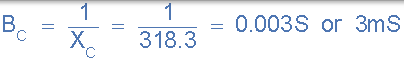
11)。准入,( Y):
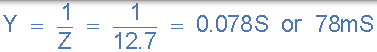
12)。合成电流和电源电压之间的相角( φ):
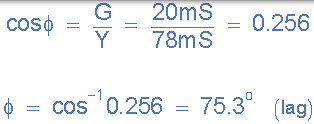
电流和导纳三角形
并联 RLC 电路概述
在包含电阻器,电感器和电容器的并联 RLC 电路中,电路电流 IS 是由三个分量 IR,IL 和 IC 组成的相量和,其中所有三个分量都是电源电压。由于电源电压对所有三个元件都是通用的,因此在构造电流三角形时它用作水平参考。
可以使用与串联 RLC 电路相同的矢量图来分析并联 RLC 网络。然而,当并联 RLC 电路包含两个或更多个电流分支时,对于并联 RLC 电路的分析在数学上比对于串联 RLC 电路更难。因此,可以使用称为导纳的阻抗的倒数来容易地分析 AC 并联电路。
导纳是符号 Y 的阻抗的倒数。与阻抗一样,它是由实部和虚部组成的复数量。实部是电阻的倒数,称为电导,符号 Y,而虚部是电抗的倒数,称为电纳,符号 B,复数形式表示为: Y = G + jB,两者之间具有二元性阻抗定义为:
| 系列电路 | 并联电路 |
| 电压,(V) | 目前,(I) |
| 阻力,(R) | 电导率,(G) |
| 电抗,(X) | 继承,(B) |
| 阻抗,(Z) | 准入,(Y) |
由于电纳是电抗的倒数,在电感电路中,感应电纳,BL 的值为负值,而在容性电路中,电容电纳,BC 的值为正值。与 XL 和 XC 完全相反。
到目前为止,我们已经看到串联和并联 RLC 电路在同一电路中包含容抗和电抗。如果我们改变整个这些电路的频率,其中所述电容性电抗的值等于存在必须成为一个点感抗,因此,那 XC ^ = XL。
发生这种情况的频率点称为谐振,在下一个教程中,我们将研究串联谐振以及它的存在如何改变电路的特性。