相量图和相量代数

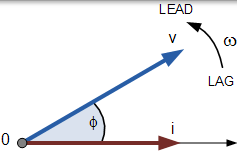
相量图是一种表示两个或多个交变量之间的大小和方向关系的图形方式

相同频率的正弦波形可以在它们之间具有相位差，其表示两个正弦波形的角度差。此外，术语超前和滞后以及同相和异相通常用于表示一个波形与另一个波形的关系，其中广义正弦表达式如下： A(t) = Am sin(ωt±Φ) 表示时域形式的正弦曲线。

但是，当以这种方式以数学方式呈现时，有时难以使两个或更多个正弦波形之间的角度或相量差异可视化。克服该问题的一种方法是通过使用相量图以空间或相量域形式在图形上表示正弦曲线，并且这通过旋转矢量方法实现。

基本上，旋转矢量，简称为相量，是缩放线，其长度表示具有在某个时间点“冻结”的幅度（“峰值幅度”）和方向（“相位”）的 AC 量。

相量是在一端具有箭头的矢量，其部分地表示矢量（ V 或 I） 的最大值，并且部分地表示旋转的矢量的末端。

通常，假设矢量在一端围绕称为“原点”的固定零点旋转，而表示数量的箭头端在一个角速度下以逆时针方向自由旋转。矢量的这种逆时针旋转被认为是正旋转。同样，顺时针旋转被认为是负旋转。

尽管术语矢量和相量都用于描述本身具有幅度和方向的旋转线，但两者之间的主要区别在于矢量幅度是正弦波的峰值，而相量幅度是 RMS 值的正弦曲线。在两种情况下，相位角和方向保持不变。

任何时刻的交变量的相位可以用相量图表示，因此相量图可以被认为是“时间函数”。可以通过以 ω=2π 的角速度旋转的单个矢量来构造完整的正弦波，其中 f 是波形的频率。然后，相量是具有“幅度”和“方向”的量。

通常，当构造相量图时，总是假设正弦波的角速度 ω 以 rad/sec 为单位。考虑下面的相量图。

正弦波形的相量图

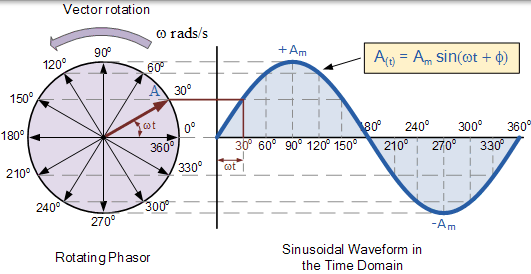
当单个矢量沿逆时针方向旋转时，其在 A 点的尖端将进行一个 360o 或 2π 的完整旋转，代表一个完整的循环。如果其移动尖端的长度在时间上以不同的角度间隔传递到如上所示的曲线图，则将在零时间从左侧开始绘制正弦波形。沿水平轴的每个位置表示从零时间开始经过的时间，t = 0。当矢量是水平时，矢量的尖端表示 0°、180° 和 360o。

同样地，当向量的前端垂直它所代表的正峰值 Am 在 90o 或 π/ 2 时，以及负峰值 -Am 在 270o 或 3π/ 2。然后波形的时间轴表示相量移动的角度或弧度。因此，我们可以说相量代表旋转矢量的缩放电压或电流值，该旋转矢量在某个时间点（ t） 被“冻结”，在上面的例子中，是 30° 的角度。

有时，当我们分析交流波形时，我们可能需要知道相量的位置，表示某个特定时刻的交变量，特别是当我们想要比较同一轴上的两个不同波形时，例如，电压和电流。我们在上面的波形中假设波形在时间 t = 0 开始，相应的相角为度或弧度。

但是，如果第二个波形开始于此零点的左侧或右侧，或者我们希望以相量符号表示两个波形之间的关系，那么我们将需要考虑波形的这个相位差 Φ。请考虑上一个相位差教程中的下图。

正弦波形的相位差

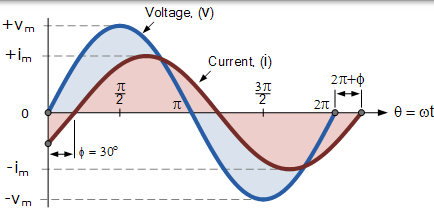
定义这两个正弦量的广义数学表达式将写为：

$$ \begin{array} { l } { \mathrm { V } _ { ( \mathrm { t } ) } = V _ { \mathrm { m } } \sin ( \omega \mathrm { t } ) } \\ { \mathrm { i } _ { ( \mathrm { t } ) } = \mathrm { I } _ { \mathrm { m } } \sin ( \omega \mathrm { t } - \phi ) } \end{array} $$

电流 i 滞后于电压 v 的角度为 Φ，在上面的例子中，是 30o。因此，表示两个正弦量的两个相量之间的差异是角度 Φ，并且得到的相量图将是，

正弦波形的相量图

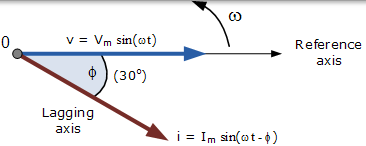
对应于水平轴上的时间零（ t = 0） 绘制相量图。相量的长度与绘制相量图的瞬间电压（V）和电流（I）的值成比例。当两个相量如前所述沿逆时针方向旋转时，电流相量滞后电压相量角度 Φ，因此角度 Φ 也在相同的逆时针方向上测量。

但是，如果波形在时间 t = 30o 时冻结，相应的相量图将如右图所示。由于两个波形具有相同的频率，因此电流相量再次落后于电压相量。

然而，由于电流波形现在在此时刻穿过水平零轴线，我们可以使用电流相量作为我们的新参考，并正确地说电压相量将电流相量“超前”角度 Φ。无论哪种方式，一个相量被指定为参考相量，并且所有其他相量将相对于该参考超前或滞后。

相量相加

有时在研究正弦曲线时需要将两个交流波形加在一起，例如在 AC 串联电路中，它们彼此不同相。如果它们是同相的，则没有相移，那么它们可以以与 DC 值相同的方式加在一起，以找到两个矢量的代数和。例如，如果分别为 50 伏和 25 伏的两个电压同相，则它们将以相加的形成 75 伏（50 + 25）的一个电压。

然而，如果它们不同相，即它们不具有相同的方向或起始点时，需要将它们之间的相位角考虑进来，用向量图通过平行四边形法则来决定它们的相量和或矢量和。

考虑两个交流电压，V1 具有 20 伏的峰值电压，V2 为 30 伏的峰值电压，其中 V1 超前 V2 60o。两个电压的总电压 VT 可以通过首先画出表示两个矢量的矢量图，然后构造一个平行四边形，其中两个边是电压，V1 和 V2。如下所示。

两个相量的相量加法

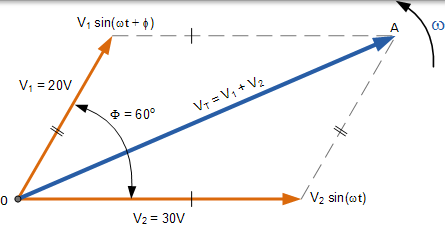
通过绘制两个相量以缩放到方格纸上，通过测量从零点到交叉点的对角线的长度（称为合成矢量），可以很容易地找到 V1 + V2 它们的相量和 - 线 0-A。这种图形方法的缺点是在绘制相量尺时需要耗费时间。

此外，虽然此图形方法提供的答案对于大多数目而言足够准确，但如果未精确绘制或未按比例绘制，则可能会产生错误。然后，通过分析方法确保始终获得正确答案的一种方法。

在数学上将两个电压加在一起，我们可以通过首先找到它们的垂直和水平方向，然后由此我们可以计算得到的合成向量 VT 的“垂直”和“水平”分量。这种使用余弦和正弦规则来找到该结果值的分析方法通常称为矩形形式。

在矩形形式中，相量被分成实部 x 和虚部 y，形成广义表达式 Z = x±jy。 （我们将在下一个教程中更详细地讨论这个问题）。然后，这给出了一个表示正弦电压幅度和相位的数学表达式：

复杂正弦波的定义

$$ V _ { m } = \cos ( \phi ) + j V _ { m } ( \sin \phi ) $$

因此，使用先前的广义表达式将两个向量 A 和 B 相加，如下所示，

$$ \begin{array} { l l } { A = x + j y } & { B = w + j z } \\ { A + B = ( x + w ) + j ( y + z ) } \end{array} $$

使用矩形形式的相量加法

电压 V2 沿着水平轴的参考方向，幅值为 30 V，然后它具有水平分量但没有垂直分量。

• 水平分量 = 30 cos 0o = 30 伏
• 垂直分量 = 30 sin 0o = 0 伏

然后，这给出了电压 V2 的矩形表达式 ： 30 + j0

电压，20 伏的 V1 超前 V2 60o，然后它具有如下的水平和垂直分量。

• 水平分量 = 20 cos 60o = 20 x 0.5 = 10 伏

• 垂直分量 = 20 sin 60o = 20 x 0.866 = 17.32 伏

• • 然后，这给出了电压 V1 的矩形表达式 ： 10 + j17.32

通过如下将水平和垂直分量加在一起得到合成电压 VT，

• VHorizontal = V1 和 V2 的实部之和 = 30 + 10 = 40 伏
• VVertical = V1 和 V2 的虚部之和 = 0 + 17.32 = 17.32 伏

现在，无论是实数和虚数值已经计算出电压的幅度，VT 是通过简单地使用毕达哥拉斯定理来计算，

$$ \mathrm { V } _ { \mathrm { T } } = \sqrt { 实部 ^ { 2 } + 虚部 ^ { 2 } } \\ \mathrm { V } _ { \mathrm { T } } = \sqrt { 40 ^ { 2 } + 17.32 ^ { 2 } } $$

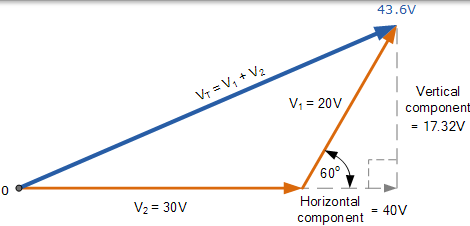
然后得到的相量图将是：

VT 的 结果值

相量减法

相量减法与上述矩形加法非常相似，除了此时矢量差是 V1 和 V2 的两个电压之间的平行四边形的另一个对角线，如图所示。

两个相量的矢量减法

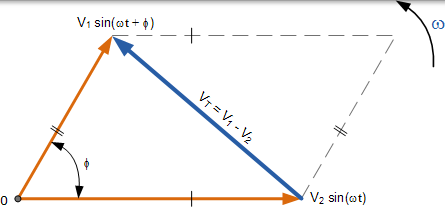
这次不是将水平和垂直分量加在一起，而是将相减。

$$ \begin{array} { l l } { A = x + j y } & { B = w + j z } \\ { A - B = ( x - w ) + j ( y - z ) } \end{array} $$

三相相量图

以前我们只研究了单相交流波形，其中单个多匝线圈在磁场内旋转。但如果三个具有相同匝数的线被放置在相同的转子轴上，彼此相隔 120o 电角度，将产生的三相电压电源。

平衡的三相电压源由三个单独的正弦电压组成，这些电压在幅度和频率上都相等，但彼此相位差正好为 120o 电角度。

标准做法是将三个阶段的颜色编码为红色，黄色和蓝色，以识别每个单独的相，红色相作为参考相。三相供应的正常旋转顺序是红色，接着是黄色，接着是蓝色，（ R，Y，B）。

与上面的单相相量一样，表示三相系统的相量也围绕中心点沿逆时针方向旋转，如标记为 ω 的箭头所示，以 rad/s 为单位。三相平衡星形或三角形连接系统的相量如下所示。

三相相量图

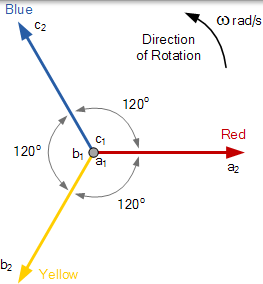
相电压的大小都相等，但相位角只有不同。线圈的三个绕组在点 a1，b1 和 c1 处连接在一起，以产生用于三个单独相的共同中性连接。然后，如果将红相作为参考相，则可以相对于公共中性点定义每个单独的相电压。

三相电压方程

$$ \begin{aligned} \text { RedPhase: } & \mathrm { V } _ { \mathrm { RN } } = \mathrm { V } _ { \mathrm { m } } \sin \theta \\ \text { Yellow Phase: } & \mathrm { V } _ { \mathrm { YN } } = \mathrm { V } _ { \mathrm { m } } \sin \left( \theta - 120 ^ { \circ } \right) \\ \text { Blue Phase: } \mathrm { V } _ { \mathrm { BN } } & = \mathrm { V } _ { \mathrm { m } } \sin \left( \theta - 240 ^ { \circ } \right) \\ or, \mathrm { V } _ { \mathrm { BN } } & = \mathrm { V } _ { \mathrm { m } } \sin \left( \theta + 120 ^ { \circ } \right) \end{aligned} $$

如果将红相电压 VRN 作为前面所述的参考电压，则相序将为 R - Y - B，因此黄相中的电压滞后 VRN 120o，蓝相中的电压滞后 VYN 也是 120o。但我们也可以说蓝相电压 VBN 将红相电压 VRN 超前 120o。

关于三相系统的最后一点。由于三个单独的正弦电压彼此之间具有固定的关系 120o 相移，因此它们被称为平衡，因为在一组平衡的三相电压中，它们的相量和总是为零： Va + Vb + Vc = 0

相量图摘要

然后总结一下关于相量图的重点知识。

最简单的来说，相量图是旋转矢量在水平轴上的投影，表示瞬时值。由于可以绘制相量图以表示任何时刻，因此任何角度，交变量的参考相量总是沿着正 x 轴方向绘制。

• 矢量，相量和相量图仅适用于正弦交流交流量。
• 相量图可用于在任何时刻表示两个或更多个固定的正弦量。
• 通常，参考相量沿水平轴绘制，并且在该时刻绘制其他相量。所有相量均参考水平零轴绘制。
• 可以绘制相量图来表示两个以上的正弦曲线。它们可以是电压，电流或其他一些交变量，但它们的频率必须相同。
• 所有相量都沿逆时针方向旋转。据说参考相量之前的所有相量都是超前，而参考相量后面的所有相量都被称为滞后。
• 通常，相量的长度表示正弦量的 rms 值而不是其最大值。
• 由于矢量的速度不同，不同频率的正弦波不能在相同的相量图上表示。在任何时刻，它们之间的相位角将是不同的。
• 可以将两个或更多个向量一起添加或减去，并成为单个向量，称为结果向量。
• 向量的水平边等于实数或 x 向量。向量的垂直边等于虚数或 y 向量。合成的直角三角形的斜边等同于合成向量。
• 在三相平衡系统中，每个相位移相 120°。

在下一个关于 AC 理论的教程中，我们将把正弦波形表示为矩形形式的复数，极性形式和指数形式。