RC 波形

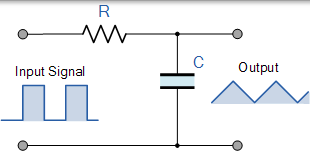
当周期性波形应用于其输入时，RC 电路可以产生有用的输出波形，例如方波，三角波和锯齿波。

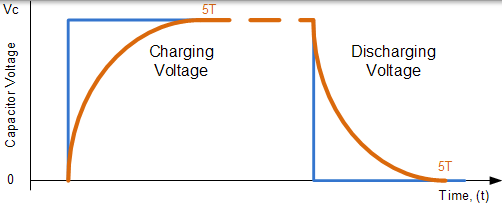
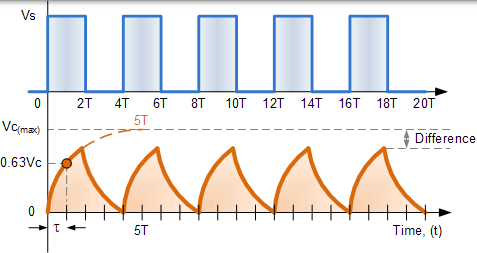
在之前的 RC 充电和放电教程中，我们了解了电容器如何通过串联电阻器自行充电和放电。当施加或去除恒定的 DC 电压时，该电容器完全充电或完全放电所花费的时间等于 5 个 RC 时间常数或 5T。

但是如果我们将这种恒定的直流电源改变为脉冲或方波波形会发生什么情况，该波形不断地以其时间周期或频率确定的速率从最大值变化到最小值。对于给定的 RC 时间常数值，这会如何影响 RC 波形输出 ？

我们之前看到，当施加电压时，电容器充电至 5T，而当电压被移除时，电容器放电至 5T。在 RC 充电和放电电路中，该 5T 时间常数值始终一致，因为它由电阻 - 电容（RC）组合固定。然后，只能通过改变电容器本身或电路中的电阻器的值来改变对电容器完全充电或放电所需的实际时间，如下所示。

典型的 RC 波形

方波信号

通过使用具有所需时间常数的 RC 电路可以获得有用的波形。如果我们将连续方波电压波形应用于 RC 电路，其脉冲宽度恰好与电路的 5RC 时间常数（ 5T） 相匹配，那么电容器两端的电压波形将如下所示：

5RC 输入波形

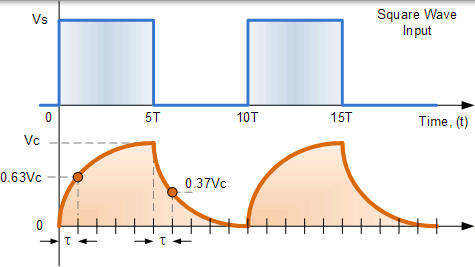
电容两端的电压降在充电至 Vc 和根据输入电压放电至零之间交替变化。在这个例子中，输入方波电压波形的频率（以及因此得到的时间周期，f = 1 / T）与 5RC 时间常数的频率恰好匹配两倍。

该 10RC 时间常数允许电容器在输入波形的 ON 周期（ 0 至 5RC） 期间完全充电，然后在 OFF 期间（ 5 至 10RC） 完全放电，从而实现完美匹配的 RC 波形。

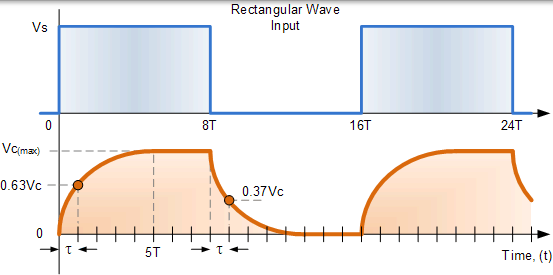
如果输入波形的时间周期变长（较低频率，ƒ<1 / 10RC），例如相当于 8RC 的 ON 半周期脉冲宽度，则电容器将保持更长的充电时间并保持不变完全放电更长，产生 RC 波形，如图所示。

更长的 8RC 输入波形

但是，如果我们现在减少输入波形的总时间周期（更高频率，ƒ> 1 / 10RC），比如说 4RC ，电容器将没有足够的时间在 ON 期间完全充电或在 OFF 期间完全放电。因此，电容器上的合成电压降 Vc 将小于其最大输入电压，从而产生如下所示的 RC 波形。

更短的 4RC 输入波形

然后，通过改变 RC 时间常数或输入波形的频率，我们可以改变电容器两端的电压，从而产生 Vc 和时间 t 之间的关系。这种关系可用于改变各种波形的形状，使电容器两端的输出波形几乎与输入波形相似。

频率响应

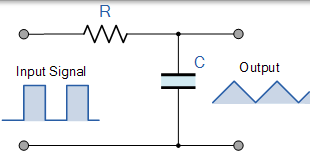
RC 积分器

积分器是一种类型的低通滤波器电路，一个方波输入信号转换成一个三角波形的输出。如上所述，如果 5RC 时间常数与输入 RC 波形的时间周期相比较长，则所得输出将为三角形，输入频率越高，输出幅度与输入相比就越低。

从中我们得出积分器的理想电压输出为：

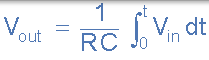
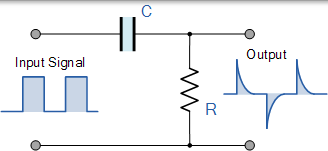
RC 微分器

微分器是一个高通滤波器类型电路的，可以在其输出的方波输入信号转换为高频尖峰。如果 5RC 时间常数与输入波形的时间周期相比较短，那么电容器将在输入周期的下一次更改之前更快地充满电。

当电容器充满电时，电阻两端的输出电压为零。输入波形的下降沿到达导致电容器反向充电，产生负输出尖峰，然后随着方波输入在每个周期期间变化，输出尖峰从正值变为负值。

从中可以得到差分器的理想电压输出：

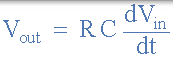
交替正弦波输入信号

如果我们现在将这些 RC 电路的输入 RC 波形更改为正弦波正弦波电压信号的输入 RC 波形，则结果输出 RC 波形将保持不变，并且仅影响其幅度。通过改变电阻器，R 或电容器 C 的位置，可以根据输入频率值对这两个电路的频率响应进行简单的一阶低通或高通滤波器。

低频信号从输入端传递到输出端，衰减很小或没有衰减，而高频信号则衰减到几乎为零。高通滤波器电路也是如此。通常，在输出幅值已经下降 3 分贝（截止频率点 ƒC）来用于定义滤波器带宽，这里 3 分贝的损失对应于输出电压的降为原始值的 70.7%。

RC 滤波器截止频率

其中 RC 是先前定义的电路的时间常数，可以用 τ 代替。这是时域和频域概念如何相关连的另一个示例。