RC 微分器

无源 RC 微分器是串联的 RC 网络，其产生对应于微分的数学过程的输出信号。

对于无源 RC 微分电路，输入连接到电容器，而输出电压来自与* RC 积分电路*完全相反的电阻。

无源 RC 微分器只不过是与电阻串联的电容，这是一种频率相关器件，它具有与固定电阻串联的电抗（与积分器相反）。与积分电路一样，输出电压取决于电路 RC 时间常数和输入频率。

因此，在低输入频率下，电容器的电抗 Xc 阻断任何直流电压或缓慢变化的输入信号。在高输入频率时，电容器电抗很低，允许快速变化的脉冲直接从输入端传递到输出端。

这是因为电容电抗（Xc）与电阻（R）的比率对于不同的频率是不同的，频率越低，输出越少。因此，对于给定的时间常数，随着输入脉冲的频率增加，输出脉冲越来越像输入脉冲的形状。

我们在关于无源高通滤波器的教程中看到了这种效应，如果输入信号是正弦波，则** RC 微分器**将简单地用作具有与 RC 对应的截止或转角频率的简单高通滤波器（HPF），其串联网络的时间常数（τ）。

因此，当用纯正弦波馈电时，由于 Xc = 1 /（2πC）的标准电容电抗公式，RC 微分电路用作简单的无源高通滤波器。

但是，也可以配置简单的 RC 网络以执行输入信号的区分。我们从之前的教程中知道，通过电容器的电流是一个复数指数，由下式给出：iC = C（dVc / dt）。电容器充电（或放电）的速率与电阻量和电容量成正比，给出电路的时间常数。因此，RC 微分电路的时间常数是等于 R 和 C 的乘积的时间间隔。考虑下面的基本 RC 串联电路。

RC 微分电路

对于 RC 微分器电路中，输入信号被施加到与该电阻两端所采取的输出的电容器的一侧，则 V OUT 等于 V - [R。由于电容器是频率相关元件，所以在板上建立的电荷量等于电流的时域积分。也就是说，电容器完全充电需要一定的时间，因为电容器不能瞬间充电，只能指数充电。

我们在关于* RC 积分器*的教程中看到，当单级电压脉冲施加到 RC 积分器的输入时，如果 RC 时间常数足够长，则输出变为锯齿波形。RC 微分器也将改变输入波形，但与积分器的方式不同。

电阻器电压

我们之前说过，对于 RC 微分器，输出等于电阻两端的电压，即：V OUT 等于 V R 并且是电阻，输出电压可以瞬间改变。

然而，电容器两端的电压不能立即改变，而是取决于电容 C 的值，因为它试图在其板上存储电荷 Q. 然后电流流入电容器，即我吨取决于在其板上的电荷的变化的速率。因此，电容器电流与电压不成比例，而是与其时间变化成比例，给出：i = dQ / dt。

当电容器板上的电荷量等于 Q = C x Vc，即电容乘以电压时，我们可以推导出电容器电流的等式：

电容器电流

因此，电容器电流可写为：

由于 VOUT等于 VR，其中根据欧姆定律的 VR也等于：iR x R。流过电容器的电流也必须流过电阻，因为它们都串联连接在一起。从而：

因此，RC 微分电路的标准公式为：

RC 微分公式

然后，我们可以看出，输出电压 VOUT 是输入电压 VIN的导数，由 RC 的常数进行加权。其中 RC 表示串联电路的时间常数 τ。

单脉冲 RC 微分器

当单个步进电压脉冲首先施加到 RC 微分器的输入时，电容器“最初出现”为快速变化信号的短路。这是因为方波的正向边缘的斜率 dv/dt 非常大（理想地是无限的），因此在信号出现的瞬间，所有输入电压都通过电阻器上出现的输出。

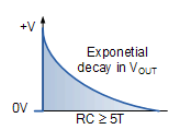
在输入信号的初始正向边沿经过并且输入的峰值恒定后，电容器开始以正常方式通过电阻器响应输入脉冲以 RC 时间确定的速率充电常数，τ= RC。

随着电容器充电，电阻器两端的电压以及输出电压以指数方式降低，直到电容器在 5RC（5T）的时间常数后变为完全充电，导致电阻器两端的输出为零。因此，完全充电电容器两端的电压等于输入脉冲的值，如下：VC = VIN，只要输入脉冲的幅度不变，该条件就成立。

如果现在输入脉冲改变并返回到零，则脉冲的负向边缘的变化率通过电容器到达输出，因为电容器不能响应这种高 dv/dt 变化，结果是输出端出现负增长。

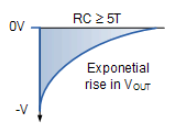
在输入信号的初始负向边沿之后，电容器恢复并开始正常放电，电阻器两端的输出电压以及输出电压随着电容器放电而开始呈指数增加。

因此，无论何时输入信号快速变化，输出端都会产生电压尖峰，该电压尖峰的极性取决于输入是正向还是负向变化，因为正向产生正尖峰。输入信号的边沿，以及由于负输入信号而产生的负尖峰。

因此，RC 微分器输出实际上是输入信号的变化率的曲线图，其与方波输入波没有相似之处，但是当输入脉冲改变值时由窄的正和负尖峰组成。

通过改变方波输入脉冲的时间周期 T 相对于串联组合的固定 RC 时间常数，输出脉冲的形状将如图所示改变。

RC 微分器输出波形

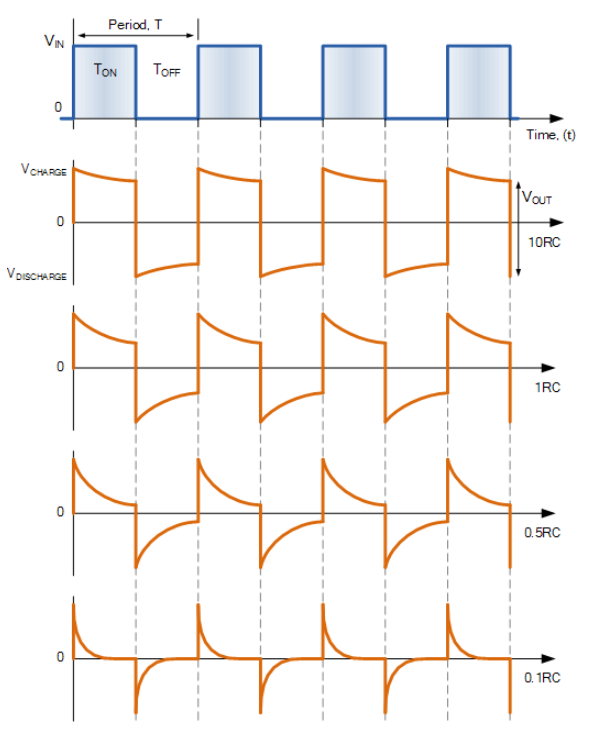
然后我们可以看到输出波形的形状取决于脉冲宽度与 RC 时间常数之比。当 RC 比脉冲宽度大得多（大于 10RC）时，输出波形类似于输入信号的方波。当 RC 比脉冲宽度小得多（小于 0.1RC）时，输出波形采用非常尖锐和窄的尖峰形式，如上所示。

因此，通过将电路的时间常数从 10RC 变为 0.1RC，我们可以产生一系列不同的波形。通常在 RC 微分电路中总是使用较小的时间常数，以在 R 上的输出端提供良好的尖锐脉冲。因此，方波脉冲的差分（高 dv/dt 阶跃输入）是无限短的尖峰，导致 RC 微分电路。

假设方波波形的周期 T 为 20ms，脉冲宽度为 10ms（20ms 除以 2）。为使尖峰放电至其初始值的 37％，脉冲宽度必须等于 RC 时间常数，即 RC = 10ms。如果我们选择电容值 C，1uF，那么 R 等于 10kΩ。

为了使输出类似于输入，我们需要 RC 为脉冲宽度值的十倍（10RC），因此对于电容值，例如 1uF，这将给出一个 100kΩ 的电阻值。同样，为了使输出类似于尖锐脉冲，我们需要 RC 为脉冲宽度的十分之一（0.1RC），因此对于相同的电容值 1uF，这将给出一个电阻值：1kΩ，依此类推。

RC 微分器示例

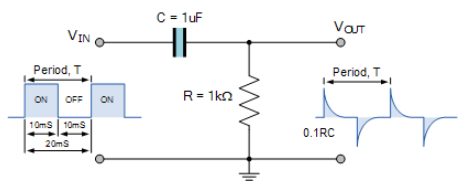
因此，通过将 RC 值设置为脉冲宽度的十分之一（并且在我们的示例中，这是 0.1 x 10ms = 1ms）或更低，我们可以在输出端产生所需的尖峰，并且给定脉冲宽度的 RC 时间常数越低，尖峰更尖锐。因此，输出波形的确切形状取决于 RC 时间常数的值。

RC 微分器摘要

我们在此** RC 差分器**教程中已经看到，输入信号被施加到电容器的一侧，输出通过电阻器获得。微分电路用于产生用于定时电路应用的触发或尖峰类型脉冲。

当方波步进输入应用于该 RC 电路时，它在输出端产生完全不同的波形。输出波形的形状取决于输入方波的周期时间 T（也可以说是频率 f）和电路的 RC 时间常数值。

当输入波形的周期时间也类似于或者比电路 RC 时间常数（更高频率）更短时，输出波形类似于输入波形，即方波轮廓。当输入波形的周期时间远长于（较低频率）电路 RC 时间常数时，输出波形类似于窄的正和负尖峰。

输出的正尖峰由输入方波的前沿产生，而输出的负尖峰由输入方波的下降沿产生。然后 RC 微分电路的输出取决于输入电压的变化率，因为效果非常类似于微分数学函数。