RC 积分器
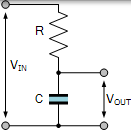
RC 积分器是串联的 RC 网络,其产生对应于积分的数学过程的输出信号。
对于无源 RC 积分器电路,输入连接到电阻,而输出电压取自电容器,与 RC 微分电路完全相反。输入为高电平时电容器充电,输入电压低时放电。
在电子学中,基本串联电阻 - 电容(RC)电路具有从基本充电/放电电路到高阶滤波器电路的许多用途和应用。这个双组件无源 RC 电路可能看起来很简单,但是根据所施加的输入信号的类型和频率,该基本 RC 电路的行为和响应可能非常不同。
无源 RC 网络只不过是与电容器串联的电阻器,即与电容器串联的固定电阻,其具有频率相关的电抗,其随着其板上的频率增加而减小。因此,在低频时,电容的电抗 Xc 很高,而在高频时,由于 Xc = 1 /(2πC)的标准电容电抗公式,其电抗很低,我们在关于无源低通滤波器的教程中看到了这种效应。
然后,如果输入信号是正弦波,RC 积分器将简单地充当低通滤波器(Low Pass Filter),其截止或转角频率对应于串联网络的 RC 时间常数(τ)和其输出降低到此截止频率点以上。因此,当用纯正弦波馈电时,RC 积分器充当无源低通滤波器。
正如我们之前所见,RC 时间常数反映了电阻和电容之间的关系,时间以秒为单位,与电阻 R 和电容 C 成正比。
因此,充电或放电的速率取决于 RC 时间常数,τ= RC。考虑下面的电路。
RC 积分器
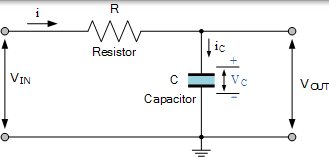
对于 RC 积分电路,输入信号被施加到与电容器两端取输出的阻力,则 VOUT 等于 VC。由于电容器是频率相关元件,所以在板上建立的电荷量等于电流的时域积分。也就是说,电容器完全充电需要一定的时间,因为电容器不能瞬间充电,只能指数充电。
因此,电容器电流可写为:
上述 iC = C(dVc / dt)的基本方程也可以表示为电荷的瞬时变化率,Q 相对于时间给出以下标准方程: iC = dQ / dt 其中电荷 Q = C x Vc,即电容乘以电压。
电容器充电(或放电)的速率与电阻和电容的量成正比,给出电路的时间常数。因此,RC 积分电路的时间常数是等于 R 和 C 的乘积的时间。
由于电容等于 Q / Vc,其中电荷 Q 是电流(i)在一定时间 (t) 内的流动,即 i x t 的乘积,从欧姆定律我们知道电压(V)相等对于 i x R,将这些代入 RC 时间常数的等式给出:
RC 时间常数
然后我们可以看到,当 i 和 R 都抵消时,只有 T 表示 RC 积分器电路的时间常数具有以秒为单位的时间维度,用希腊字母 τ 来表示。请注意,此时间常数反映了电容器充电至最大电压的 63.2%或放电至最大电压的 36.8%所需的时间(以秒为单位)。
电容器电压
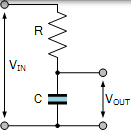
我们此前曾表示,为 RC 积分,输出等于电容两端的电压,即为:VOUT 等于 VC。该电压与电荷成比例,Q 存储在由下式给出的电容器上:Q = VxC。
结果是输出电压是输入电压的积分,积分量取决于 R 和 C 的值,因此取决于网络的时间常数。
我们在上面看到,电容器电流可以表示为电荷变化率 Q 相对于时间。因此,根据微积分的基本规则,Q 相对于时间的导数是 dQ / dt,并且当 i = dQ / dt 时,我们得到以下关系:
Q =∫idt (任何时刻电容器上的电荷 Q)
由于输入连接到电阻器,相同的电流,我必须通过电阻器和电容器(iR = iC) ,在电阻器两端产生 VR 电压降,因此电流,(i)流过该 RC 网络如下所示:
因此:
因为 i = VIN / R 时,替换和重新排列以求解 VOUT 作为时间的函数给出:
换句话说,RC 积分电路的输出,即电容两端的电压等于输入电压的时间积分 VIN 加权 1 / RC 的常数。其中 RC 代表时间常数 τ。
然后假设电容器上的初始电荷为零,即 VOUT = 0,输入电压 VIN 恒定,输出电压 VOUT 在时域中表示为:
RC 积分器公式
因此,RC 积分器电路是输出电压 VOUT 与输入电压的积分成正比的电路,考虑到这一点,让我们看看当我们以阶跃电压的形式施加单个正脉冲时会发生什么。RC 积分电路。
单脉冲 RC 积分器
当单级电压脉冲施加到 RC 积分器的输入端时,电容器响应脉冲通过电阻器充电。然而,输出不是瞬时的,因为电容器两端的电压不能瞬间改变,而是随着电容器以由 RC 时间常数 τ= RC 确定的速率充电而呈指数增加。
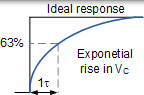
我们现在知道电容器充电或放电的速率取决于电路的 RC 时间常数。如果施加理想的阶跃电压脉冲,即前沿和后沿被认为是瞬时的,则电容器两端的电压将随充电而增加,并随着时间的推移而逐渐减小,其速率由下式确定:
电容器充电
电容器放电
| 时间 τ | 电容器充电 | 电容器放电 |
|---|---|---|
| 0.5 | 39.4% | 60.6% |
| 0.7 | 50% | 50% |
| 1 | 63.2% | 36.7% |
| 2 | 86.4% | 13.5% |
| 3 | 95.0% | 4.9% |
| 4 | 98.1% | 1.8% |
| 5 | 99.3% | 0.67% |
注意,在 5 个时间常数或更长时间后,电容器被认为是 100%完全充电或完全放电。
现在让我们假设我们有一个 RC 积分器电路,由一个 100kΩ 电阻和一个 1uF 电容组成,如图所示。
RC 积分电路示例
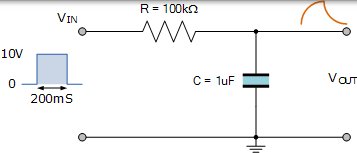
因此,RC 积分电路的时间常数 τ 为:RC =100kΩ×1uF = 100ms。
因此,如果我们将一个阶跃电压脉冲施加到输入端,其持续时间为两个时间常数(200mS),那么从上表中可以看出电容器将充电至其完全充电值的 86.4%。如果该脉冲具有 10 伏的幅度,那么这相当于 8.64 伏,然后当输入脉冲返回到零时,电容器再次通过电阻器放电回到源。
如果我们假设电容器允许在 5 个时间常数的时间内完全放电,或者在下一个输入脉冲到达之前 500mS,那么充电和放电曲线图将如下所示:
RC 积分器充电/放电曲线
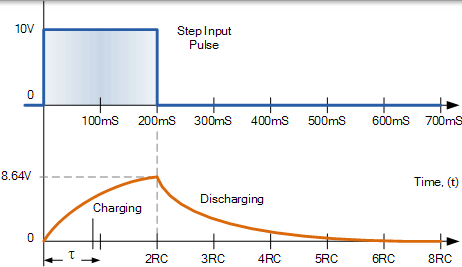
注意,电容器的初始值为 8.64 伏(2 个时间常数),而不是 10 伏输入。
然后我们可以看到,当 RC 时间常数固定时,输入脉冲宽度的任何变化都会影响 RC 积分电路的输出。如果脉冲宽度增加并且等于或大于 5RC,则输出脉冲的形状将类似于输入的形状,因为输出电压达到与输入相同的值。
然而,如果脉冲宽度减小到 5RC 以下,则电容器将仅部分充电而未达到最大输入电压,从而导致较小的输出电压,因为电容器不能充电,导致输出电压与输入的积分成比例电压。
因此,如果我们假设输入脉冲等于一个时间常数,即 1RC,则电容器将在 0 伏特和 10 伏特之间充电和放电,但在变化时电容器两端的电压的 63.2%和 38.7%之间。请注意,这些值由 RC 时间常数确定。
固定 RC 积分器时间常数
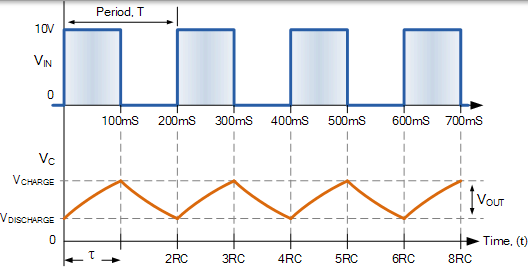
因此,对于连续脉冲输入,输入的周期时间与电路的 RC 时间常数之间的正确关系,输入的积分将产生一种斜升,然后产生斜降输出。但是为了使电路作为积分器正常工作,RC 时间常数的值必须大于输入周期时间。那是 RC»T,通常是 10 倍。
这意味着输出电压的大小(与 1 / RC 成比例)在高压和低压之间将非常小,严重衰减输出电压。这是因为电容器在脉冲之间充电和放电的时间要少得多,但平均输出直流电压将增加到输入的一半,在上面的脉冲示例中,这将是 5 伏(10/2)。
RC 积分器作为正弦波发生器
我们已经在上面看到,RC 积分器电路可以通过施加脉冲输入来执行积分操作,从而由于电容器的充电和放电特性而导致斜升和斜降三角波输出。但是如果我们改变过程并将三角波形应用于输入会发生什么,我们会得到脉冲或方波输出吗?
当 RC 积分电路的输入信号是脉冲形输入时,输出是三角波。但是当我们应用三角波时,由于斜坡信号随时间的积分,输出变为正弦波。
有许多方法可以产生正弦波形,但是电子产生正弦波型波形的一种简单而廉价的方法是使用一对串联连接在一起的无源 RC 积分电路,如图所示。
正弦波 RC 积分器
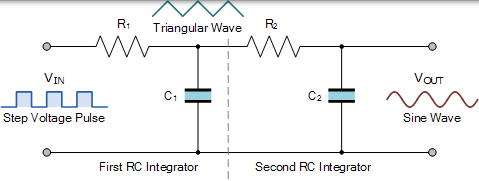
这里,第一个 RC 积分器将原始脉冲整形输入转换为斜升和斜降三角波形,该波形成为第二个 RC 积分器的输入。第二个 RC 积分器电路将三角波形的点对齐,将其转换为正弦波,因为它有效地对原始输入信号执行双积分,RC 时间常数影响积分程度。
由于斜坡的积分产生正弦函数(基本上是舍入的三角波形),其以赫兹为单位的周期频率将等于原始脉冲的周期 T. 另请注意,如果我们反转此信号并且输入信号是正弦波,则电路不会充当积分器,而是作为具有正弦波的简单低通滤波器(LPF),纯波形不会改变形状,只有它的幅度受到影响。
RC 积分器摘要
我们在这里看到 RC 积分器基本上是一个串联 RC 低通滤波器电路,当一个阶跃电压脉冲施加到其输入端时,产生的输出与其输入的积分成比例。这产生的标准方程: VO =∫Vi DT 其中 Vi 是供给到积分器的信号和 V 0 是积分输出信号。
输入阶跃函数的积分产生类似三角斜坡函数的输出,其幅度小于原始脉冲输入的幅度,衰减量由时间常数确定。因此,输出波形的形状取决于电路的时间常数与输入脉冲的频率(周期)之间的关系。
RC 积分器的时间常数总是与输入的周期 T 进行比较,因此长的 RC 时间常数将产生与输入信号相比具有低幅度的三角波形状,因为电容器具有较少的完全充电或放电时间。短时间常数允许电容器更多时间充电和放电,产生更典型的圆形形状。
通过将两个 RC 积分器电路并联连接,可以实现对输入脉冲的双重积分。这种双重积分的结果是第一积分电路将阶跃电压脉冲转换成三角波形,第二积分电路通过舍入三角波形的点来转换三角波形,产生正弦波输出波形,大大减少振幅。