电容和充电

电容器以电荷的形式将电能存储在其板上

电容器由两个平行的导电板（通常是金属）组成，它们被称为“电介质”的绝缘材料防止彼此接触（分离）。当向这些板施加电压时，电流以相对于电源电压的正电荷向一个板充电，而另一个板以相等且相反的负电荷充电。

然后，电容器具有能够存储电子的电荷 Q （以库仑为单位）的能力。当电容器完全充电时，其板之间存在电位差，pd 和板的面积越大和/或它们之间的距离越小（称为分离），电容器可以容纳的电荷就越大，它的电容就越大。

电容器在其板之间存储该电荷（ Q）的能力与所施加的电压 V 成比例，对于已知电容的电容器，以法拉为单位。请注意，电容 C 始终为正，从不为负。

施加的电压越大，存储在电容器极板上的电荷就越大。同样，施加的电压越小，电荷越小。因此，电容板上的实际电荷 Q 可以计算为：

对电容器充电

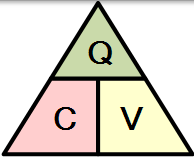
其中： Q （充电，以库仑计）= C （电容，单位为法拉）x V （电压，单位为伏特）

通过使用图片有时更容易记住这种关系。这里三个量的 Q，C 和 V 叠加成三角形，在顶部给电荷，底部有电容和电压。这种安排代表电容器充电公式中每个数量的实际位置。

并且转置上面的等式给出了以下相同等式的组合：

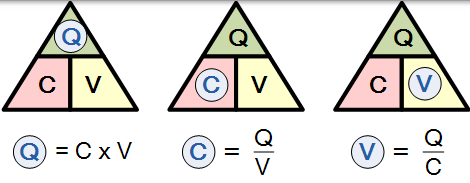
单位： Q 以库仑为单位测量，V 以伏特为单位，C 以法拉为单位。

然后从上面我们可以定义电容的单位为库仑/伏特，其也被称为法拉，单位 F 。

由于电容代表电容器在其板上存储电荷的能力（容量），我们可以将一个法拉定义为电容器的电容，其需要一个库仑的电荷以在其板之间建立一伏的电位差。。因此，电容越大，对于相同电压量，电容器上存储的电荷量就越高。

电容器在其导电板上存储电荷的能力使其具有电容值。电容也可以根据板的尺寸或面积，A 和板之间的介电材料的性质来确定。介电材料的量度由介电常数，（ ε）或介电常数给出。因此，表达电容器电容的另一种方法是：

电容器以空气为电介质

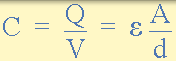
电容器以固体为电介质

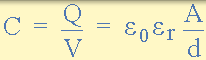
其中 A 是平板面积，m2 面积越大，电容器可以存储的电荷越多。d 是两个板之间的距离或间隔。这个距离越小，电极板存储电荷的能力就越高，因为-Q 带电电极板上的-ve 电荷对+ Q 带电电极板的影响更大，导致更多的电子被+排斥。Q 充电板，从而增加整体充电量。

ε 0 （ε）是介电常数为空气，其值是 8.84×10-12 F / m 和 ε R 是在两个板之间所使用的电介质的介电常数。

平行板电容器

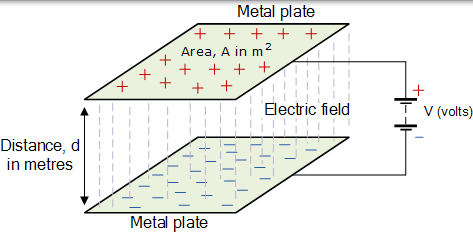
我们以前曾表示，平行板电容器的电容正比于表面积甲和反比于距离 d 的两个板之间，这对于空气的电介质如此。然而，通过在导电板之间插入介电常数大于空气的介电常数，可以增加电容器的电容值。

各种常用介电材料的典型 ε 值为 ： 空气= 1.0，纸= 2.5 - 3.5，玻璃= 3 - 10，云母= 5 - 7 等。

与空气相比，介电材料或绝缘体增加电容器电容的因素被称为介电常数 （k）。 k 是所用介电介质的介电常数与自由空间介电常数之比，也称为真空。

因此，所有电容值都与真空的介电常数有关。具有高介电常数的介电材料是比具有较低介电常数的介电材料更好的绝缘体。介电常数是无量纲的，因为它相对于自由空间。

电容示例 No1

平行板电容器由两个板组成，总表面积为 100cm2。如果板间距为 0.2 厘米，电容器的微微法拉电容（pF）是多少，所用的电介质是空气。

那么电容的值是 44pF。

电容器的充电和放电

考虑以下电路。

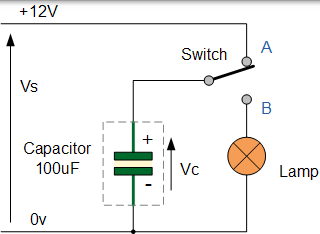
假定电容器完全放电并连接至所述电容器的开关刚被移动至位置甲。此时 100uF 电容器两端的电压为零，充电电流（i）开始向电容器充电，直到电路板上的电压等于 12v 电源电压。充电电流停止流动，电容器被称为“完全充电”。然后，Vc = Vs = 12v。

一旦电容器在理论上“完全充电”，即使供电电压已经断开，它也将保持其电压充电状态，因为它们充当一种临时存储装置。然而，虽然“理想”电容器可能也是如此，但由于内部泄漏电流流过电介质，实际电容器将在很长一段时间内缓慢放电。

这是一个需要记住的重点，因为即使电源电压“关闭”，连接在高压电源上的大值电容仍然可以保持大量电量。

如果此时开关断开，电容器将无限期地保持其电荷，但由于内部漏电流流过其电介质，电容器将非常缓慢地开始自身放电，因为电子通过电介质。电容器放电至其电源电压的 37％所需的时间称为时间常数 。

如果开关现在从位置 A 移动到位置 B，则完全充电的电容器将开始通过现在连接在其上的灯放电，照亮灯直到电容器完全放电，因为灯的元件具有电阻值。

灯的亮度和照明持续时间最终取决于电容器的电容值和灯的电阻（ t = R * C）。电容器的值越大，灯的发光越亮越长，因为它可以存储更多的电荷。

电容器充电示例 No2

计算上述电容器电路中的电荷。

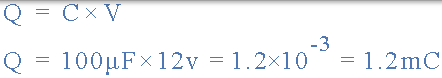
那么电容器上的电荷是 1.2 毫库仑。

电流通过电容器

由于两个极板之间的介电材料的绝缘特性，电流实际上不能流过电容器，因为它是电阻器或电感器。然而，两个板的充电和放电产生电流流动的效果。

流过电容器的电流与板上的电荷直接相关，因为电流是电荷相对于时间的流速。由于电容器在其极板之间存储电荷（ Q）的能力与施加的电压（ V） 成比例，因此电流和施加到电容器极板的电压之间的关系变为：

电流 - 电压（IV）关系

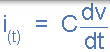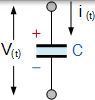随着板上的电压随时间增加（或减小），流过电容的电流从其板沉积（或移除）电荷，其中电荷量与施加的电压成比例。然后，施加到电容的电流和电压都是时间函数，并由符号 i(t) 和 v(t)表示。

但是，根据上式，我们还可以看到，如果电压保持不变，电荷将变为常数，因此电流将为零！ 换句话说，电压没有变化，没有电荷移动和没有电流。这就是当连接到稳态 DC 电压时电容器似乎“阻塞”电流的原因。

法拉

我们现在知道电容器存储电荷的能力给它的电容值 C，其单位为法拉，F 。但法拉本身就是一个非常大的单位，因此使用它是不切实际的，因此使用标准法拉单位的子多数或分数。

为了了解 Farad 究竟有多大，需要制作一个仅为 1 法拉的电容器所需的板的表面积，在真空中操作合理的板间距仅为 1mm。如果我们重新排列上面的电容等式，我们将得到一个板面积：

A = Cd÷8.85pF / m =（1×0.001）÷8.85×10-12 = 112,994,350 m2

或 1.13 亿米 2 这将是相当于 10 公里以上×10 千米（超过 6 英里）的正方形的板。那是巨大的。

具有一法拉或更大值的电容器倾向于具有固体电介质并且“一法拉”是如此大的单位使用，前缀用于电子公式中，其中电容器值以微法（ μF）给出，纳米-Farads（ nF）和 pico-Farads（ pF）。例如：

法拉的子单位

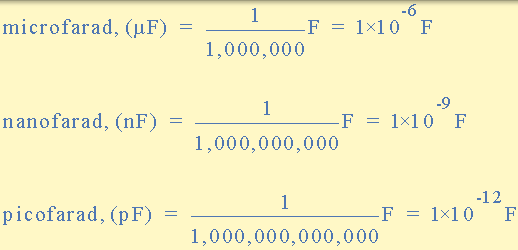
将以下电容值从 a） 22nF 转换为 μF，b） 0.2μF 转换为 nF，c） 550pF 转换为 μF。

a2 2nF =0.022μF

b0 .2μF= 200nF

c5 50pF =0.00055μF

虽然一个法拉是一个很大的价值，但电容现在通常可用，电容值为几百法拉，其名称反映了“超级电容器”或“超级电容器”的名称。

这些电容器是电化学能量存储装置，其利用其碳电介质的高表面积来传递比传统电容器高得多的能量密度，并且电容与碳的表面积成比例，碳越厚，电容越大。

低电压（约 3.5V 至 5.5V）超级电容器由于其高电容值而能够存储大量电荷，因为存储在电容器中的能量等于 1/2（C×V2）。

低压超级电容器通常用于便携式手持设备中，以取代大型，昂贵且重型锂电池，因为它们具有类似电池的存储和放电特性，使其非常适合用作替代电源或用于存储器备份。手持设备中使用的超级电容器通常使用安装在设备上的太阳能电池充电。

正在开发用于混合动力电动汽车和替代能源应用的超级电容器，以取代大型传统电池以及车辆音频和视频系统中的 DC 平滑应用。超级电容器可以快速充电，并具有非常高的储能密度，使其成为电动汽车应用的理想选择。

电容器中的能量

当电容器从连接到其的电源充电时，建立静电场，其将能量存储在电容器中。存储在该静电场中的焦耳能量等于电压供应用于维持电容器极板上的电荷的能量，并由下式给出：

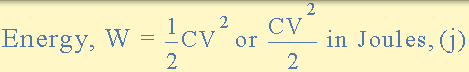
所以存储在上述 100uF 电容器电路中的能量计算如下：

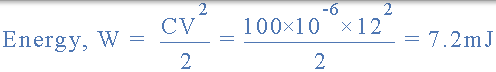
在我们关于电容器的部分的下一个教程中，我们看一下电容器颜色代码，并看到电容器的电容和电压值标记在其主体上的不同方式。