串联电容器

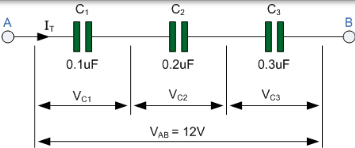
当电容器以链形式连接在一起时，电容器串联连接在一起

对于串联电容器，流过电容器的充电电流 iC 对于所有电容器都是相同的，因为它只有一条路径可供使用。

然后，串联的电容器都有相同的电流流过它们，因为 iT = i1 = i2 = i3 等。因此，无论电容如何，每个电容器都会在其板上存储相同数量的电荷 Q. 这是因为由任何一个电容器的板存储的电荷必须来自其相邻电容器的极板。因此，串联连接在一起的电容器必须具有相同的电荷。

QT = Q1 = Q2 = Q3 …等

考虑以下电路，其中三个电容器 C1，C2 和 C3 在点 A 和 B 之间的电源电压上以串联支路连接在一起。

串联连接中的电容器

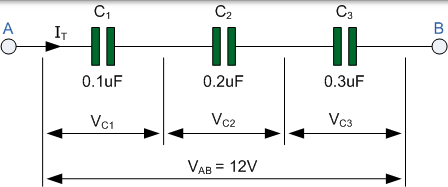
在之前的并联电路中，我们看到电路的总电容 CT 等于加在一起的所有单个电容的总和。然而，在串联电路中，以不同方式计算总电容或等效电容 CT.

在第一电容器的右手板上方的串联电路中，C1 连接到第二电容器 C2 的左手板，其右手板连接到第三电容器 C3 的左手板。然后，该串联连接意味着在 DC 电路中，电容器 C2 有效地与电路隔离。

结果是有效板面积减小到串联链中连接的最小单个电容。因此，每个电容器上的电压降将根据各个电容的值而不同。

然后通过将基尔霍夫电压定律（ KVL）应用于上述电路，我们得到：

由于 Q = C * V 并且重新排列为 V = Q / C，在上述 KVL 方程中用 Q / C 代替每个电容器电压 VC 将给出：

将每项除以 Q 后会得出，

串联电容器方程

将串联电容器串联起来时，各个电容器的倒数（ 1 / C）都加在一起（就像电阻并联）而不是电容本身。然后，串联电容器的总值等于各个电容的倒数之和的倒数。

电容器串联示例 No1

从上面的例子中得到三个电容值，我们可以计算三个电容器的总电容 CT，如下：

要记住的是，在串联配置连接在一起的电容器，其中一个重要的一点是，总电路的电容（ CT 任何数量的串联连接在一起的电容器的）总是比串联电容中最小的电容器还小，在上面的示例中，CT =0.055μF，串联链中最小电容的值仅为 0.1μF。

该倒数计算方法可用于计算在单个串联网络中连接在一起的任何数量的单个电容器。但是，如果只有两个串联电容器，那么可以使用更简单，更快速的计算等式，并如下所示：

如果两个串联连接的电容器相等且值相同，即： C1 = C2，我们可以进一步简化上述等式，以找到串联组合的总电容。

然后我们可以看到，当且仅当两个串联的电容器相同且相等时，则总电容 CT 将恰好等于电容值的一半，即： C/2。

对于串联电阻，串联电路上所有电压降的总和将等于施加电压 VS （基尔霍夫电压定律），对于串联电容也是如此。

对于串联电容器，由于电源频率，电容器的容抗作为阻抗。该容性电抗在每个电容器上产生电压降，因此串联电容器充当电容分压器网络。

结果是，应用于电阻器的分压器公式也可用于查找串联的两个电容器的各个电压。然后：

其中： CX 是所讨论的电容器的电容，VS 是串联链上的电源电压，VCX 是目标电容器两端的电压降。

电容器串联示例 No2

当连接到 12V 交流电源时，查找以下两组串联电容器的总电容和单个均方根电压降。

• a） 两个电容器，每个电容器的电容为 47nF
• b） 一个 470nF 的电容串联连接到 1μF 的电容

a） 总等容电容，

两个相同的 47nF 电容两端的电压降，

b） 不相等电容，

两个不相同的电容器上的电压降： C1 = 470nF，C2 =1μF。

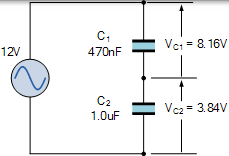
由于基尔霍夫电压定律适用于该电路和每个串联电路，因此各个电压降的总和将等于电源电压 VS 的值。然后 8.16 + 3.84 = 12V。

另请注意，如果电容值相同，在我们的第一个示例中为 47nF，则电源电压将在每个电容上均等分配，如图所示。这是因为串联链中的每个电容器共享相等且精确的电荷量（ Q = C x V =0.564μC），因此具有施加电压 VS 的一半（或多于两个电容器的百分比） 。

然而，当串联电容器值不同时，较大值的电容器将自身充电至较低电压而较小值电容器充电至较高电压，并且在上面的第二示例中，其分别显示为 3.84 和 8.16 伏。这种电压差允许电容器在每个电容器的极板上保持相同的电荷量 Q，如图所示。

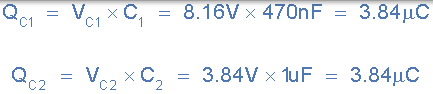
注意，串联连接的两个电容器上的电压降的比率将始终保持不变，无论电源频率如何，它们的电抗，XC 将保持成比例相同。

然后，即使供电频率从 100Hz 增加到 100kHz，我们示例中的两个 8.16 伏和 3.84 伏的电压降也将保持不变。

虽然每个电容器上的电压降对于不同的电容值将是不同的，但是板上的库仑电荷将是相等的，因为在整个串联电路中存在相同量的电流，因为所有电容器被提供相同数量或数量的电容器。电子

换句话说，如果每个电容器板上的电荷相同，则 Q 是恒定的，那么随着其电容减小，电容器板上的电压降增加，因为电荷相对于电容是大的。同样，较大的电容将导致其板上的电压降较小，因为电荷相对于电容较小。

电容器串联摘要

总而言之，包含串联电容器的电路的总电容或等效电容 CT 是加在一起的所有单个电容的倒数之和的倒数。

串联连接的电容器，所有的串联连接的电容器将具有相同的电流过它们，即 IT = I1 = I2 = I3。两个或更多个电容器串联的将总是具有跨越等量库仑电荷的他们的盘子。

作为电荷，（ Q）是相等且恒定的，电容器两端的电压降仅由电容器的值确定为 V = Q÷C。较小的电容值将导致较大的电压，而较大的电容值将导致较小的电压降。