RC 微分器

無源 RC 微分器是串聯的 RC 網路，其產生對應於微分的數學過程的輸出訊號。

對於無源 RC 微分電路，輸入連線到電容器，而輸出電壓來自與* RC 積分電路*完全相反的電阻。

無源 RC 微分器只不過是與電阻串聯的電容，這是一種頻率相關器件，它具有與固定電阻串聯的電抗（與積分器相反）。與積分電路一樣，輸出電壓取決於電路 RC 時間常數和輸入頻率。

因此，在低輸入頻率下，電容器的電抗 Xc 阻斷任何直流電壓或緩慢變化的輸入訊號。在高輸入頻率時，電容器電抗很低，允許快速變化的脈衝直接從輸入端傳遞到輸出端。

這是因為電容電抗（Xc）與電阻（R）的比率對於不同的頻率是不同的，頻率越低，輸出越少。因此，對於給定的時間常數，隨著輸入脈衝的頻率增加，輸出脈衝越來越像輸入脈衝的形狀。

我們在關於無源高通濾波器的教程中看到了這種效應，如果輸入訊號是正弦波，則** RC 微分器**將簡單地用作具有與 RC 對應的截止或轉角頻率的簡單高通濾波器（HPF），其串聯網路的時間常數（τ）。

因此，當用純正弦波饋電時，由於 Xc = 1 /（2πC）的標準電容電抗公式，RC 微分電路用作簡單的無源高通濾波器。

但是，也可以配置簡單的 RC 網路以執行輸入訊號的區分。我們從之前的教程中知道，通過電容器的電流是一個複數指數，由下式給出：iC = C（dVc / dt）。電容器充電（或放電）的速率與電阻量和電容量成正比，給出電路的時間常數。因此，RC 微分電路的時間常數是等於 R 和 C 的乘積的時間間隔。考慮下面的基本 RC 串聯電路。

RC 微分電路

對於 RC 微分器電路中，輸入訊號被施加到與該電阻兩端所採取的輸出的電容器的一側，則 V OUT 等於 V - [R。由於電容器是頻率相關元件，所以在板上建立的電荷量等於電流的時域積分。也就是說，電容器完全充電需要一定的時間，因為電容器不能瞬間充電，只能指數充電。

我們在關於* RC 積分器*的教程中看到，當單級電壓脈衝施加到 RC 積分器的輸入時，如果 RC 時間常數足夠長，則輸出變為鋸齒波形。RC 微分器也將改變輸入波形，但與積分器的方式不同。

電阻器電壓

我們之前說過，對於 RC 微分器，輸出等於電阻兩端的電壓，即：V OUT 等於 V R 並且是電阻，輸出電壓可以瞬間改變。

然而，電容器兩端的電壓不能立即改變，而是取決於電容 C 的值，因為它試圖在其板上儲存電荷 Q. 然後電流流入電容器，即我噸取決於在其板上的電荷的變化的速率。因此，電容器電流與電壓不成比例，而是與其時間變化成比例，給出：i = dQ / dt。

當電容器板上的電荷量等於 Q = C x Vc，即電容乘以電壓時，我們可以推匯出電容器電流的等式：

電容器電流

因此，電容器電流可寫為：

由於 VOUT等於 VR，其中根據歐姆定律的 VR也等於：iR x R。流過電容器的電流也必須流過電阻，因為它們都串聯連線在一起。從而：

因此，RC 微分電路的標準公式為：

RC 微分公式

然後，我們可以看出，輸出電壓 VOUT 是輸入電壓 VIN的導數，由 RC 的常數進行加權。其中 RC 表示串聯電路的時間常數 τ。

單脈衝 RC 微分器

當單個步進電壓脈衝首先施加到 RC 微分器的輸入時，電容器“最初出現”為快速變化訊號的短路。這是因為方波的正向邊緣的斜率 dv/dt 非常大（理想地是無限的），因此在訊號出現的瞬間，所有輸入電壓都通過電阻器上出現的輸出。

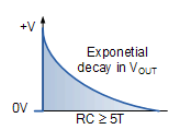
在輸入訊號的初始正向邊沿經過並且輸入的峰值恆定後，電容器開始以正常方式通過電阻器響應輸入脈衝以 RC 時間確定的速率充電常數，τ= RC。

隨著電容器充電，電阻器兩端的電壓以及輸出電壓以指數方式降低，直到電容器在 5RC（5T）的時間常數後變為完全充電，導致電阻器兩端的輸出為零。因此，完全充電電容器兩端的電壓等於輸入脈衝的值，如下：VC = VIN，只要輸入脈衝的幅度不變，該條件就成立。

如果現在輸入脈衝改變並返回到零，則脈衝的負向邊緣的變化率通過電容器到達輸出，因為電容器不能響應這種高 dv/dt 變化，結果是輸出端出現負增長。

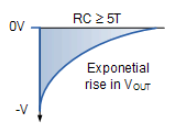
在輸入訊號的初始負向邊沿之後，電容器恢復並開始正常放電，電阻器兩端的輸出電壓以及輸出電壓隨著電容器放電而開始呈指數增加。

因此，無論何時輸入訊號快速變化，輸出端都會產生電壓尖峰，該電壓尖峰的極性取決於輸入是正向還是負向變化，因為正向產生正尖峰。輸入訊號的邊沿，以及由於負輸入訊號而產生的負尖峰。

因此，RC 微分器輸出實際上是輸入訊號的變化率的曲線圖，其與方波輸入波沒有相似之處，但是當輸入脈衝改變值時由窄的正和負尖峰組成。

通過改變方波輸入脈衝的時間週期 T 相對於串聯組合的固定 RC 時間常數，輸出脈衝的形狀將如圖所示改變。

RC 微分器輸出波形

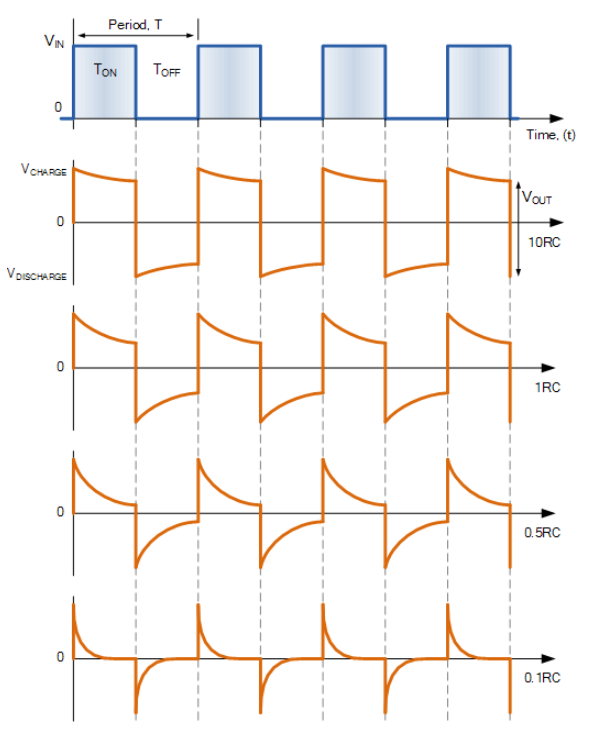
然後我們可以看到輸出波形的形狀取決於脈衝寬度與 RC 時間常數之比。當 RC 比脈衝寬度大得多（大於 10RC）時，輸出波形類似於輸入訊號的方波。當 RC 比脈衝寬度小得多（小於 0.1RC）時，輸出波形採用非常尖銳和窄的尖峰形式，如上所示。

因此，通過將電路的時間常數從 10RC 變為 0.1RC，我們可以產生一系列不同的波形。通常在 RC 微分電路中總是使用較小的時間常數，以在 R 上的輸出端提供良好的尖銳脈衝。因此，方波脈衝的差分（高 dv/dt 階躍輸入）是無限短的尖峰，導致 RC 微分電路。

假設方波波形的週期 T 為 20ms，脈衝寬度為 10ms（20ms 除以 2）。為使尖峰放電至其初始值的 37％，脈衝寬度必須等於 RC 時間常數，即 RC = 10ms。如果我們選擇電容值 C，1uF，那麼 R 等於 10kΩ。

為了使輸出類似於輸入，我們需要 RC 為脈衝寬度值的十倍（10RC），因此對於電容值，例如 1uF，這將給出一個 100kΩ 的電阻值。同樣，為了使輸出類似於尖銳脈衝，我們需要 RC 為脈衝寬度的十分之一（0.1RC），因此對於相同的電容值 1uF，這將給出一個電阻值：1kΩ，依此類推。

RC 微分器示例

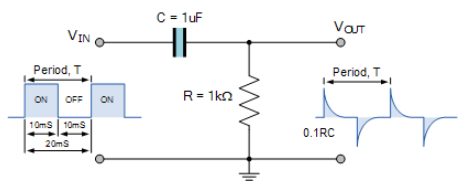
因此，通過將 RC 值設定為脈衝寬度的十分之一（並且在我們的示例中，這是 0.1 x 10ms = 1ms）或更低，我們可以在輸出端產生所需的尖峰，並且給定脈衝寬度的 RC 時間常數越低，尖峰更尖銳。因此，輸出波形的確切形狀取決於 RC 時間常數的值。

RC 微分器摘要

我們在此** RC 差分器**教程中已經看到，輸入訊號被施加到電容器的一側，輸出通過電阻器獲得。微分電路用於產生用於定時電路應用的觸發或尖峰型別脈衝。

當方波步進輸入應用於該 RC 電路時，它在輸出端產生完全不同的波形。輸出波形的形狀取決於輸入方波的週期時間 T（也可以說是頻率 f）和電路的 RC 時間常數值。

當輸入波形的週期時間也類似於或者比電路 RC 時間常數（更高頻率）更短時，輸出波形類似於輸入波形，即方波輪廓。當輸入波形的週期時間遠長於（較低頻率）電路 RC 時間常數時，輸出波形類似於窄的正和負尖峰。

輸出的正尖峰由輸入方波的前沿產生，而輸出的負尖峰由輸入方波的下降沿產生。然後 RC 微分電路的輸出取決於輸入電壓的變化率，因為效果非常類似於微分數學函式。