RC 放電電路
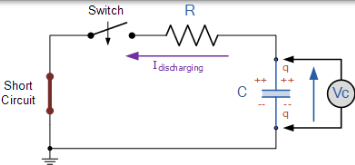
當從完全充電的 RC 電路中移除電壓源時,電容器 C 將通過電阻 R 放電。
在之前的RC 充電電路教程中,我們看到了電容器 C 如何通過電阻充電,直到達到等於 5 個時間常數或 5T 的時間,然後保持完全充電狀態。
如果這個完全充電的電容器現在與其 DC 電池電源電壓斷開,它將無限期地儲存其在充電過程中產生的能量(假設一個理想的電容器並忽略任何內部損耗),保持其端子上的電壓恆定。
如果現在拆下電池並用短路代替,當開關再次閉合時,電容器會通過電阻器 R 自身放電,因為我們現在有一個 RC 放電電路。當電容器通過串聯電阻器放電時,電容器內部儲存的能量被提取,電容器兩端的電壓 Vc 衰減到零,如下所示。
RC 放電電路
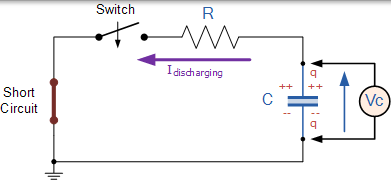
與之前的 RC 充電電路一樣,在 RC 放電電路中,時間常數( τ)仍然等於 63% 的值。然後,對於最初完全充電的 RC 放電電路,在一個時間常數 1T 之後電容器兩端的電壓下降了其初始值的 63% ,即其初始值的 1-0.63 = 0.37 或 37% 。
電路的時間常數是電容器放電至其完全充電值的 37% 以內所需的時間。因此,對於 RC 電阻電路,給出一個時間常數,即電路板上的電壓代表其最終值的 37%,即零伏特(完全放電),在我們的曲線中,這給出為 0.37Vs。
隨著電容器放電,它以不斷下降的速率失去電荷。在放電電路的初始條件開始時,是 T = 0,I = 0 和 q = Q。跨電容器板的電壓等於電源電壓, Vc = Vs。當板上的電壓處於其最高值時,最大放電電流在電路周圍流動。
RC 放電電路曲線
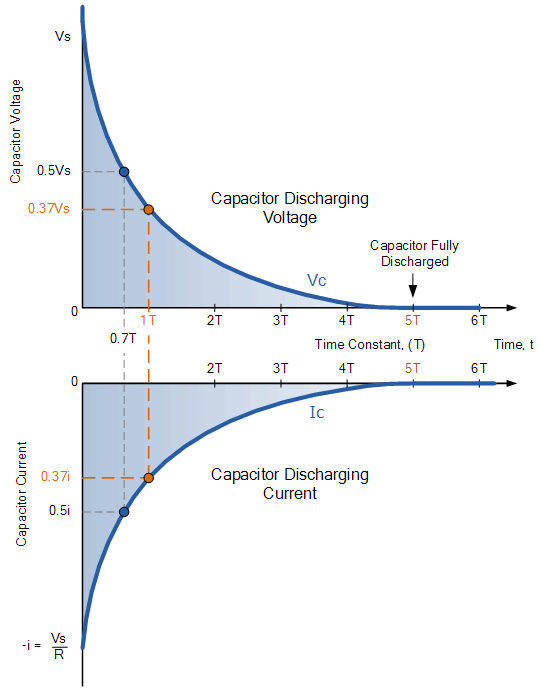
當開關閉合時,電容器現在開始放電,如圖所示,RC 放電曲線的衰減在開始時更陡峭,因為放電速率在開始時最快,然後隨著電容器以較慢的速率失去電荷而逐漸減小。隨著放電繼續,Vc 下降,放電電流減少。
與前面的充電電路一樣,電容器兩端的電壓 C 在 0.7T 時等於 0.5Vc,穩態完全放電值最終達到 5T。
對於 RC 放電電路,放電期間電容器兩端的電壓( Vc)隨時間的變化定義為:
其中,
- Vc 是電容兩端的電壓
- Vs 是電源電壓
- t 是自電源電壓消除後經過的時間
- RC 是 RC 放電電路的時間常數
就像之前的 RC 充電電路一樣,我們可以說在 RC 放電電路中,電容器將自身放電到一個時間常數所需的時間如下:
其中,R 的單位是 Ω,C 單位是法拉。
然後我們可以在下表中顯示給定時間常數下 RC 放電電路中電容器的百分比電壓和電流值。
RC 放電時間對照表
| 時間 | RC 值 | 電壓 | 電流 |
|---|---|---|---|
| 0.5τ | 0.5T = 0.5RC | 60.7% | 39.3% |
| 0.7τ | 0.7T = 0.7RC | 49.7% | 50.3% |
| 1.0τ | 1T = 1RC | 36.6% | 63.4% |
| 2.0τ | 2T = 2RC | 13.5% | 86.5% |
| 3.0τ | 3T = 3RC | 5.0% | 95.0% |
| 4.0τ | 4T = 4RC | 1.8% | 98.2% |
| 5.0τ | 5T = 5RC | 0.7% | 99.3% |
注意,由於 RC 放電電路的放電曲線是指數的,出於所有實際目的,在五個時間常數之後,電容器被認為是完全放電的。
因此,RC 電路的時間常數是衡量其充電或放電速度的指標。
RC 放電電路示例 No1
電容器充滿電至 10 伏。當開關閉合時,計算 RC 放電電路的 RC 時間常數 τ。
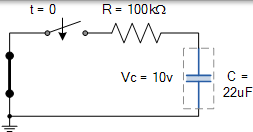
時間常數 τ 使用公式 T = R * C 以秒為單位求得。
因此,時間常數 τ 給出為:T = R * C = 100k×22uF = 2.2 秒
a) 0.7 時間常數下電容兩端的電壓是多少?
在 0.7 時間常數( 0.7T)Vc = 0.5Vc。因此,Vc = 0.5×10V = 5V
b) 1 個時間常數後,電容兩端的電壓是多少?
在 1 時間常數( 1T)Vc = 0.37Vc。因此,Vc = 0.37×10V = 3.7V
c) 電容器自身“完全放電”需要多長時間(等於 5 個時間常數)
1 時間常數( 1T)= 2.2 秒。因此,5T = 5×2.2 = 11 秒