RC 充電電路
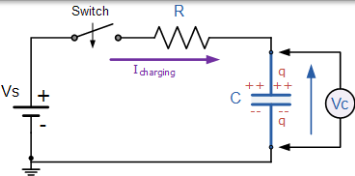
當電壓源施加到 RC 電路時,電容器 C 通過電阻 R 充電。
當向其施加直流(DC)或交流(AC)的訊號或電壓時,所有電氣或電子電路或系統在其輸入和輸出之間有某種形式的“時間延遲”。
該延遲通常被稱為電路的時間延遲或時間常數,並且是當首次施加階躍電壓或訊號時電路的時間響應。任何電子電路或系統的合成時間常數將主要取決於電容或電感連線的無功分量,並以 τ 為單位測量響應時間。
當 DC 電壓施加到電容器 ,電容器吸收充電電流來充電,並且當電壓降低時,電容器以相反的方向放電。由於電容器能夠儲存電能,因此它們就像小電池一樣,可以根據需要儲存或釋放能量。
電容器極板上的電荷如下: Q = CV。電容器能量的充電(儲存)和放電(釋放)永遠不會立即發生,但需要一定的時間,電容器充電或放電所需的時間在其最大電源值的一定百分比內,這被稱為它的時間常數 ( τ)。
如果電阻器與形成 RC 電路的電容器串聯連線,則電容器將逐漸通過電阻器充電,直到電容器兩端的電壓達到電源電壓。時間也稱為瞬態響應,電容器完全充電所需的時間相當於約 5 個時間常數或 5T。
該瞬態響應時間 T 以 τ = R×C (以秒為單位)來測量,其中 R 是以歐姆為單位的電阻器的值,C 是以法拉為單位的電容器的值。這就形成了 RC 充電電路的基礎,5T 也就是 5×RC 。
RC 充電電路
下圖顯示了一個電容器 C 與一個電阻 R 串聯形成一個 RC 充電電路,通過機械開關連線在直流電池電源( Vs)上。當開關閉合時,電容器將逐漸通過電阻器充電,直到其兩端的電壓達到電池的電源電壓。電容器充電的方式也如下所示。
RC 充電電路
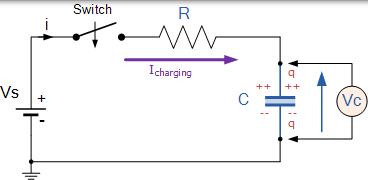
我們在上面假設,電容器 C 完全“放電”並且開關(S)完全開啟。這些是電路的初始條件,然後 t = 0,i = 0 和 q = 0。當開關閉合時,時間從 t = 0 開始,電流開始通過電阻流入電容器。
由於電容器兩端的初始電壓為零,( Vc = 0),電容器似乎是外部電路的短路,並且最大電流流過僅受電阻器 R 限制的電路。然後通過使用基爾霍夫電壓定律(KVL),電路周圍的電壓降如下:
現在的當前周圍電路中流動被稱為充電電流,通過歐姆定律可以計算出: I = Vs / R。
RC 充電電路曲線
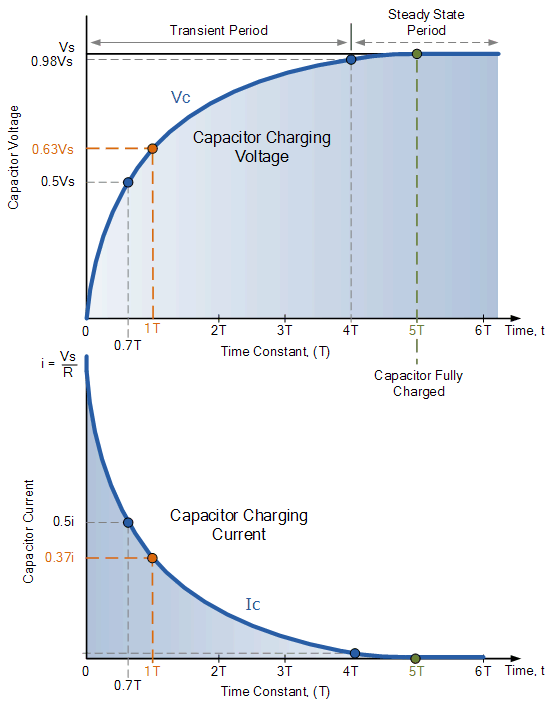
電容器現在開始充電,如圖所示,RC 充電曲線的上升在開始時更陡峭,因為充電速率在開始時最快,然後隨著電容器以較慢的速率進行額外充電而逐漸減小。
隨著電容器充電,其電路板上的電位差逐漸增加,電容器上的電荷達到其最大可能電壓的 63% 所需的實際時間(在我們的曲線中 0.63V)被稱為一個時間常數 T。
該 0.63Vs 電壓點的縮寫為 1T (一個時間常數)。
電容器繼續充電向上 Vs 和 Vc 之間的電壓差一直在降低。然後在其最終條件下,當電容器被稱為完全充電時,大於五個時間常數(5T),t = ∞,i = 0,q = Q = CV。然後在無窮大處電流減小到零,電容器就像開路狀態一樣,電壓降完全在電容器兩端。
從數學上講,我們可以說電容器充電到一個時間常數 1T 所需的時間如下:
RC 時間常數 τ
該 RC 時間常數僅指定電荷率,其中 R 單位為 Ω,C 的單位為法拉。
由於電壓 V 與由等式給出的電容器上的電荷相關,Vc = Q / C,在充電期間的任何時刻電容兩端的電壓( Vc)上的電壓如下所示:
其中
- Vc 是電容兩端的電壓
- Vs 是電源電壓
- t 是自施加電源電壓起經過的時間
- RC 是 RC 充電電路的時間常數
在相當於 4 個時間常數( 4T)的時間段之後,該 RC 充電電路中的電容器幾乎完全充電,電容器兩端的電壓現在約為其最大值的 98%,即 0.98Vs。電容器達到 4T 點所需的時間稱為瞬態週期。
在 5T 的時間之後,電容器現在被完全充電,並且電容器兩端的電壓( Vc)等於電源電壓( Vs)。當電容器充滿電時,電路中不再有電流流過。該 5T 點之後的時間段稱為穩態時間段。
然後我們可以在下表中顯示給定時間常數下 RC 充電電路中電容器的百分比電壓和電流值。
RC 充電對照表
| 時間 | RC 值 | 電壓 | 電流 |
|---|---|---|---|
| 0.5 τ | 0.5T = 0.5RC | 39.3% | 60.7% |
| 0.7 τ | 0.7T = 0.7RC | 50.3% | 49.7% |
| 1.0 τ | 1T = 1RC | 63.2% | 36.8% |
| 2.0 τ | 2T = 2RC | 86.5% | 13.5% |
| 3.0 τ | 3T = 3RC | 95.0% | 5.0% |
| 4.0 τ | 4T = 4RC | 98.2% | 1.8% |
| 5.0 τ | 5T = 5RC | 99.3% | 0.7% |
注意,由於 RC 充電電路的充電曲線是指數的,實際上電容器由於儲存在電容器中的能量而永遠不會變為 100%完全充電。因此,出於所有實際目的,在五個時間常數之後,電容器被認為是完全充電的。
由於電容器 Vc 兩端的電壓隨時間變化,並且在每個時間常數達到 5T 時是不同的值,我們可以在任何給定點計算電容器電壓 Vc 的值,例如。
RC 充電電路示例 No1
計算以下電路的 RC 時間常數 τ。
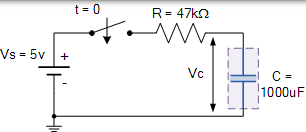
使用公式 T = R x C (秒)找到時間常數 τ。
因此,時間常數 τ 給出為: T = R x C = 47k×1000uF = 47 秒
a) 0.7 時間常數下電容兩端的電壓是多少?
在 0.7 時間常數( 0.7T)Vc = 0.5Vs。因此,Vc = 0.5×5V = 2.5V
b) 1 個時間常數下電容兩端的電壓值是多少?
在 1 時間常數( 1T)Vc = 0.63Vs。因此,Vc = 0.63×5V = 3.15V
c) 電容器完全充電需要多長時間?
電容器將以 5 個時間常數充滿電。
1 時間常數( 1T)= 47 秒,(從上面)。因此,5T = 5×47 = 235 秒
d) 100 秒後電容器兩端的電壓?
電壓公式為 Vc = V(1 - e-t/RC)
等於: Vc = 5(1-e-100/47) 從上面已知 RC = 47 秒,因此,Vc = 4.4 伏
我們已經看到電容器上的電荷由下式給出: Q = CV,並且當電壓首先施加到電容器的極板時,它以由其時間常數 τ 確定的速率充電。
在下一個教程中,我們將檢查放電電容器的電流 - 電壓關係,並在電容器板短接在一起時檢視與之相關的曲線。