無源低通濾波器

低通濾波器是一種電路，可用於修改，重塑或拒絕所有不需要的高頻電訊號，並接受或僅傳遞電路設計者所需的訊號。

換句話說，它們濾除不需要的訊號，理想濾波器將基於其頻率分離並傳遞正弦輸入訊號。在低頻應用（高達 100kHz）中，無源濾波器通常使用簡單的 RC （電阻 - 電容）網路構建，而高頻濾波器（100kHz 以上）通常由 RLC （電阻 - 電感 - 電容）元件構成。

無源濾波器由無源元件組成，如電阻，電容和電感，沒有放大元件（電晶體，運算放大器等），因此沒有訊號增益，因此它們的輸出電平始終小於輸入。

濾波器根據它們允許通過它們的訊號的頻率範圍來命名，同時阻擋或“衰減”其餘訊號。最常用的濾波器設計是：

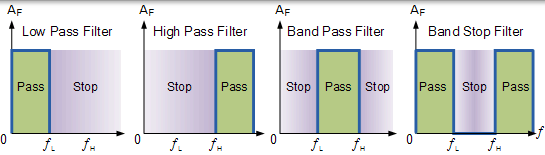
• 低通濾波器 - 低通濾波器只允許低頻訊號從 0Hz 到其截止頻率 ƒc 通過，同時阻止那些更高的頻率。
• 高通濾波器 - 高通濾波器僅允許高頻訊號從其截止頻率 ƒc 開始到無限高頻通過，同時阻止任何更低的訊號。
• 帶通濾波器 - 帶通濾波器允許在兩點之間設定的特定頻帶內的訊號通過，同時阻擋該頻帶兩側的較低和較高頻率。

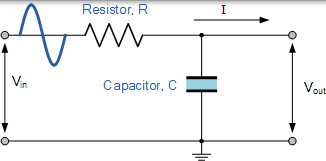
簡單的一階無源濾波器（一階）可以通過將單個電阻器和單個電容器串聯連線在一起，輸入訊號（VIN）與濾波器的輸出（VOUT ） 連線在一起。

根據我們將電阻器和電容器連線到輸出訊號的方式，決定了濾波器結構的型別，從而產生低通濾波器或高通濾波器。

由於任何濾波器的功能是允許給定頻帶的訊號不變地通過，同時衰減或弱化所有其他不需要的頻率，我們可以通過使用理想的頻率響應曲線來定義理想濾波器的幅度響應特性。四種基本濾波器型別如圖所示。

理想的濾波器響應曲線

濾波器可分為兩種不同的型別：有源濾波器和無源濾波器。有源濾波器包含放大裝置以增加訊號強度，而無源濾波器不包含放大裝置以增強訊號。由於無源濾波器設計中存在兩個無源分量，因此輸出訊號的幅度小於其對應的輸入訊號，因此無源 RC 濾波器衰減訊號並且增益小於 1。

低通濾波器可以是電容，電感或電阻的組合，旨在產生高於指定頻率的高衰減，並且在該頻率以下很少或沒有衰減。發生轉變的頻率稱為“截止”或“拐角”頻率。

最簡單的低通濾波器由電阻器和電容器組成，但更復雜的低通濾波器具有串聯電感器和並聯電容器的組合。在本教程中，我們將介紹最簡單的型別，無源雙元件 RC 低通濾波器。

低通濾波器

簡單的無源 RC 低通濾波器或 LPF 可以通過將單個電阻器與單個電容器串聯在一起而輕鬆製作，如下所示。在這種型別的濾波器佈置中，輸入訊號（VIN ）被施加到串聯組合（電阻器和電容器一起），但輸出訊號（VOUT ）僅在電容器上。

這種型別的濾波器通常稱為“一階濾波器”或“單極濾波器”，為什麼是一階或單極？，因為它在電路中只有“一個”無功分量即電容器。

RC 低通濾波器電路

如前面電容電抗教程中所述，電容的電抗與頻率成反比，而電阻值隨頻率的變化保持不變。在低頻時，與電阻器 R 的電阻值相比，電容器的容抗（XC ）將非常大。

這意味著電容器兩端的電壓電位 VC 將遠大於電阻器上產生的電壓降 VR. 在高頻時，反之亦然，VC 很小，並且由於容抗電容值的變化，VR 很大。

雖然上面的電路是 RC 低通濾波器電路，但它也可以被認為是一個頻率相關的可變分壓器電路，類似於我們在電阻器教程中看到的那樣。在該教程中，我們使用以下公式計算串聯連線的兩個單個電阻的輸出電壓。

$$ \mathrm { V } _ { \mathrm { out } } = \mathrm { V } _ { \mathrm { in } } \times \frac { \mathrm { R } _ { 2 } } { \mathrm { R } _ { 1 } + \mathrm { R } _ { 2 } } $$

我們也知道交流電路中電容器的容抗是：

$$ \mathrm { X } _ { \mathrm { C } } = \frac { 1 } { 2 \pi \mathrm { f } \mathrm { C } } \quad \mathrm { \Omega } $$

反向交流電路中的電流稱為阻抗，符號 Z，對於由單個電阻與單個電容串聯組成的串聯電路，電路阻抗計算如下：

$$ Z = \sqrt { R ^ { 2 } + X _ { C } ^ { 2 } } $$

然後通過將我們的等式中的阻抗代入電阻分壓器方程，我們得到：

RC 電勢分壓方程

$$ \mathrm { V } _ { \mathrm { out } } = \mathrm { V } _ { \mathrm { in } } \times \frac { \mathrm { X } _ { \mathrm { C } } } { \sqrt { \mathrm { R } ^ { 2 } + \mathrm { X } _ { \mathrm { C } } ^ { 2 } } } = \mathrm { V } _ { \mathrm { in } } \frac { \mathrm { X } _ { \mathrm { C } } } { \mathrm { Z } } $$

因此，通過使用串聯的兩個電阻器的分壓器方程並代替阻抗，我們可以計算任何給定頻率的 RC 濾波器的輸出電壓。

低通濾波器示例 No1

低通濾波器組成電路為，4.7 kΩ 電阻跟 47nF 的電容串聯，接到一個 10v 的正弦電源。計算頻率為 100Hz 時的輸出電壓（ VOUT ），然後再計算頻率為 10,000Hz 或 10kHz 時的情況。

電壓輸出頻率為 100Hz

$$ \mathrm { Xc } = \frac { 1 } { 2 \pi \mathrm { f } \mathrm { C } } = \frac { 1 } { 2 \pi \times 100 \times 47 \times 10 ^ { - 9 } } = 33,863 \Omega $$

$$ \mathrm { V } _ { \mathrm { ouT } } = \mathrm { V } _ { \mathrm { IN } } \times \frac { \mathrm { Xc } } { \sqrt { \mathrm { R } ^ { 2 } + \mathrm { X } _ { \mathrm { C } } ^ { 2 } } } = 10 \times \frac { 33863 } { \sqrt { 4700 ^ { 2 } + 33863 ^ { 2 } } } = 9.9 \mathrm { v } $$

電壓輸出頻率為 10,000Hz(10kHz)

$$ \mathrm { X } _ { \mathrm { c } } = \frac { 1 } { 2 \pi \mathrm { f } \mathrm { C } } = \frac { 1 } { 2 \pi \times 10,000 \times 47 \times 10 ^ { - 9 } } = 338.6 \Omega $$

$$ \mathrm { V } _ { \mathrm { ouT } } = \mathrm { V } _ { \mathrm { II } } \times \frac { \mathrm { X } _ { \mathrm { C } } } { \sqrt { \mathrm { R } ^ { 2 } + \mathrm { X } _ { \mathrm { C } } ^ { 2 } } } = 10 \times \frac { 338.6 } { \sqrt { 4700 ^ { 2 } + 338.6 ^ { 2 } } } = 0.718 \mathrm { v } $$

頻率響應

從上面的結果我們可以看出，當施加到 RC 網路的頻率從 100Hz 增加到 10kHz 時，電容上的電壓下降，電路的輸出電壓（ VOUT ）從 9.9v 降低到 0.718v。

通過將網路輸出電壓繪製成不同的輸入頻率值，可以找到低通濾波器電路的頻率響應曲線或波德圖功能，如下所示。

一階低通濾波器的頻率響應

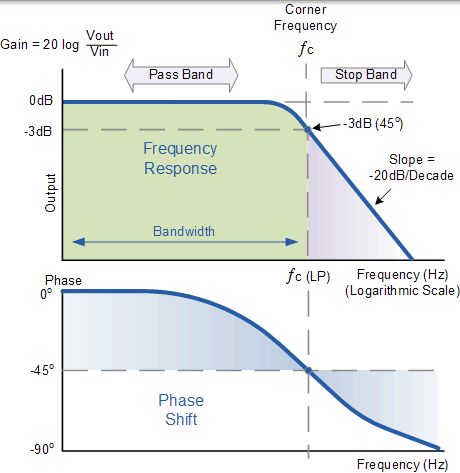
波特圖顯示濾波器的頻率響應對於低頻幾乎是平坦的，並且所有輸入訊號都直接傳遞到輸出，導致增益接近 1，稱為單位響應，直到達到其截止頻率點（ ƒc ）。這是因為電容器的電抗在低頻時很高，並阻止任何電流流過電容器。

在該截止頻率點之後，電路的響應在 -20dB / Decade 或（-6dB / Octave）“滾降” 的斜率下減小到零。請注意，對於任何 RC 組合，斜率的角度，此 -20dB / Decade 滾降斜率將始終相同。

在該截止頻率點之上施加到低通濾波器電路的任何高頻訊號將變得極大地衰減，即它們迅速減小。發生這種情況是因為在非常高的頻率下，電容器的電抗變得很低，以至於它在輸出端子上產生短路條件的效果，導致零輸出。

然後通過仔細選擇正確的電阻 - 電容組合，我們可以建立一個 RC 電路，允許低於某個值的頻率範圍通過電路不受影響，同時應用於該截止點​以上的電路的任何頻率都會衰減，這就是低通濾波器。

對於這種型別的低通濾波器電路，低於此截止頻率的所有頻率，ƒc 點在未衰減很小或沒有衰減的情況下被稱為濾波器通帶區域。該通帶區域也表示濾波器的頻寬。高於該點截止點的任何訊號頻率通常被稱為在濾波器阻帶區域中，並且它們將被大大衰減。

該截止，拐角或斷點頻率被定義為容抗和電阻相等的頻率點，R = Xc =4.7kΩ。發生這種情況時，輸出訊號衰減到輸入訊號值的 70.7% 或輸入的 -3dB （20 log（Vout / Vin））。雖然 R = Xc，但輸出不是輸入訊號的一半。這是因為它等於兩者的向量和，因此是輸入的 0.707。

作為濾波器包含一個電容器，輸出訊號的相位角 Φ 滯後於輸入訊號，並在 -3dB 截止頻率時，有 -45o 的相位滯後。這是由於在輸入電壓變化時對電容器極板充電所花費的時間，導致輸出電壓（電容器兩端的電壓）落後於輸入訊號的電壓。施加到濾波器的輸入頻率越高，電容器滯後越多，電路變得越來越異相。

截止頻率點和相移角可以通過以下等式找到：

截止頻率和相移

$$ { f \mathrm { c } = \frac { 1 } { 2 \pi \mathrm { RC } } = \frac { 1 } { 2 \pi \times 4700 \times 47 \times 10 ^ { - 9 } } = 720 \mathrm { Hz } }
$$

$$ { \text { Phase Shift } \varphi = - \arctan ( 2 \pi f \mathrm { RC } ) } $$

然後我們一上面例子中的低通濾波器電路中，截止頻率（ ƒc ）為 720Hz，此時輸出電壓為輸入電壓值 70.7%，輸出電壓有一個相移角 -45o。

二階低通濾波器

到目前為止，我們已經看到，通過將單個電阻器與單個電容器串聯連線，可以得到簡單的一階 RC 低通濾波器。該單極配置為我們提供了截止點以上的頻率的 -20dB /Decade 的衰減的滾降斜率 ƒ-3dB。然而，有時在濾波器電路中，斜率的 -20dB /decade（-6dB /octave）角度可能不足以去除不需要的訊號，因此可以使用兩級濾波，如圖所示。

二階低通濾波器

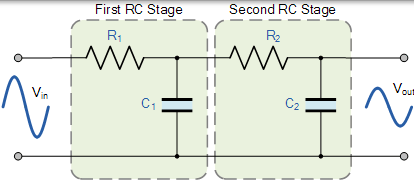
上述電路使用兩個無源一階低通濾波器連線或“級聯”在一起形成二階或兩極濾波器網路。因此，我們可以看到，通過簡單地向其新增額外的 RC 網路，可以將一階低通濾波器轉換為二階型別，並且我們新增的更多 RC 階段變為濾波器的階數。

如果很多（N）個 RC 電路級聯在一起，所得到的 RC 濾波電路將被稱為 N 階濾波器，其滾降斜率為 N x -20dB /decade。

因此，例如，二階濾波器的斜率為 -40dB / decade（-12dB /octave），四階濾波器的斜率為 -80dB / decade（-24dB /octave），依此類推。這意味著，隨著濾波器的階數增加，滾降斜率變得更陡峭，並且濾波器的實際阻帶響應接近其理想的阻帶特性。

第二階濾波器是很重要的，被廣泛應用於濾波器設計，因為當使用一階濾波器組合任何較高階次 n 階濾波器可以使用它們來設計。例如，通過將第一和第二低通濾波器串聯或級聯在一起來形成三階低通濾波器。

但是 RC 濾波器階段也存在一個缺點，儘管可以形成的濾波器的順序沒有限制，但隨著階數的增加，最終濾波器的增益和精度下降。

當相同的 RC 濾波器級級聯在一起時，在所需的截止頻率下的輸出增益相對於用作滾降斜率增加的濾波器級的數量減少（衰減）。我們可以使用以下公式定義所選截止頻率的衰減量。

ƒc 的無源低通濾波器增益

$$ \left( \frac { 1 } { \sqrt { 2 } } \right) ^ { n } $$

其中 n 是濾波器的階數。

因此對於二階無源低通濾波器，截至頻率 ƒc 的增益將等於 0.7071 x 0.7071 = 0.5Vin（-6dB），三階無源低通濾波器將等於 0.353Vin（-9dB），四階將為 0.25Vin（-12dB），依此類推。二階無源低通濾波器的轉角頻率 ƒc 由電阻/電容（RC）組合決定，並如下所示，

二階濾波器轉角頻率

$$ f _ { \mathrm { C } } = \frac { 1 } { 2 \pi \sqrt { \mathrm { R } _ { 1 } \mathrm { C } _ { 1 } \mathrm { R } _ { 2 } \mathrm { C } _ { 2 } } } \mathrm { Hz } $$

實際上，隨著濾波器級並因此其滾降斜率增加，低通濾波器 -3dB 轉角頻率點並且因此其通帶頻率從其上面的原始計算值改變由以下等式確定的量。

二階低通濾波器 -3dB 頻率

$$ f _ { ( - 3 d B ) } = f _ { c } \sqrt { 2 ^ { \frac { 1 } { n } } - 1 } $$

其中 ƒc 是所計算出的截止頻率，n 是濾波器階數，以及 ƒ-3dB 是新的 -3dB 通帶頻率，它是濾波器階數增加的結果。

然後假設相同的 -3dB 截止點的二階低通濾波器的頻率響應（波特圖）看起來像：

二階低通濾波器的頻率響應

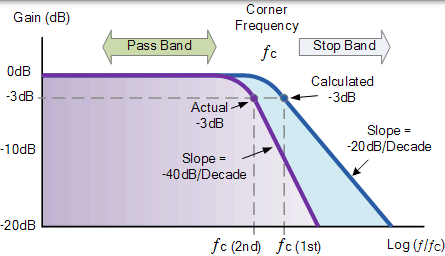
實際上，由於每個濾波器階數的動態阻抗影響其相鄰網路，因此難以精確地實現級聯無源濾波器以產生更大階濾波器。然而，為了降低負載效應，我們可以使每個後續級的阻抗是前一級的 10 倍多，因此 R2 = 10 x R1 和 C2 = 1/10 C1。二階及以上濾波器網路通常用於運算放大器的反饋電路中，來得到通常被稱為有源濾波器或 RC 振盪器電路中的相移網路。

低通濾波器摘要

因此，總結下，低通濾波器具有從 DC 開始一個恆定的輸出電壓，直到指定的截止頻率（ ƒC ）點。該截止頻率點是允許通過的電壓增益的 0.707 或 -3dB （dB = -20log * VOUT / IN ）。

當允許輸入訊號通濾波波器時，低於該截止點 fC 的頻率範圍通常稱為通帶。當輸入訊號被阻止或阻止通過時，該截止點“上方”的頻率範圍通常被稱為阻帶。

可以使用單個電阻器與輸入訊號 Vin 上的單個非極化電容器（或任何單個無功分量）串聯來製造簡單的一階低通濾波器，同時從電容器兩端獲取輸出訊號 Vout。

截止頻率或 -3dB 點，可使用標準公式 ƒc= 1 /(2πRC)找到。輸出訊號的相位角為 ƒc，對於低通濾波器為 -45o。

濾波器或任何濾波器的增益通常用分貝表示，並且是輸出值除以其相應輸入值的函式，並如下所示：

$$ \text {Gain in } d B = 20 \log \frac { V o u t } { V i n } $$

無源低通濾波器的應用在音訊放大器和揚聲器系統中，以將低頻低音訊號引導到較大的低音揚聲器或減少任何高頻噪聲或“嘶嘶聲”型別失真。當在音訊應用中像這樣使用時，低通濾波器有時被稱為“高切”或“高音切割”濾波器。

如果我們要反轉電路中電阻器和電容器的位置，以便現在從電阻器兩端獲取輸出電壓，我們將得到一個產生類似於高通濾波器的輸出頻率響應曲線的電路，以及這將在下一個教程中討論。

時間常數

到目前為止，我們一直對低通濾波器在受到正弦波形時的頻率響應感興趣。我們還看到濾波器的截止頻率（ƒc）是電路中電阻（R）和電容（C）相對於某個指定頻率點的乘積，通過改變兩個元件中的任何一個來改變這個截止頻率點可以通過增加它或減少它來實現。

我們還知道，由於在正弦波變化時對電容器充電然後放電所需的時間，電路的相移滯後於輸入訊號的相移。R 和 C 的這種組合在電容器上產生充電和放電效應，稱為電路的時間常數 （τ），如 RC 電路教程中所介紹的，為濾波器提供時域響應。

時間常數 τ 與截止頻率ƒc 有關：

$$ \tau = R C = \frac { 1 } { 2 \pi f c } $$

或以截止頻率 ƒc 來表示為：

$$ f _ { C } = \frac { 1 } { 2 \pi R C } \text { or } \frac { 1 } { 2 \pi \tau } $$

輸出電壓 VOUT 取決於時間常數和輸入訊號的頻率。隨著時間平滑變化的正弦訊號，電路表現為一個簡單的一階低通濾波器，如上所述。

但是，如果我們要將輸入訊號更改為具有幾乎垂直階躍輸入的方波形狀 ON/OFF 型別的訊號，那麼現在我們的濾波器電路會發生什麼。電路的輸出響應將發生顯著變化，併產生另一種通常稱為積分器的電路。

RC 積分器

該積分器基本上是一個低通濾波器電路在一個方波階躍響應輸入訊號轉換成作為電容器充電和放電的三角形狀的波形輸出的時域中操作。三角波形由交變但相等的正負斜坡訊號組成。

如下所示，如果 RC 時間常數與輸入波形的時間週期相比較長，則所得的輸出波形將是三角形的，並且輸入頻率越高，輸出幅度與輸入的輸出幅度相比越低。

RC 積分電路

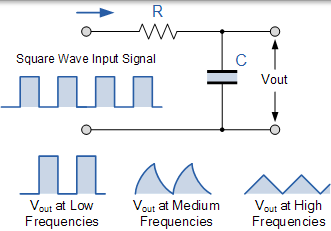
這使得這種型別的電路非常適合於將一種型別的電子訊號轉換成另一種型別的電子訊號，以用於波形發生或波形整形電路。