無源帶通濾波器

無源帶通濾波器可以通過將低通濾波器與高通濾波器連線在一起來實現。

帶通濾波器可用於隔離或濾除位於特定頻帶或頻率範圍內的某些頻率。使用與電容串聯的單個電阻可以精確控制 RC 無源濾波器中的截止頻率或 ƒc 點，並且根據它們連線的方式，我們已經得到低通或高通濾波器。

這些型別的無源濾波器的一個簡單用途是在音訊放大器應用或電路中，例如在揚聲器交叉濾波器或前置放大器音調控制中。有時必須僅通過一定範圍的頻率，這些頻率不是從 0Hz(DC) 開始，或是在某個高頻點處結束，而是在一定範圍或頻帶內，無論是窄還是寬。

通過將單通道低通濾波器電路與高通濾波器電路連線或“級聯”在一起，我們可以生產另一種型別的無源 RC 濾波器，它可以通過一個選定的範圍或“頻帶”頻率，可以是窄的也可以是寬的，同時衰減所有頻率超出此範圍的人。這種新型無源濾波器裝置產生頻率選擇濾波器，通常稱為帶通濾波器或簡稱 BPF。

帶通濾波器電路

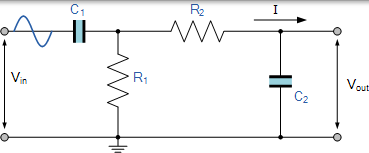
與僅傳遞低頻範圍訊號的低通濾波器或傳遞更高頻率範圍訊號的高通濾波器不同，帶通濾波器在頻率的某個頻帶範圍內傳遞訊號而不會使輸入失真訊號或引入額外的噪音。該頻帶可以是任何寬度，通常稱為濾波器頻寬。

頻寬通常定義為兩個指定頻率截止點 ƒc 之間存在的頻率範圍，即最大中心或共振峰值以下 3dB，同時衰減這兩個點之外的其他頻率。

頻寬為下截止頻率 ƒcLOWER 和上截止頻率 ƒcHIGHER 點。換句話說，BW =ƒH - ƒL。顯然，為使通帶濾波器正常工作，低通濾波器的截止頻率必須高於高通濾波器的截止頻率。

理想帶通濾波器還可用於隔離或濾除位於特定頻帶內的某些頻率，例如噪聲消除。帶通濾波器通常被稱為二階濾波器（兩極），因為它們在其電路設計中具有兩個無功元件，低通電路中有一個電容，高通電路中有另一個電容。

二階帶通濾波器的頻率響應

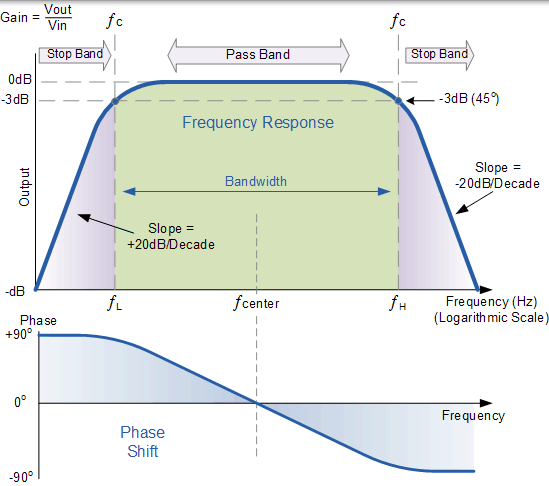
上面的波特圖或頻率響應曲線顯示了帶通濾波器的特性。在這裡，訊號在低頻衰減，輸出直到頻率達到下截止頻率 ƒL 處的以 +20dB/Decade (6dB/Octave) 的斜率增加。在此頻率時，輸出電壓為輸入訊號值的 1/√2= 70.7% 或輸入的 -3dB (20*log(VOUT/VIN))。

輸出繼續最大增益直到它到達上截止頻率點 ƒH，隨後隨著頻率的增加，以 -20dB/Decade (6dB/Octave) 斜率衰減。最大輸出增益點一般是上下截至頻率之間的兩條 -3dB 值的幾何平均值，它被稱為“中心頻率”或“共振峰值” ƒr。這種幾何平均值計算為 ƒr2 =ƒ(UPPER) x ƒ(LOWER)。

帶通濾波器是二階（兩極）型濾波器，因為它在其電路結構中具有“兩個”無功分量，那麼相位角將是先前看到的一階濾波器的兩倍，即180o。輸出訊號在到達中心或諧振頻率前超前輸入90o，在 ƒr 點時輸入輸出的相位差為 0o（同相），然後隨著輸出頻率的增加，輸出滯後輸入 90o。

可以使用低通濾波器和高通濾波器相同的公式找到帶通濾波器的上下截止頻率點，比如，

$$ f _ { C } = \frac { 1 } { 2 \pi R C } H z $$

然後，顯然，可以通過兩個濾波器的兩個截止頻率點的定位來控制濾波器的通頻寬度。

帶通濾波器示例 No1

使用 RC 元件構建二階帶通濾波器，僅允許頻率超過 1kHz 和低於 30kHz 的訊號通過。假設兩個電阻都是 10kΩ，計算所需的兩個電容的值。

高通濾波器階段

跟電阻值 10kΩ 一起來得到 1kHz 的截止頻率 ƒL 需要的電容值 C1，計算公式為：

$$ C _ { 1 } = \frac { 1 } { 2 \pi f _ { L } R } = \frac { 1 } { 2 \pi \times 1,000 \times 10,000 } = 15.9 n F $$

然後，高通階段得到 1.0kHz 的截止頻率所需的 R1 和 C1 的值為，R1 =10kΩ 以及最接近的電容優選值為 C1 = 15nF。

低通濾波器階段

跟電阻值 10kΩ 一起來得到 30kHz 的截止頻率 ƒL 需要的電容值 C2，計算公式為：

$$ C _ { 2 } = \frac { 1 } { 2 \pi f _ { H } R } = \frac { 1 } { 2 \pi \times 30,000 \times 10,000 } = 530 p F $$

然後，低通階段得到 30kHz 的截止頻率所需的 R2 和 C2 的值為，R =10kΩ 和 C = 530pF。但是，計算出的電容值 530pF 的最接近的優選值是 560pF，因此我們使用 560pF。

電阻 R1 和 R2 的值分別為 10kΩ，高通和低通濾波器的電容器 C1 和 C2 的兩個值分別為 15nF 和 560pF，那麼我們的簡單無源帶通濾波器電路如下所示，

完成帶通濾波器電路

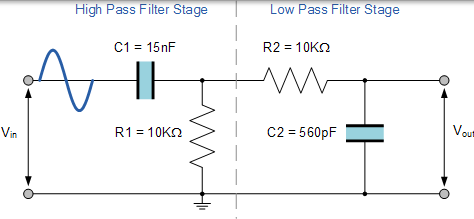
帶通濾波器諧振頻率

我們還可以計算帶通濾波器的“諧振”或“中心頻率” ƒr 點，輸出增益處於其最大值或峰值。該峰值不是你可能預期的上下 -3dB 截止點的算術平均值，但實際上是“幾何”或平均值。這種幾何平均值計算為 ƒr2 = ƒc(UPPER) x ƒc(LOWER) 例如：

中心頻率方程

$$ f r = \sqrt { f _ { L } x f _ { H } } $$

其中，

• ƒr 是諧振或中心頻率
• ƒL 是下 -3dB 截止頻率點
• ƒH 是上 -3db 截止頻率點

在我們的上面的簡單的示例中，該濾波器值的計算截止頻率是 ƒL = 1060 Hz 和 ƒH = 28420 Hz。

然後通過將這些值代入上面的等式給出中心共振頻率：

$$ f r = \sqrt { f _ { L } \times f _ { H } } = \sqrt { 1,060 \times 28,420 } = 5,48 k H z $$

帶通濾波器摘要

可以通過將單個低通濾波器與高通濾波器級聯在一起來製作簡單的無源帶通濾波器。RC 組合的低 -3dB 截止點和高 -3dB 截止點之間的頻率範圍稱為濾波器頻寬。

濾波器頻寬的寬度或頻率範圍可以非常小並且是選擇性的，或者非常寬但非選擇性，這取決於所使用的 R 和 C 的值。

中心或共振頻率點是下部和上部截止頻率的幾何平均值。在該中心頻率處，輸出訊號處於其最大值，並且輸出訊號的相移與輸入訊號相同。

來自帶通濾波器或任何無源 RC 濾波器的輸出訊號的幅度將始終小於輸入訊號的幅度。換句話說，無源濾波器也是衰減器，其電壓增益小於 1。為了提供電壓增益大於 1 的輸出訊號，在電路設計中需要某種形式的放大。

無源帶通濾波器被歸類為一個二階濾波器，因為它的設計中有兩個無源元件，即電容器。它由兩個單獨的 RC 濾波器電路組成，每個濾波器電路都是一階濾波器。

如果多個濾波器串聯在一起所產生的電路將被稱為 N 階濾波器，其中的 N 代表無源元件的數目，因此也是濾波器電路內的極數。例如，濾波器階數可以是 2 階，4 階，10 階等。

濾波器階數越高，斜率的陡峭度將是 -20dB/decade 的 N 倍。然而，通過將兩個或更多個單獨電容器組合在一起而形成的單個電容器值仍然是一個電容器。

我們上面的例子顯示了理想帶通濾波器的輸出頻率響應曲線，其中通帶具有恆定增益，阻帶中具有零增益。實際上，該帶通濾波器電路的頻率響應跟理想情況不同，因為高通電路的輸入電抗會影響低通電路（串聯或並聯連線的元件）的頻率響應，反之亦然。克服這種情況的一種方法是在兩個濾波器電路之間提供某種形式的電隔離，如下所示。

緩衝單個濾波階段

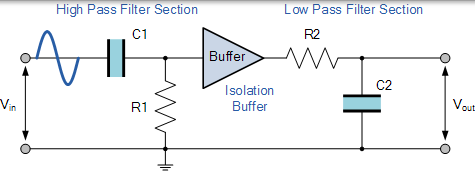
將放大和濾波組合到同一電路中的一種方法是使用運算放大器，這些例子在運算放大器部分有介紹。在下一個教程中，我們將研究在其設計中使用運算放大器的濾波器電路，不僅要引入增益，還要提供各級之間的隔離。這些型別的濾波器裝置通常稱為有源濾波器。