有源低通濾波器

通過將基本的 RC 低通濾波器電路與運算放大器相結合，我們可以建立一個有放大的有源低通濾波器電路

在 RC 無源濾波器教程中，我們看到了基本的一階濾波器電路，如低通濾波器和高通濾波器，只需使用一個串聯的電阻器與一個連線在正弦輸入訊號上的非極化電容器即可製成。

我們還注意到無源濾波器的主要缺點是輸出訊號的幅度小於輸入訊號的幅度，即增益絕不大於 1，並且負載阻抗會影響濾波器特性。

對於包含多級的無源濾波器電路，訊號的衰減幅度損失會變得非常嚴重。恢復或控制訊號損失的一種方法是通過使用有源濾波器進行放大。

顧名思義，有源濾波器在其電路設計中包含有源元件，如運算放大器、電晶體或 FET。它們從外部電源獲取電源，並使用它來增強或放大輸出訊號。

濾波器放大還可用於通過產生更具選擇性的輸出響應來對濾波器電路的頻率響應進行整形或改變，從而使濾波器的輸出頻寬更窄或更寬。那麼無源濾波器和有源濾波器之間的主要區別在於增益是否放大。

有源濾波器通常在其設計中使用運算放大器（op-amp），在運算放大器教程中，我們看到運算放大器具有高輸入阻抗，低輸出阻抗和由其內部的反饋迴路的電阻網路確定的電壓增益。

與理論上具有無限高頻響應的無源高通濾波器不同，有源濾波器的最大頻率響應限於所使用的運算放大器的增益/頻寬乘積（或開環增益）。儘管如此，有源濾波器通常比無源濾波器更容易設計，當使用良好的電路設計時，它們具有良好的效能特性，非常好的精度，陡峭的滾降和低噪聲。

有源低通濾波器

最常見且易於理解的有源濾波器是有源低通濾波器。其工作原理和頻率響應與之前看到的無源濾波器完全相同，這次唯一的區別是它使用運算放大器進行放大和增益控制。最簡單形式的低通有源濾波器是將反相或非反相放大器（如運算放大器教程中討論的相同）連線到基本 RC 低通濾波器電路，如圖所示。

一階低通濾波器

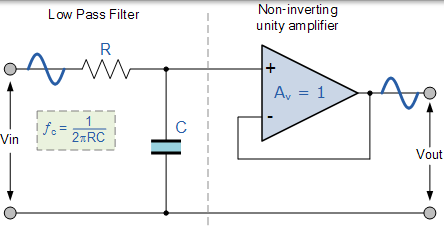
該一階低通有源濾波器僅由無源 RC 濾波器級組成，為非反相運算放大器的輸入提供低頻路徑。放大器配置為電壓跟隨器（緩衝器），其 DC 增益為 1，Av = +1 或單位增益，而不是之前的無源 RC 濾波器，其 DC 增益小於 1。

這種配置的優點是運算放大器的高輸入阻抗可防止濾波器輸出上的過載，同時其低輸出阻抗可防止濾波器截止頻率點受負載阻抗變化的影響。

雖然這種配置為濾波器提供了良好的穩定性，但其主要缺點是它沒有高於 1 的電壓增益。然而，雖然電壓增益是單位，但功率增益非常高，因為其輸出阻抗遠低於其輸入阻抗。如果需要大於 1 的電壓增益，我們可以使用以下濾波器電路。

具有放大功能的有源低通濾波器

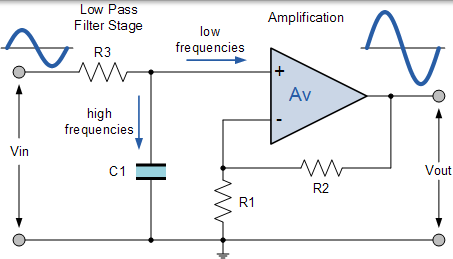
除了放大器的通帶增益 AF 增加輸出幅度外，電路的頻率響應與無源 RC 濾波器的頻率響應相同。對於非反相放大器電路，濾波器的電壓增益幅度等於反饋電阻（ R2 ）除以其相應的輸入電阻（ R1 ），如下所示：

$$ \mathrm { DC } \text { gain } = \left( 1 + \frac { \mathrm { R } _ { 2 } } { \mathrm { R } _ { 1 } } \right) $$

因此，作為頻率函式的有源低通濾波器的增益將是：

一階低通濾波器的增益

$$ \text { Voltage Gain, } ( A v ) = \frac { \text {Vout} } { V i n } = \frac { A _ { F } } { \sqrt { 1 + \left( \frac { f } { f c } \right) ^ { 2 } } } $$

其中，

• AF =濾波器的通帶增益（ 1 + R2 / R1 ）
• ƒ = 輸入訊號的頻率，單位為赫茲（Hz）
• ƒc =以赫茲為單位的截止頻率（Hz）

因此，可以從上面的頻率增益公式驗證低通有源濾波器的操作：

1. 在非常低的頻率下，ƒ<ƒc 時， $\frac { \mathrm { Vout } } { \mathrm { Vin } } \cong \mathrm { A } _ { \mathrm { F } }$
2. 在截止頻率，ƒ=ƒc 時， $\frac { Vout } { \operatorname { Vin } } = \frac { A _ { F } } { \sqrt { 2 } } = 0.707 \mathrm { A } _ { \mathrm { F } }$
3. 在非常高的頻率下，ƒ>ƒc 時， $ \frac { \text { Vout } } { \text { Vin } } < A _ { F } $

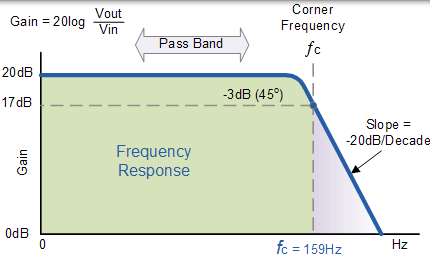
因此，有源低通濾波器具有從 0Hz 到截止點 ƒC 不變的增益 AF 。在 ƒC 增益為 0.707AF，在 ƒC 之後它隨著頻率的增加以恆定的速率下降。也就是說，當頻率增加 10 倍時，電壓增益減小為原來的 1/10。

換句話說，每當頻率增加 10 時，增益會降低 20dB= 20 * log(10)。當處理濾波器電路時，電路的通帶增益的幅度通常以分貝或 dB 表示為電壓增益的函式，定義如下：

電壓增益幅度（dB）

$$ \begin{array} { c } { \mathrm { AV } ( \mathrm { dB } ) = 20 \log _ { 10 } \left( \frac { \mathrm { Vout } } { \mathrm { Vin } } \right) } \\ { \therefore - 3 \mathrm { dB } = 20 \log _ { 10 } \left( 0.707 \frac { \mathrm { Vout } } { \mathrm { Vin } } \right) } \end{array} $$

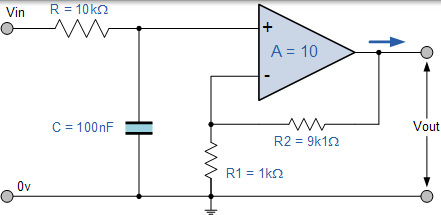
有源低通濾波器示例 No1

設計一種同相有源低通濾波器電路，其低頻增益為 10，高頻截止轉角頻率為 159Hz，輸入阻抗為 10KΩ。

非反相運算放大器的電壓增益如下：

$$ A _ { F } = 1 + \frac { R _ { 2 } } { R _ { 1 } } = 10 $$

假設電阻器 R1 的值為 1kΩ，重新排列上面的公式給出 R2 的值 ：

$$ R _ { 2 } = ( 10 - 1 ) x R _ { 1 } = 9 x | k \Omega = 9 k \Omega $$

然後，對於 10 倍的電壓增益，R1 =1kΩ，R2 =9kΩ。但是，不存在 9kΩ 電阻，因此使用下一個優選值 9k1Ω。

將此電壓增益轉換為分貝 dB 值可得出：

$$ \text {Gain in } d B = 20 \log A = 20 \log 10 = 20 d B $$

截止頻率（ ƒc ）為 159Hz，輸入阻抗為 10kΩ。可以使用以下公式計算截止頻率：

$$ f _ { C } = \frac { 1 } { 2 \pi R C } H z $$

其中，$f _ { C } = 159 \mathrm { Hz } ) $ and $ ( \mathrm { R } = 10 \mathrm { K } \Omega $

然後，通過重新排列上面的公式，我們可以找到電容器 C 的值 ：

$$ C = \frac { 1 } { 2 \pi f c R } = \frac { 1 } { 2 \pi x 159 \times 10 k \Omega } = 100 n F $$

然後，最終電路及其頻率響應如下：

低通濾波器電路

頻率響應曲線

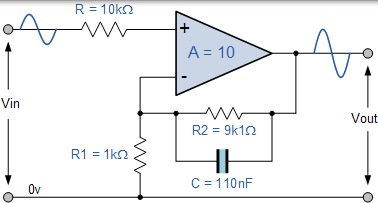
如果連線到電路輸入的外部阻抗發生變化，則此變化也會影響濾波器的轉角頻率（串聯或並聯連線的元件）。避免這種情況的一種方法是將電容器與反饋電阻器 R2 並聯。

考慮電阻值是 9k1Ω ，電容值將從 100nF 略微變化到 110nF，用於計算截止轉角頻率的公式與用於 RC 無源低通濾波器的公式相同。

$$ f _ { C } = \frac { 1 } { 2 \pi C R _ { 2 } } \text { Hertz } $$

有源低通濾波器電路的一個例子如下。

簡化的非反相放大器濾波電路

等效反相放大器濾波電路

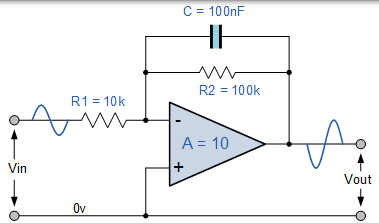
應用有源低通濾波器是在音訊放大器，均衡器或揚聲器系統向低頻低音訊號引導至較大的低音揚聲器或以減少任何高頻噪聲或“嘶嘶”型別的失真。當在音訊應用中使用這樣的時，有源低通濾波器有時被稱為“低音增強”濾波器。

二階低通有源濾波器

與無源濾波器一樣，只需在輸入路徑中使用額外的 RC 網路，即可將一階低通有源濾波器轉換為二階低通濾波器。二階低通濾波器的頻率響應與一階型別的頻率響應相同，不同之處在於阻帶衰減將是 的一階濾波器的兩倍 - 40dB/decade（12dB /octave）。因此，二階有源低通濾波器所需的設計步驟是相同的。

二階有源低通濾波器電路

當將濾波器電路級聯在一起以形成高階濾波器時，濾波器的總增益等於每級的乘積。例如，一級的增益可以是 10，第二級的增益可以是 32，第三級的增益可以是 100，然後總增益將是 32,000，（10 x 32 x 100），如下所示。

級聯電壓增益

$$ \begin{aligned} \mathrm { Av } & = \mathrm { Av } _ { 1 } \times \mathrm { Av } _ { 2 } \times \mathrm { AV } _ { 3 } \\ \mathrm { Av } ( \mathrm { dB } ) & = 20 \log _ { 10 } ( 32,000 ) \\ \mathrm { Av } ( \mathrm { dB } ) & = 90 \mathrm { d } \mathrm { B } \\ \mathrm { Av } ( \mathrm { dB } ) & = 90 d B \\ 90 \mathrm { d } \mathrm { B } & = 20 \mathrm { d } \mathrm { B } + 30 \mathrm { d } \mathrm { B } + 40 \mathrm { d } \mathrm { B } \end{aligned} $$

二階（兩極）有源濾波器很重要，因為可以使用它們設計高階濾波器。通過將一階和二階濾波器級聯在一起，可以構造具有奇數或甚至高達任何值的階數值的濾波器。在下一個關於濾波器的教程中，我們將看到有源高通濾波器可以通過反轉電路中電阻和電容的位置來構建。