有源高通濾波器

通過將無源 RC 濾波器網路與運算放大器組合以產生具有放大的高通濾波器,可以建立有源高通濾波器。
有源高通濾波器 (HPF) 的基本操作與其等效 RC 無源高通濾波器電路相同,不同之處在於該電路具有運算放大器包含在其設計中,提供放大和增益控制。
與之前的有源低通濾波器電路一樣,最簡單形式的有源高通濾波器是將標準反相或非反相運算放大器連線到基本 RC 高通無源濾波器電路,如圖所示。
一階高通濾波器
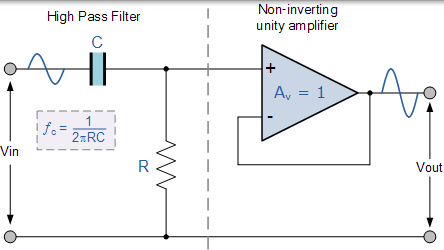
從技術上講,沒有有源高通濾波器這樣的東西。與具有“無限”頻率響應的無源高通濾波器不同,有源高通濾波器的最大通帶頻率響應受到所使用的運算放大器的開環特性或頻寬的限制,使得它們看起來好像是帶通濾波器,具有高頻截止頻率,由運算放大器和增益的選擇決定。
在運算放大器教程中,我們看到運算放大器的最大頻率響應僅限於增益/頻寬乘積或正在使用的運算放大器的開環電壓增益( AV ),從而使其具有頻寬限制,其中閉環運算放大器的響應與開環響應相交。
一個常用的運算放大器,如 uA741,具有典型的“開環”(無任何反饋),最大約 100dB 的直流電壓增益,隨著作為輸入頻率的增加增益以 -20dB / Decade(-6db / Octave)的滾降率降低。uA741 的增益降低,直到達到單位增益(0dB)或其交叉頻率 ƒt (約為 1MHz)。這使得運算放大器的頻率響應曲線與一階低通濾波器的頻率響應曲線非常相似,如下所示。
典型運算放大器的頻率響應曲線
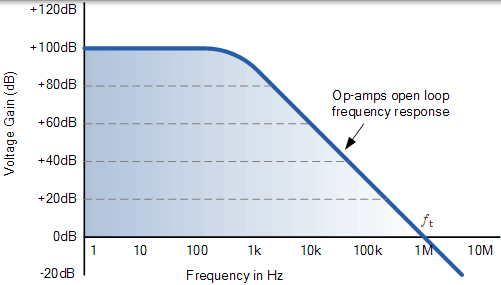
然後,高頻“高通濾波器”的效能受到該單位增益交叉頻率的限制,該交叉頻率決定了開環放大器的總頻寬。對於高速數字視訊放大器,運算放大器的增益頻寬積從大約 100kHz 開始,小訊號放大器高達約 1GHz,基於運算放大器的有源濾波器可以實現非常好的精度和效能,前提是低容差電阻器和電容器使用。
在正常情況下,閉環有源高通或帶通濾波器所需的最大通帶遠低於最大開環轉換頻率。但是,在設計有源濾波器電路時,為電路選擇正確的運算放大器非常重要,因為高頻訊號的丟失可能會導致訊號失真。
有源高通濾波器
顧名思義,一階(單極) 有源高通濾波器衰減低頻並傳遞高頻訊號。它僅由無源濾波器部分和非反相運算放大器組成。電路的頻率響應與無源濾波器的頻率響應相同,不同之處在於訊號的幅度通過放大器的增益增加,而對於非反相放大器,通帶電壓增益的值為 1 + R2 / R1,與低通濾波器電路相同。
具有放大功能的有源高通濾波器
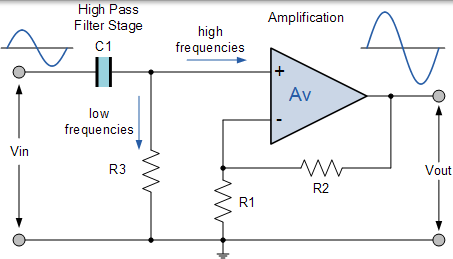
一階高通濾波器僅由無源濾波器和非反相放大器組成。除了通過放大器的增益增加訊號的幅度之外,電路的頻率響應與無源濾波器的頻率響應相同。
對於非反相放大器電路,濾波器的電壓增益幅度作為反饋電阻( R2 )除以其相應的輸入電阻( R1 )的函式給出,並如下所示:
增益有源高通濾波器
$$ \text { Voltage Gain, } ( \mathrm { Av } ) = \frac { \mathrm { Vout } } { \mathrm { Vin } } = \frac { \mathrm { A } _ { \mathrm { F } } \left( \frac { f } { f \mathrm { c } } \right) } { \sqrt { 1 + \left( \frac { f } { f \mathrm { c } } \right) ^ { 2 } } } $$
其中,
- AF =濾波器的通帶增益,( 1 + R2 / R1 )
- ƒ = 輸入訊號的頻率,單位為赫茲,(Hz)
- ƒc = 以赫茲為單位的截止頻率,(Hz)
就像低通濾波器一樣,高通有源濾波器的工作可以從上面的頻率增益公式中驗證:
- 在非常低的頻率下,ƒ < ƒc 時,$\frac { \mathrm { Vout } } { \mathrm { Vin } } < \mathrm { A } _ { \mathrm { F } }$
- 在截止頻率,ƒ = ƒc 時,$\frac { ) Vout ( } { V ) in ( } = \frac { A _ { F } } { \sqrt { 2 } } = 0.707 \mathrm { A } _ { \mathrm { F } }$
- 在非常高的頻率下,ƒ > ƒc 時, \frac { \mathrm { Vout } } { \mathrm { Vin } } \cong \mathrm { A } _ { \mathrm { F } }
然後,有源高通濾波器增益 AF 從 0Hz 增加到低頻截止點 ƒC,隨著頻率的增加以 20dB /decade 增加。在 ƒC 處,增益是 0.707 * AF, ƒC 之後的所有頻率都是通帶頻率,從而濾波器具有恆定的增益 AF, 最高頻率由運算放大器的閉環頻寬決定。
在處理濾波器電路時,電路通帶增益的幅度通常以分貝或 dB 表示,作為電壓增益的函式,這被定義為:
電壓增益幅度(dB)
$$ \begin{array} { c } { \mathrm { Av } ( \mathrm { dB } ) = 20 \log _ { 10 } \left( \frac { \mathrm { Vout } } { \mathrm { Vout } } \right) } \\ { \therefore - 3 \mathrm { dB } = 20 \log _ { 10 } \left( 0.707 \frac { \mathrm { Vout } } { \mathrm { Vin } } \right) } \end{array} $$
對於一階濾波器,濾波器的頻率響應曲線增加 20dB / decade 或 6dB /Octave,直到確定的截止頻率點,該截止頻率點始終低於最大增益值 -3dB。與之前的濾波器電路一樣,可以使用相同的公式找到較低的截止頻率( ƒc ):
$$ f _ { C } = \frac { 1 } { 2 \pi R C } \textrm {Hz} $$
輸出訊號的相應相位角或相移與無源 RC 濾波器的相位相位或相移相同,並超前輸入訊號的相位角或相移。它在截止頻率 ƒc 值處等於 +45o,如下所示:
$$ \text { Phase Shift } \phi = \tan ^ { - 1 } \left( \frac { 1 } { 2 \pi / R C } \right) $$
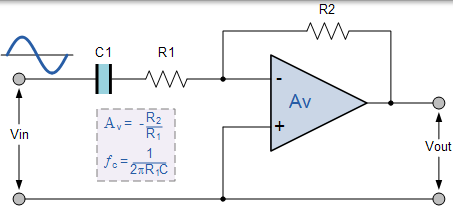
也可以使用反相運算放大器配置來製作簡單的一階有源高通濾波器,並且給出該電路設計的示例以及其對應的頻率響應曲線。假設電路增益為 40dB。
反相運算放大器電路
頻率響應曲線

有源高通濾波器示例 No1
一階有源高通濾波器的通帶增益為 2,截止頻率為 1kHz。如果輸入電容的值為 10nF,根據截止頻率來確定電阻和反饋網路中的增益電阻的值。另外,繪製濾波器的預期頻率響應。
截止轉角頻率為 1kHz,電容為 10nF,因此 R 的值為 :
$$ \mathrm { R } = \frac { 1 } { 2 \pi f _ { \mathrm { c } } \mathrm { C } } = \frac { 1 } { 2 \pi .1000 .10 \times 10 ^ { - 9 } } = 15.92 \mathrm { kS } $$
或選擇最接近的首選值 - 16kΩ。
因此,濾波器的通帶增益 AF 因此為2。
$$ \mathrm { A } _ { \mathrm { F } } = 1 + \frac { \mathrm { R } _ { 2 } } { \mathrm { R } _ { 1 } } , \quad \therefore 2 = 1 + \frac { \mathrm { R } _ { 2 } } { \mathrm { R } _ { 1 } } \quad \text { and } \quad \frac { \mathrm { R } _ { 2 } } { \mathrm { R } _ { 1 } } = 1 $$
電阻值 R2 除以電阻值 R1 的值為 1。然後,電阻器 R1 必須等於電阻器 R2,因為通帶增益 AF = 2。因此,我們可以為兩個電阻選擇合適的值,例如,每個電阻為 10kΩ,用於兩個反饋電阻。
因此,對於具有為 1kHz 的截止轉角頻率的高通濾波器,R 和 C 的值將分別是 10kΩ 和 10nF。產生兩個通帶增益的兩個反饋電阻的值如下: R1 = R2 =10kΩ。
頻率響應波特圖的資料可以通過將上面獲得的值在 100Hz 到 100kHz 的頻率範圍內代入電壓增益的等式來獲得:
$$ \text { Voltage Gain, } ( \mathrm { Av } ) = \frac { \text { Vout } } { \mathrm { Vin } } = \frac { \mathrm { A } _ { \mathrm { F } } \left( \frac { f } { f \mathrm { c } } \right) } { \sqrt { 1 + \left( \frac { f } { f \mathrm { c } } \right) ^ { 2 } } } $$
然後,這將為我們提供以下資料表。
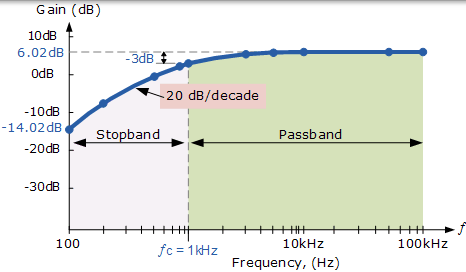
| 頻率 f(Hz) | 電壓增益 ( Vo / Vin ) | 增益(dB) 20log( Vo / Vin ) |
|---|---|---|
| 100 | 0.20 | -14.02 |
| 200 | 0.39 | -8.13 |
| 500 | 0.89 | -0.97 |
| 800 | 1.25 | 1.93 |
| 1000 | 1.41 | 3.01 |
| 3000 | 1.90 | 5.56 |
| 5000 | 1.96 | 5.85 |
| 10000 | 1.99 | 5.98 |
| 50000 | 2.00 | 6.02 |
| 100000 | 2.00 | 6.02 |
現在可以如下所示繪製上表中的頻率響應資料。在阻帶(從 100Hz 到 1kHz),增益以 20dB / decade 的速率增加。但是,在截止頻率ƒC = 1kHz 後的通帶,增益保持在恆定 6.02 分貝。通帶的頻率上限由我們前面討論過的運算放大器的開環頻寬決定。然後濾波器電路的波特圖將如下所示。
例子的頻率響應波特圖
應用有源高通濾波器是在音訊放大器,均衡器或揚聲器系統的高頻訊號引導到較小的高音揚聲器或以減少任何低頻噪聲或“隆隆聲”型別的失真。當在音訊應用中使用這樣的時,有源高通濾波器有時被稱為“高音增強”濾波器。
二階高通有源濾波器
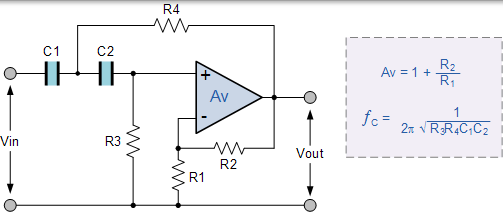
與無源濾波器一樣,只需在輸入路徑中使用額外的 RC 網路,即可將一階高通有源濾波器轉換為二階高通濾波器。二階高通濾波器的頻率響應與一階型別的頻率響應相同,只是阻帶衰減將是一階濾波器的兩倍 - 40dB /decade(12dB/Octave)。因此,二階有源高通濾波器所需的設計步驟是相同的。
二階有源高通濾波器電路
通過將第一和第二階濾波器級聯在一起,簡單地形成高階高通有源濾波器,例如3階,4階等。例如,通過級聯一階和二階濾波器形成三階高通濾波器,通過將兩個二階濾波器級聯在一起形成四階高通濾波器,依此類推。
然後,具有偶數序號的有源高通濾波器將僅包含二階濾波器,而奇數階數將從開頭的一階濾波器開始,如圖所示。
級聯有源高通濾波器
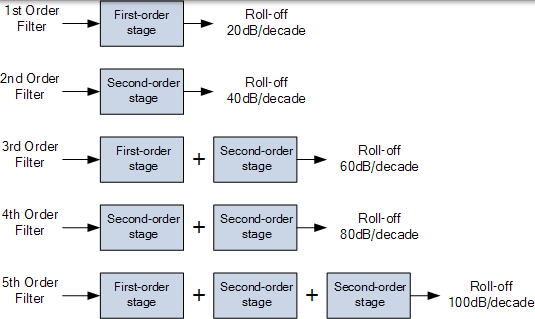
儘管對可以形成的濾波器的順序沒有限制,但是隨著濾波器的階數增加而其尺寸也增加。而且,其精度下降,即實際阻帶響應與理論阻帶響應之間的差異也增加。
如果頻率確定電阻器全部相等,R1 = R2 = R3 等,並且頻率確定電容器全部相等,C1 = C2 = C3 等,那麼任何濾波器階數的截止頻率將完全相同。然而,高階濾波器的總增益是固定的,因為所有頻率確定分量都相等。
在下一個關於濾波器的教程中,我們將看到有源帶通濾波器可以通過將高通和低通濾波器級聯在一起來構建。