電容和充電

電容器以電荷的形式將電能儲存在其板上

電容器由兩個平行的導電板（通常是金屬）組成，它們被稱為“電介質”的絕緣材料防止彼此接觸（分離）。當向這些板施加電壓時，電流以相對於電源電壓的正電荷向一個板充電，而另一個板以相等且相反的負電荷充電。

然後，電容器具有能夠儲存電子的電荷 Q （以庫侖為單位）的能力。當電容器完全充電時，其板之間存在電位差，pd 和板的面積越大和/或它們之間的距離越小（稱為分離），電容器可以容納的電荷就越大，它的電容就越大。

電容器在其板之間儲存該電荷（ Q）的能力與所施加的電壓 V 成比例，對於已知電容的電容器，以法拉為單位。請注意，電容 C 始終為正，從不為負。

施加的電壓越大，儲存在電容器極板上的電荷就越大。同樣，施加的電壓越小，電荷越小。因此，電容板上的實際電荷 Q 可以計算為：

對電容器充電

其中： Q （充電，以庫侖計）= C （電容，單位為法拉）x V （電壓，單位為伏特）

通過使用圖片有時更容易記住這種關係。這裡三個量的 Q，C 和 V 疊加成三角形，在頂部給電荷，底部有電容和電壓。這種安排代表電容器充電公式中每個數量的實際位置。

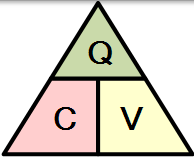
並且轉置上面的等式給出了以下相同等式的組合：

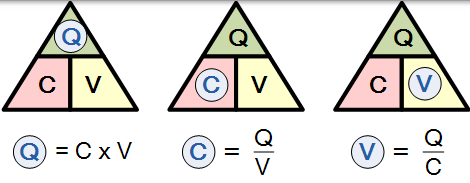
單位： Q 以庫侖為單位測量，V 以伏特為單位，C 以法拉為單位。

然後從上面我們可以定義電容的單位為庫侖/伏特，其也被稱為法拉，單位 F 。

由於電容代表電容器在其板上儲存電荷的能力（容量），我們可以將一個法拉定義為電容器的電容，其需要一個庫侖的電荷以在其板之間建立一伏的電位差。。因此，電容越大，對於相同電壓量，電容器上儲存的電荷量就越高。

電容器在其導電板上儲存電荷的能力使其具有電容值。電容也可以根據板的尺寸或面積，A 和板之間的介電材料的性質來確定。介電材料的量度由介電常數，（ ε）或介電常數給出。因此，表達電容器電容的另一種方法是：

電容器以空氣為電介質

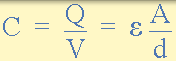
電容器以固體為電介質

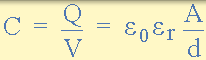
其中 A 是平板面積，m2 面積越大，電容器可以儲存的電荷越多。d 是兩個板之間的距離或間隔。這個距離越小，電極板儲存電荷的能力就越高，因為-Q 帶電電極板上的-ve 電荷對+ Q 帶電電極板的影響更大，導致更多的電子被+排斥。Q 充電板，從而增加整體充電量。

ε 0 （ε）是介電常數為空氣，其值是 8.84×10-12 F / m 和 ε R 是在兩個板之間所使用的電介質的介電常數。

平行板電容器

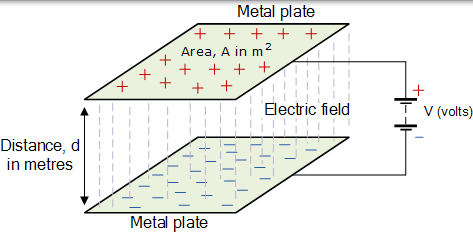
我們以前曾表示，平行板電容器的電容正比於表面積甲和反比於距離 d 的兩個板之間，這對於空氣的電介質如此。然而，通過在導電板之間插入介電常數大於空氣的介電常數，可以增加電容器的電容值。

各種常用介電材料的典型 ε 值為 ： 空氣= 1.0，紙= 2.5 - 3.5，玻璃= 3 - 10，雲母= 5 - 7 等。

與空氣相比，介電材料或絕緣體增加電容器電容的因素被稱為介電常數 （k）。 k 是所用介電介質的介電常數與自由空間介電常數之比，也稱為真空。

因此，所有電容值都與真空的介電常數有關。具有高介電常數的介電材料是比具有較低介電常數的介電材料更好的絕緣體。介電常數是無量綱的，因為它相對於自由空間。

電容示例 No1

平行板電容器由兩個板組成，總表面積為 100cm2。如果板間距為 0.2 釐米，電容器的微微法拉電容（pF）是多少，所用的電介質是空氣。

那麼電容的值是 44pF。

電容器的充電和放電

考慮以下電路。

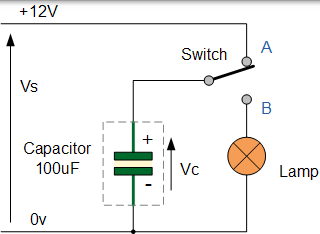
假定電容器完全放電並連線至所述電容器的開關剛被移動至位置甲。此時 100uF 電容器兩端的電壓為零，充電電流（i）開始向電容器充電，直到電路板上的電壓等於 12v 電源電壓。充電電流停止流動，電容器被稱為“完全充電”。然後，Vc = Vs = 12v。

一旦電容器在理論上“完全充電”，即使供電電壓已經斷開，它也將保持其電壓充電狀態，因為它們充當一種臨時儲存裝置。然而，雖然“理想”電容器可能也是如此，但由於內部洩漏電流流過電介質，實際電容器將在很長一段時間內緩慢放電。

這是一個需要記住的重點，因為即使電源電壓“關閉”，連線在高壓電源上的大值電容仍然可以保持大量電量。

如果此時開關斷開，電容器將無限期地保持其電荷，但由於內部漏電流流過其電介質，電容器將非常緩慢地開始自身放電，因為電子通過電介質。電容器放電至其電源電壓的 37％所需的時間稱為時間常數 。

如果開關現在從位置 A 移動到位置 B，則完全充電的電容器將開始通過現在連線在其上的燈放電，照亮燈直到電容器完全放電，因為燈的元件具有電阻值。

燈的亮度和照明持續時間最終取決於電容器的電容值和燈的電阻（ t = R * C）。電容器的值越大，燈的發光越亮越長，因為它可以儲存更多的電荷。

電容器充電示例 No2

計算上述電容器電路中的電荷。

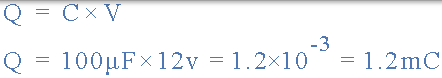
那麼電容器上的電荷是 1.2 毫庫侖。

電流通過電容器

由於兩個極板之間的介電材料的絕緣特性，電流實際上不能流過電容器，因為它是電阻器或電感器。然而，兩個板的充電和放電產生電流流動的效果。

流過電容器的電流與板上的電荷直接相關，因為電流是電荷相對於時間的流速。由於電容器在其極板之間儲存電荷（ Q）的能力與施加的電壓（ V） 成比例，因此電流和施加到電容器極板的電壓之間的關係變為：

電流 - 電壓（IV）關係

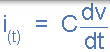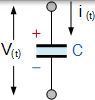隨著板上的電壓隨時間增加（或減小），流過電容的電流從其板沉積（或移除）電荷，其中電荷量與施加的電壓成比例。然後，施加到電容的電流和電壓都是時間函式，並由符號 i(t) 和 v(t)表示。

但是，根據上式，我們還可以看到，如果電壓保持不變，電荷將變為常數，因此電流將為零！ 換句話說，電壓沒有變化，沒有電荷移動和沒有電流。這就是當連線到穩態 DC 電壓時電容器似乎“阻塞”電流的原因。

法拉

我們現在知道電容器儲存電荷的能力給它的電容值 C，其單位為法拉，F 。但法拉本身就是一個非常大的單位，因此使用它是不切實際的，因此使用標準法拉單位的子多數或分數。

為了瞭解 Farad 究竟有多大，需要製作一個僅為 1 法拉的電容器所需的板的表面積，在真空中操作合理的板間距僅為 1mm。如果我們重新排列上面的電容等式，我們將得到一個板面積：

A = Cd÷8.85pF / m =（1×0.001）÷8.85×10-12 = 112,994,350 m2

或 1.13 億米 2 這將是相當於 10 公里以上×10 千米（超過 6 英里）的正方形的板。那是巨大的。

具有一法拉或更大值的電容器傾向於具有固體電介質並且“一法拉”是如此大的單位使用，字首用於電子公式中，其中電容器值以微法（ μF）給出，納米-Farads（ nF）和 pico-Farads（ pF）。例如：

法拉的子單位

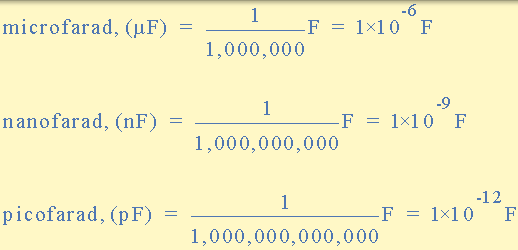
將以下電容值從 a） 22nF 轉換為 μF，b） 0.2μF 轉換為 nF，c） 550pF 轉換為 μF。

a2 2nF =0.022μF

b0 .2μF= 200nF

c5 50pF =0.00055μF

雖然一個法拉是一個很大的價值，但電容現在通常可用，電容值為幾百法拉，其名稱反映了“超級電容器”或“超級電容器”的名稱。

這些電容器是電化學能量儲存裝置，其利用其碳電介質的高表面積來傳遞比傳統電容器高得多的能量密度，並且電容與碳的表面積成比例，碳越厚，電容越大。

低電壓（約 3.5V 至 5.5V）超級電容器由於其高電容值而能夠儲存大量電荷，因為儲存在電容器中的能量等於 1/2（C×V2）。

低壓超級電容器通常用於行動式手持裝置中，以取代大型，昂貴且重型鋰電池，因為它們具有類似電池的儲存和放電特性，使其非常適合用作替代電源或用於儲存器備份。手持裝置中使用的超級電容器通常使用安裝在裝置上的太陽能電池充電。

正在開發用於混合動力電動汽車和替代能源應用的超級電容器，以取代大型傳統電池以及車輛音訊和視訊系統中的 DC 平滑應用。超級電容器可以快速充電，並具有非常高的儲能密度，使其成為電動汽車應用的理想選擇。

電容器中的能量

當電容器從連線到其的電源充電時，建立靜電場，其將能量儲存在電容器中。儲存在該靜電場中的焦耳能量等於電壓供應用於維持電容器極板上的電荷的能量，並由下式給出：

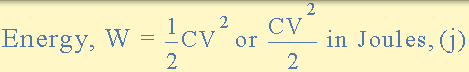
所以儲存在上述 100uF 電容器電路中的能量計算如下：

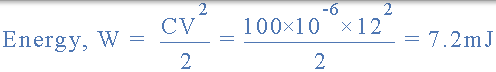
在我們關於電容器的部分的下一個教程中，我們看一下電容器顏色程式碼，並看到電容器的電容和電壓值標記在其主體上的不同方式。