正弦波形
當電流流過導線或導體時,在導線周圍產生圓形磁場,其強度與電流值有關。
如果該單線導體在靜止磁場內移動或旋轉,則由於導體通過磁通量的移動而在導體內感應出 EMF (電動勢)。
由此我們可以看出,電力和磁力之間存在著一種關係,正如邁克爾·法拉第發現“電磁感應”的影響一樣,電機和發電機用來為我們的主電源產生正弦波形是這個基本原理。
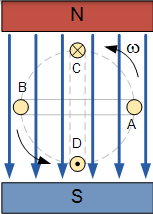
在電磁感應教程中,我們說當單線導體穿過永久磁場從而切斷其磁通線時,會在其中感應出 EMF。
但是,如果導體在點 A 和 B 的情況下與磁場平行移動,則沒有切割磁通線並且沒有 EMF 被感應到導體中,但是如果導體與磁場成直角移動,如在在點 C 和 D 的情況下,切割最大磁通量,產生最大量的感應 EMF。
另外,作為導體切割磁場的點之間的不同角度甲和 C ,0 和 90o 感應 EMF 的量將某處該零和最大值之間。然後,導體內感應的電動勢的量取決於導體與磁通量之間的角度以及磁場的強度。
交流發電機利用法拉第的電磁感應原理將機械能(如旋轉)轉換為電能,即正弦波形。簡單的發電機由一對永久磁鐵組成,在北極和南極之間產生固定的磁場。在該磁場內部是單個矩形線圈,其可以圍繞固定軸旋轉,允許其以各種角度切割磁通量,如下所示。
基本單線圈交流發電機

當線圈圍繞垂直於磁場的中心軸逆時針旋轉時,線環在環路旋轉時以不同的角度切割在北極和南極之間建立的磁力線。在任何時刻,環路中感應的 EMF 的量與線環的旋轉角度成比例。
當該線圈旋轉時,線中的電子圍繞環在一個方向上流動。現在,當線圈旋轉超過 180° 點並沿相反方向的磁力線移動時,線圈中的電子改變並沿相反方向流動。然後電子運動的方向決定了感應電壓的極性。
因此我們可以看到,當環路或線圈物理旋轉一整圈或 360° 時,產生一個完整的正弦波形,波形的每一圈產生一個波形週期。當線圈在磁場內旋轉時,通過碳刷和滑環對線圈進行電連線,碳刷和滑環用於傳遞線圈中感應的電流。
引入切割磁力線的線圈中的 EMF 量由以下三個因素確定。
- 速度 - 線圈在磁場內旋轉的速度。
- 強度 - 磁場的強度。
- 長度 - 通過磁場的線圈或導體的長度。
我們知道電源的頻率是一個週期在一秒鐘內出現的次數,並且該頻率以赫茲為單位測量。如上所示,通過包括北極和南極的磁場,線圈的每次完整旋轉產生一個感應電動勢迴圈,如果線圈以恆定速度旋轉,則每秒產生恆定數量的迴圈,給出恆定的頻率。因此,通過增加線圈的旋轉速度,頻率也將增加。因此,頻率與旋轉速度成比例,( ƒ ∝ N)其中 N = rpm。
此外,我們上面的簡單單線圈發電機只有兩個極,一個是北極,另一個是南極,這是一對極。如果我們在發電機上面新增更多的磁極,使其現在總共有四個極,兩個北極和兩個南極,那麼對於線圈的每次旋轉,將產生兩個相同轉速的迴圈。因此,頻率與發電機的磁極對數成比例( ƒ ∝ P),其中 P = 極對數。
然後根據這兩個事實,我們可以說 AC 發電機的頻率輸出是:
$$ f = \frac {NP}{60} \mathrm{Hz} $$
其中: Ν 是 rpm 轉速, P 是極對數,60 將結果轉換為 1/秒。
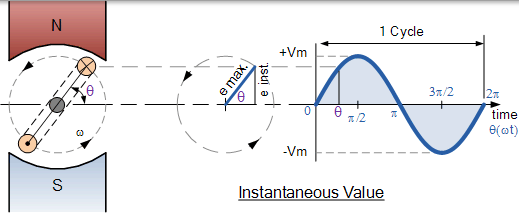
瞬時電壓
在任何時刻線上圈中感應的 EMF 取決於線圈切割磁極之間的磁通線的速率或速度,這取決於發電裝置的旋轉角度 θ。由於 AC 波形不斷改變其值或幅度,因此任何時刻的波形將具有與其下一個時刻不同的值。
例如,1ms 處的值將與 1.2ms 處的值不同,依此類推。這些值通常稱為瞬時值,或 Vi。 然後,波形的瞬時值及其方向將根據線圈在磁場內的位置而變化,如下所示。
磁場內線圈的位移

正弦波形的瞬時值由瞬時值=最大值 x sinθ 給出,
$$ V _ { i } = V _ { \max } \times \sin \theta $$
其中,Vmax 是線圈中感應的最大電壓, θ=ωt,是線圈相對於時間的旋轉角度。
如果我們知道波形的最大值或峰值,通過使用上面的公式,可以計算沿波形的各個點的瞬時值。通過將這些值繪製到方格紙上,可以構造正弦波形。
為了簡單起見,我們將在每 45o 繪製正弦波形的瞬時值,這樣每個週期內我們有 8 個點來繪製。同樣,為了保持簡單,我們將假設最大電壓,VMAX 值為 100V。以較短的間隔繪製瞬時值,例如每 30o (12 個 點)或 10o (36 個點),將導致更準確的正弦波形構造。
正弦波形構造
| 線圈角度(θ) | 0 | 45 | 90 | 135 | 180 | 225 | 270 | 315 | 360 |
|---|---|---|---|---|---|---|---|---|---|
| e =Vmax * sinθ | 0 | 70.71 | 100 | 70.71 | 0 | -70.71 | -100 | -70.71 | -0 |
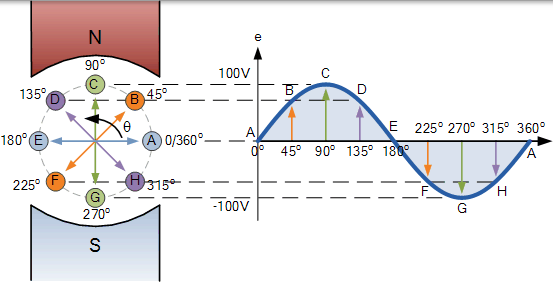
正弦波形的點由 0o到 360o 之間不同旋轉位置向代表角度 θ 的座標軸來投影得到的,當線環或線圈旋轉一個整圈,或到達 360o 後,產生一個完整的波形。
從正弦波形圖可以看出,當 θ 等於 0°、180° 或 360° 時,生成的 EMF 為零,因為線圈切割最小量的磁通量。但是,當 θ 等於 90o 和 270o 時,所產生的 EMF 是處於其最大值,因為最大的磁通量被切割。
因此正弦波形在 90o 具有正峰值,並在 270o 時有負峰值。位置 B,D,F 和 H 產生對應於下式的 EMF 值: e =Vmax * sinθ。
然後,由我們的簡單單線圈發電機產生的波形形狀通常被稱為正弦波,因為它的形狀是正弦波。這種型別的波形稱為正弦波,因為它基於數學中使用的三角正弦函式,( x(t)=Amax * sinθ)。
當處理時域中的正弦波,尤其是當前相關的正弦波時,沿波形的水平軸使用的測量單位可以是時間,度或弧度。在電氣工程中,更常見的是使用弧度作為沿水平軸而不是角度的角度測量。例如, ω = 100rad/s,或 500rad/s。
弧度
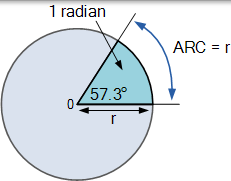
弧度(RAD)在數學上被定義為一個圓的一部分,其中它的弧長等於同一個圓的半徑。由於圓的周長等於 2π x 半徑,360o 的圓的必須有 2π 個弧度。
換句話說,弧度是角度測量的單位,並且一個弧度的長度(r)的6.284(2 *π)倍將圍繞圓一週。因此,一個弧度等於 360o /2π= 57.3o 。在電氣工程中,弧度的使用非常普遍,因此記住以下公式非常重要。
Radian 的定義
$$ \begin{array} { c } { 2 \pi \mathrm { rads } = 360 ^ { \circ } } \ { \therefore 1 \mathrm { rad } = 57.3 ^ { \circ } } \end{array} $$
使用弧度作為正弦波形的測量單位將為 360o 的 一個完整週期提供 2π 個弧度。然後,半個正弦波形必須等於 1π 弧度。然後我們知道 π 等於 3.142,因此正弦波形的度和弧度之間的關係如下,
度和弧度之間的關係
$$ \begin{array} { l } { \text { Radians } = \left( \frac { \pi } { 180 ^ { \circ } } \right) \times \text { degrees } } \\ { \text { Degrees } = \left( \frac { 180 ^ { \circ } } { \pi } \right) \times \text { radians } } \end{array} $$
將這兩個方程應用於沿波形的各個點,我們將得到,
$$ 30 ^ { \circ } \rightarrow \text { Radians } = \frac { \pi } { 180 ^ { \circ } } \left( 30 ^ { \circ } \right) = \frac { \pi } { 6 } \mathrm { rad } $$
$$ 90 ^ { \circ } \rightarrow \text { Radians } = \frac { \pi } { 180 ^ { \circ } } \left( 90 ^ { \circ } \right) = \frac { \pi } { 2 } \mathrm { rad } $$
$$ \frac { 5 \pi } { 4 } \mathrm { rad } \rightarrow \text { Degrees } = \frac { 180 ^ { \circ } } { \pi } \left( \frac { 5 \pi } { 4 } \right) = 225 ^ { \circ } $$
$$ \frac { 3 \pi } { 2 } \mathrm { rad } \rightarrow \text { Degrees } = \frac { 180 ^ { \circ } } { \pi } \left( \frac { 3 \pi } { 2 } \right) = 270 ^ { \circ } $$
對於正弦分析中使用的更常見的等效關係,度和弧度之間的轉換在下表中給出。
度和弧度之間的關係
| 角度 | 弧度 | 角度 | 弧度 | 角度 | 弧度 |
|---|---|---|---|---|---|
| 0o | 0 | 135o | 3π 4 | 270o | 3π 2 |
| 30o | π 6 | 150o | 5π 6 | 300o | 5π 3 |
| 45o | π 4 | 180o | π | 315o | 7π 4 |
| 60o | π 3 | 210o | 7π 6 | 330o | 11π 6 |
| 90o | π 2 | 225o | 5π 4 | 360o | 2π |
| 120o | 2π 3 | 240o | 4π 3 |
發電機圍繞其中心軸旋轉的速度決定了正弦波形的頻率。由於波形的頻率 ƒ 單位為 Hz 或週期每秒,波形還具有角頻率 ω ,以弧度/秒為單位。然後給出正弦波形的角速度,
正弦波形的角速度
$$ \omega = 2 \pi f ( \text { rad } / \text { sec } ) $$
在國內,主電源的角速度或頻率如下: $$ \omega = 2 \pi f = 2 \pi .50 = 314.2 \mathrm { rad } / \mathrm { s } $$
在美國,由於其主電源頻率為 60Hz,因此我們可以得到 - 377 rad/s
因此,我們現在知道,在其中發電機繞其中心軸旋轉速度決定了正弦波形的頻率和其也可以稱為其角速度 ω。但是我們現在也應該知道完成一整圈所需的時間等於正弦波形的週期時間( T)。
頻率成反比於週期, ƒ= 1 / T, 因此,我們我們可以通過週期來計算出角頻率,
$$ \omega = \frac { 2 \pi } { \mathrm { T } } ( \mathrm { rad } / \mathrm { sec } ) $$
上述等式表明,正弦波的週期時間越小,波形的角速度就越大。同樣在上面對於頻率量的等式中,頻率越高,角速度越高。
正弦波形示例 No1
有一正弦波形 Vm = 169.8 sin(377t) V。計算波形的 RMS 電壓,其頻率,及在 6 毫秒(6ms)的時間上電壓的瞬時值(Vi)。
我們從上面知道,正弦波形的一般表示式是: $$ \mathrm { V } _ { ( \mathrm { t } ) } = \mathrm { V } _ { \mathrm { m } } \sin ( \mathrm { \omega t } ) $$
然後將其與我們給定的高於 Vm = 169.8 sin(377t) 的正弦波形的表示式進行比較,將得到波形的峰值電壓值 169.8 伏。
波形 RMS 電壓計算如下:
$$ { \mathrm { V } _ { ( \mathrm { ms } ) } = 0.707 \times \mathrm { maximum } \text { peak value } } \\ { \mathrm { V } _ { ( \mathrm { ms } ) } = 0.707 \times 169.8 = 120 \mathrm { volts } } $$
角速度( ω)為 377 rad/s。然後 2πƒ= 377。因此波形的頻率計算如下:
$$ \text { Frequency } ( f ) = \frac { 377 } { 2 \pi } = 60 \mathrm { Hz } $$
6ms 時間後的瞬時電壓 Vi 值如下:
$$ \mathrm { V } _ { ( \mathrm { i } ) } = \mathrm { V } _ { \mathrm { m } } \sin \left( \omega \mathrm { t } \right) \\ { \mathrm { V } _ { ( \mathrm { i } ) } = 169.8 \sin ( 377 \times 0.006 ) } \\ \mathrm { V } _ { ( \mathrm { i } ) } = 169.8 \sin ( 2.262 \mathrm { rads } ) \\ 2.262 \mathrm { rads } \times 57.3 ^ { \circ } = 129.6 ^ { \circ } \\ V _ { ( 1 ) } = 169.8 \sin \left( 129.6 ^ { \circ } \right) = 169.8 \times 0.771 \\ \therefore V _ { ( 1 ) } = 130.8 \text { volts peak } $$
注意,時間 t = 6ms 處的角速度以弧度( rads)給出。如果願意,我們可以將其轉換為等效角度,並使用該值代替計算瞬時電壓值。因此,瞬時電壓值的角度為:
$$ \begin{array} { c } { \text { Degrees } = \left( \frac { 180 ^ { \circ } } { \pi } \right) \times \text { radians } } \\ { \therefore \frac { 180 ^ { \circ } } { \pi } \times 2.262 = 57.3 ^ { \circ } \times 2.262 = 129.6 ^ { \circ } } \end{array} $$
正弦波形
然後,用於分析和計算正弦波形的各種值的通用格式如下:
正弦波形
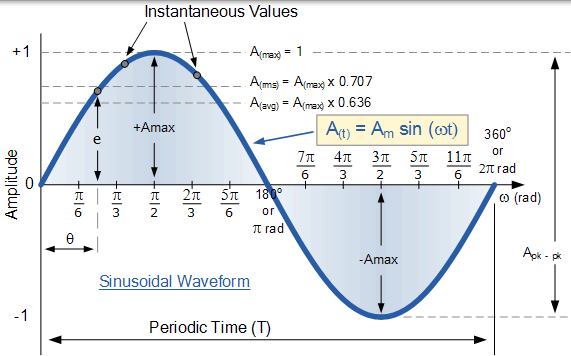
在下一節關於相位差的教程中,我們將研究兩個具有相同頻率但在不同時間間隔通過水平零軸的正弦波形之間的關係。