串聯 RLC 電路分析
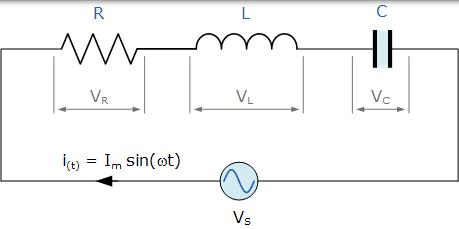
RLC 系列電路由交流電源串聯的電阻,電容和電感組成
到目前為止,我們已經看到三個基本的無源元件: 電阻,電感和電容*在連線到正弦交流電源時彼此具有非常不同的相位關係。
在純歐姆電阻器中,電壓波形與電流“同相”。在純電感電壓波形“導致”目前由 90o,給我們的表達:ELI。在純電容中,電壓波形“滯後”電流 90o,給出了表示式:ICE。
這個相位差,Φ 取決於所使用的元件的無功值,並且希望現在我們知道電抗,( X)如果電路元件是電阻則為零,如果電路元件是電感元件則為正,如果電容元件是電容元件則為負給出它們產生的阻抗:
元素阻抗
| 電路元件 | 阻力,(R) | 電抗,(X) | 阻抗,(Z) |
| 電阻 | [R | 0 | 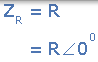 |
| 感應器 | 0 | ωL | 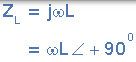 |
| 電容器 | 0 | 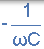 |
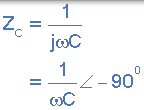 |
我們可以將所有三個組合在一起成為一串聯 RLC 電路,而不是分別分析每個無源元件。一串聯 RLC 電路的分析與我們之前看到的雙串聯 RL 和 RC 電路的分析相同,除了這次我們需要考慮 XL 和 XC 的幅度來找到整個電路電抗。串聯 RLC 電路被歸類為二階電路,因為它們包含兩個儲能元件,即電感大號和電容 C ^ 。考慮下面的 RLC 電路。
串聯 RLC 電路

上面的串聯 RLC 電路具有單個環路,流過環路的瞬時電流對於每個電路元件是相同的。由於電感和電容電抗的 XL 和 XC 是電源頻率的函式,因此串聯 RLC 電路的正弦響應將隨頻率 f 而變化。然後,R,L 和 C 元件的每個電路元件上的各個電壓降將彼此“異相”,如下所定義:
- i(t) = Imax sin(ωt)
- 純電阻器 VR 上 的瞬時電壓與電流“同相”
- 純電感器上的瞬時電壓 VL “導通”電流 90o
- 純電容器上的瞬時電壓 VC “滯後”電流 90o
- 因此,VL 和 VC ^ 是 180o “外的相位”,並在彼此相對。
對於上面的 RLC 系列電路,可以顯示為:

串聯 RLC 電路中所有三個元件的源極電壓幅度由三個獨立的分量電壓 VR,VL 和 VC 組成,其中所有三個元件共用電流。因此,向量圖將具有電流向量作為其參考,其中三個電壓向量相對於該參考繪製,如下所示。
各個電壓向量

這意味著我們不能簡單地將 VR,VL 和 VC 加在一起以找到所有三個分量上的電源電壓 VS,因為所有三個電壓向量指向關於電流向量的不同方向。因此,我們必須找到電源電壓 VS 作為三個分量電壓的向量和,它們組合在一起。
環路和節點電路的基爾霍夫電壓定律(KVL)表明,在任何閉環周圍,環路周圍的電壓降之和等於 EMF 的總和。然後將這個定律應用於這三個電壓將給出我們的源電壓幅度,VS as。
串聯 RLC 電路的瞬時電壓
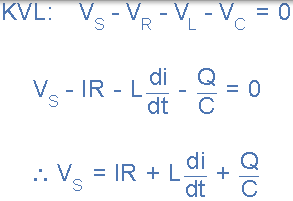
通過將上述三個單獨的相量組合在一起並向量地新增這些電壓來產生串聯 RLC 電路的相量圖。由於流過電路的電流對於所有三個電路元件是共同的,因此我們可以將其用作參考向量,其中三個電壓向量以相應的角度相對於此繪製。
將得到的向量 VS 通過新增在一起的兩個向量,所獲得的 VL 和 VC ^,然後加入此總和到其餘向量 VR。在 VS 和 i 之間獲得的最終角度將是電路相位角,如下所示。
串聯 RLC 電路的相量圖
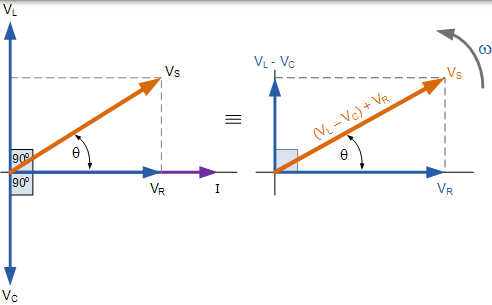
從右上方的相量圖可以看出,電壓向量產生一個矩形三角形,包括斜邊 VS,水平軸 VR 和垂直軸 VL - VC 希望你會注意到,這形成了我們的老最喜歡的電壓三角因此,我們可以利用這個電壓三角形畢達哥拉斯定理在數學上獲得的價值 VS,如圖所示。
串聯 RLC 電路的電壓三角形
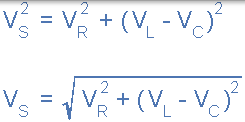
請注意,使用上述公式時,最終的無功電壓必須始終為正值,即最小電壓必須始終從最大電壓中取出,我們不能將負電壓加到 VR 上, 因此它是正確的有 VL - VC 或 VC - VL。最大的最小值,否則計算 VS 將是不正確的。
我們從上面知道,電流在一串聯 RLC 電路的所有元件中具有相同的幅度和相位。然後,也可以根據流過的電流和每個元件兩端的電壓數學地描述每個元件兩端的電壓。
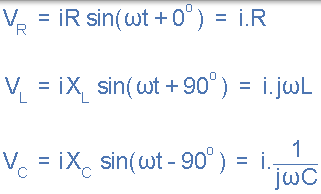
通過將這些值代入上面的畢達哥拉斯方程中的電壓三角形將給我們:
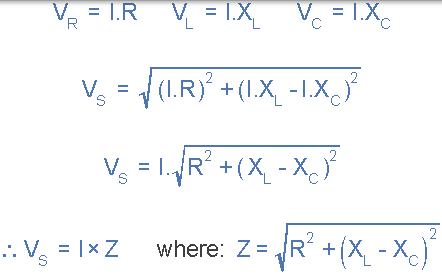
因此我們可以看到源電壓的幅度與流過電路的電流的幅度成比例。該比例常數稱為電路的阻抗,其最終取決於電阻以及電感和電容電抗。
然後,在上述的串聯 RLC 電路,可以看出的是,反對電流流動是由三個部分組成,XL,XC 和 - [R 與電抗,XT 任何 RLC 串聯電路被定義為: XT = XL - XC 或 XT = XC - X.L 哪個更大。因此,電路的總阻抗被認為是驅動電流通過它所需的電壓源。
串聯 RLC 電路的阻抗
由於三個向量電壓彼此異相,因此 XL,XC 和 R 也必須彼此“異相”,R,XL 和 XC 之間的關係是向量和這三個組成部分。這將使我們的 RLC 電路總阻抗, Z 。這些電路阻抗可以用阻抗三角形繪製和表示 **** 如下所示。
串聯 RLC 電路的阻抗三角形
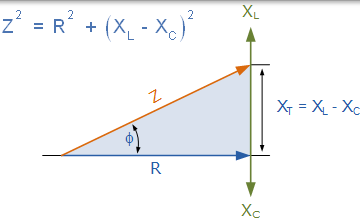
串聯 RLC 電路的阻抗 Z 取決於角頻率 ω,XL 和 XC 也是如此。 如果容抗大於感抗,XC > XL 則整個電路電抗是電容性的,給出一個超前相角。
同樣,如果感抗小於容抗,XL > XC 則整個電路電抗是電感性的,從而使串聯電路具有滯後相位角。如果這兩個電抗的是相同的,XL = XC 然後發生這種情況被稱為共振頻率,併產生效果的角頻率共振,我們將看更詳細的另一個教程。
那麼電流的大小取決於施加到串聯 RLC 電路的頻率。當阻抗 Z 處於其最大值時,電流是最小值,同樣,當 Z 處於其最小值時,電流處於最大值。所以上面的阻抗方程可以重寫為:
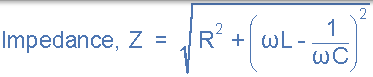
源電壓 VS 和電流 i 之間的相位角 θ 與阻抗三角形中 Z 和 R 之間的角度相同。取決於源電壓是否超前或滯後電路電流,該相位角可以是正值或負值,並且可以從阻抗三角形的歐姆值數學計算為:
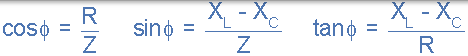
串聯 RLC 電路例項 No1
包含 12Ω 電阻,0.15H 電感和 100uF 電容的串聯 RLC 電路串聯連線在 100V,50Hz 電源上。計算總電路阻抗,電路電流,功率因數和繪製電壓相量圖。
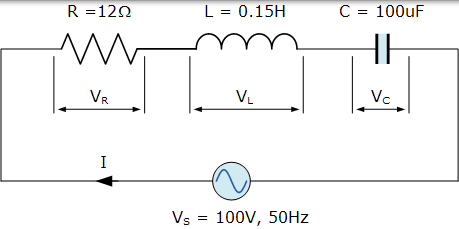
感抗,XL。

容抗,XC。
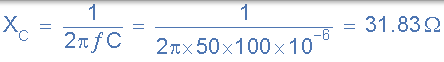
電路阻抗,Z。
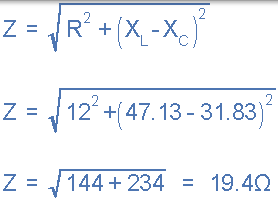
電路電流 I 。

在串聯 RLC 電路,電壓 VR,VL,VC。
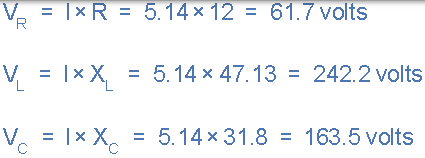
電路功率因數和相角 θ。
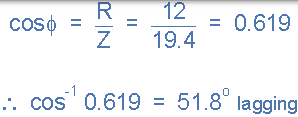
相量圖。
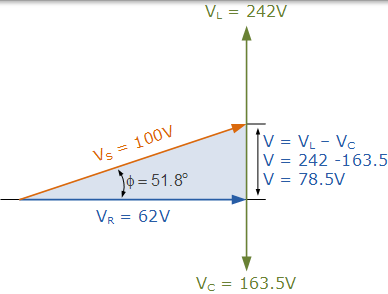
由於相位角 θ 作為 51.8 正值計算o 電路的總電抗必須是電感性的。由於我們已經將電流向量作為我們在串聯 RLC 電路中的參考向量,然後電流“滯後”源電壓 51.8o 所以我們可以說相位角是滯後的,這由我們的助記符表示式 ELI 證實。
串聯 RLC 電路概述
在包含電阻器,電感器和電容器的串聯 RLC 電路中,源電壓 VS 是由三個分量 VR,VL 和 VC 組成的相量和,其中三個分量電流共用。由於電流對於所有三個元件是共同的,因此在構造電壓三角形時將其用作水平參考。
電路的阻抗是與電流的完全相反。對於串聯 RLC 電路,可以通過將電壓三角形的每一側除以其電流 I 來繪製阻抗三角形。到在電阻元件上的電壓降等於 I * R,在這兩個反應性元件上的電壓是 I * X = I * XL I * X -C 而源極電壓等於餘* Z。VS 和 I 之間的角度將是相位角, θ。
當使用包含多個電阻的串聯 RLC 電路時,電容或電感要麼純淨,要麼不純,它們可以全部加在一起形成單個元件。例如,所有電阻加在一起,RT =(R1 + R2 + R3) …等或所有電感的 LT =(L1 + L2 + L3) ……這樣,包含許多元件的電路可以很容易地減少到單個阻抗。
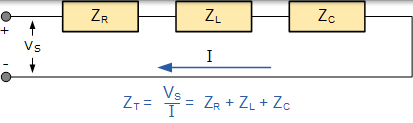
在下一個關於並聯 RLC 電路的教程中,我們將看一下當並聯電路配置時,在並聯電路配置中連線在一起的三個元件的電壓 - 電流關係以及相應的相量圖表示。我們還將首次介紹入場的概念。