RMS 電壓教程

正弦波形的 RMS 或有效值給出了等效直流電源的相同加熱效果

在我們關於 AC 波形的 教程中，我們簡要介紹了正弦波形的 RMS 電壓值，並說該 RMS 值與等效直流功率具有相同的加熱效果，在本教程中，我們將通過尋找更多的理論來擴充套件這一理論。在 RMS 電壓和電流更詳細。

術語 RMS 代表 Root-Mean-Squared。大多數書籍將此定義為“產生與等效直流電源相同的加熱效果的交流電量”，或者沿著這些線路類似的東西，但 RMS 值不僅僅是這個。RMS 值是瞬時值的平方函式的平均值（平均值）的平方根。用於定義 RMS 值的符號是 VRMS 或 IRMS。

術語 RMS，僅指時變正弦電壓，電流或複雜波形是波形隨時間變化的幅度，並且不用於直流電路分析或計算，其幅度始終是恆定的。當用於比較交流正弦波形的等效 RMS 電壓值時，RMS 值被稱為“有效值”，通常表示為： Veff 或 Ieff。

換句話說，有效值是一個等效的直流值，它可以告訴你在產生相同功率的能力方面，時變正弦波形等於多少伏特或安培的直流電壓。

例如，英國的國內主電源是 240Vac。假設該值表示“240 伏特 rms”的有效值。這意味著來自英國家庭的牆壁插座的正弦均方根電壓能夠產生與 240 伏穩定直流電壓相同的平均正電壓，如下所示。

RMS 電壓等效

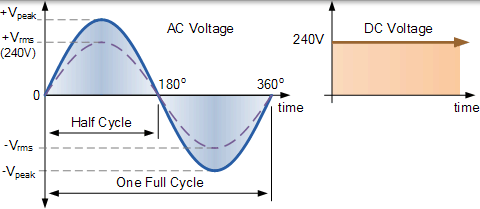
那麼我們如何計算正弦波形的 RMS 電壓。正弦波或複雜波形的 RMS 電壓可以通過兩種基本方法確定。

• 圖形方法 - 通過在波形上繪製多箇中點，可用於查詢任何非正弦時變波形的 RMS 值。
• 分析方法 - 是使用微積分找出任何週期性電壓或電流的有效或 RMS 值的數學過程。

RMS 電壓圖形方法

雖然對於 AC 波形的兩半計算方法是相同的，但是對於該示例，我們將僅考慮正半週期。通過沿波形採用等間隔瞬時值，可以以合理的精度找到波形的有效值或均方根值。

波形的正半部分為任意數量的 n 等分或中間座標，沿波形繪製的中間座標越多，最終結果就越準確。因此各中縱座標的寬度將 Ño 度和各中間縱座標的高度將等於波形的在沿著波形的 x 軸即時間的瞬時值。

圖形方法

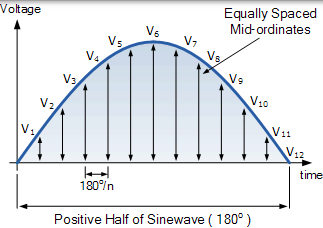
波形的每個中間座標值（在這種情況下為電壓波形）乘以其自身（平方）並新增到下一個。該方法為我們提供了 RMS 電壓表示式的“平方”或平方部分。接下來，這個平方值除以用於給出 RMS 電壓表示式的平均部分的中間數字，在上面的簡單示例中，使用的中間數字是十二（12）。最後，發現先前結果的平方根給出了 RMS 電壓的根部分。

然後，我們可以定義用於描述的 RMS 電壓（V 術語RMS）為“平方根的的平均值的的方形電壓波形的中間縱座標”，這被給定為：

對於上面的簡單示例，RMS 電壓計算如下：

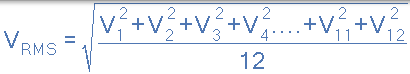
因此，假設交流電壓具有 20 伏的峰值電壓（ Vpk），並且通過取 10 箇中間值，發現在一個半週期內變化如下：

因此，RMS 電壓計算如下：

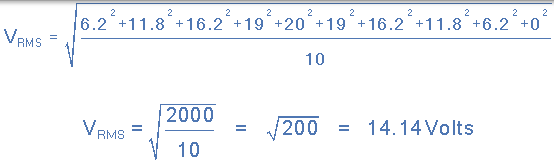
然後使用圖形方法的 RMS 電壓值為： 14.14 伏特。

RMS 電壓分析方法

上面的圖形方法是找到本質上不對稱或正弦的交流波形的有效或 RMS 電壓（或電流）的非常好的方法。換句話說，波形形狀類似於複雜波形。然而，當處理純正弦波形時，我們可以通過使用分析或數學方法找到 RMS 值，使我們自己的生活更容易一些。

週期性正弦電壓是恆定的，並且可以被定義為 V（t）的 = Vmax * COS（ωT） 用一段 Ť 。然後，我們可以計算出根均方的正弦電壓（V 的均方根（RMS）值(t)） 為：

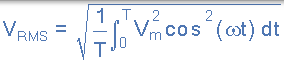
通過從 0 到 360o 或 T 的限制進行整合，期間給出：

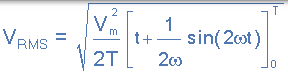
其中： Vm 是波形的峰值或最大值。進一步除以 ω=2π/ T，上面的複數方程也最終減小：

RMS 電壓方程

然後 RMS 電壓（ VRMS 正弦波形的）是通過由峰值電壓值乘以確定 0.7071，這是相同的一個由兩個（平方根除以 1 /√ 2 ）。RMS 電壓（也可稱為有效值）取決於波形的大小，而不是波形頻率或相位角的函式。

從上面的圖形示例中，波形的峰值電壓（ Vpk）給出為 20 伏特。通過使用剛定義的分析方法，我們可以將 RMS 電壓計算為：

VRMS = Vpk * 0.7071 = 20×0.7071 = 14.14V

請注意，此值為 14.14 伏特的值與上一個圖形方法的值相同。然後我們可以使用中間座標的圖形方法或計算的分析方法來找到正弦波形的 RMS 電壓或電流值。

請注意，將峰值或最大值乘以常數 0.7071，僅適用於正弦波形。對於非正弦波形，必須使用圖形方法。

但是，除了使用正弦曲線的峰值或最大值之外，我們還可以使用峰峰值（VPP）值或平均值（VAVG）來找到正弦曲線等效均方根值，如下所示：

正弦 RMS 值

RMS 電壓彙總

然後總結一下。在處理交流電壓（或電流）時，我們面臨著如何表示電壓或訊號幅度的問題。一種簡單的方法是使用波形的峰值。另一種常用方法是使用有效值，該有效值也通過其更均勻的均方根表示式或簡稱為 RMS 值而得知。

根均方，正弦曲線的 RMS 值與所有瞬時值的平均值不同。電壓的 RMS 值與電壓的最大值的比率與電流的 RMS 值與電流的最大值的比率相同。

大多數萬用表，無論是電壓表還是電流表，都可以測量 RMS 值，假設是純正弦波形。為了找到非正弦波形的 RMS 值，需要“真有效值萬用表”。

正弦波形的 RMS 值提供與相同值的 DC 電流相同的加熱效果。也就是說，如果直流電流 I 穿過的電阻 - [R 歐姆，由電阻器作為熱消耗的 DC 電源將因此 I2 - [R 瓦。然後，如果交流電流 i = Imax *sinθ 流過相同的電阻，則轉換成熱量的交流功率將為： I2rms * R 瓦。

然後，當處理交流電壓和電流時，除非另有說明，否則應將它們視為 RMS 值。因此，10 安培的交流電流將具有與 10 安培的直流電流和 14.14 安培的最大值相同的加熱效果。

現在已經確定了交流電壓（或電流）波形的 RMS 值，在下一個教程中，我們將研究計算交流電壓的平均值，VAVG，最後比較兩者。