功率三角和功率因數

構成 AC 電路中消耗的電功率的三個電路元件可以由直角三角形的三個邊來表示，通常稱為功率三角形

我們在關於電源的教程中看到，包含電阻和電容或電阻和電感或兩者的交流電路也包含有功功率和無功功率。因此，為了讓我們計算消耗的總功率，我們需要知道電壓和電流的正弦波形之間的相位差。

在交流電路中，電壓和電流波形是正弦波，因此它們的振幅隨時間不斷變化。由於我們知道功率是電壓乘以電流（P = V * I），因此當兩個電壓和電流波形相互對齊時，將發生最大功率。也就是說，它們的峰值和零交叉點同時出現。當發生這種情況時，兩個波形被稱為“同相”。

交流電路中的三個主要部件可以通過定義電路的總阻抗來影響電壓和電流波形之間的關係，因此它們的相位差是電阻器，電容器和電感器。

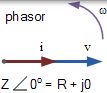
AC 電路的阻抗（Z）等於在 DC 電路中計算的電阻，阻抗以歐姆給出。對於 AC 電路，阻抗通常定義為電路元件產生的電壓和電流相量的比率。相量是以這樣的方式繪製的直線：通過其長度和相對於其他相量線的相位差來表示電壓或電流幅度，其相對於其他相量的角位置。

交流電路包含電阻和電抗，它們組合在一起以提供限制電路周圍電流的總阻抗（Z）。但是，一個交流電路中阻抗不等於所述電阻和電抗值歐姆的代數和為純電阻和電抗純是 90o 外的相位彼此。但是，我們可以用這個 90o 相位差為直角三角形的邊，稱為阻抗三角形，與阻抗為斜邊由勾股定理確定。

電阻，電抗和阻抗之間的這種幾何關係可以通過使用如圖所示的阻抗三角形在視覺上表示。

阻抗三角形

注意，阻抗，即電阻和電抗的向量和，不僅具有幅度（Z），而且還具有相角（θ），其表示電阻和電抗之間的相位差。還要注意，隨著頻率的變化，三角形會因電抗的變化而改變形狀，（X）。當然，電阻（R）將始終保持不變。

我們可以通過將阻抗三角形轉換為表示 AC 電路中的三個功率元件的功率三角形來進一步採取這一想法。歐姆定律告訴我們，在直流電路中，功率（P）（單位為瓦特）等於電流平方（I2）乘以電阻（R）。因此，我們可以將上面阻抗三角形的三邊乘以 I2 ，得到相應的冪三角形：

實際功率 P = I2 R 瓦，（W）

無功功率 Q = I2 X 伏安無功，（VAr）

視在功率 S = I2 Z 伏安，（VA）

交流電路中的實際功率

實際功率 （P），也稱為真功率或有功功率，在電路內執行“實際工作”。以瓦特為單位測量的實際功率定義了電路電阻部分所消耗的功率。然後，AC 電路中的實際功率（P）與 DC 電路中的功率 P 相同。因此就像直流電路一樣，它總是按 I2 * R 計算，其中 R 是電路的總電阻分量。

由於電阻不會在電壓和電流波形之間產生任何相量差異（相移），所有有用的功率都直接傳遞給電阻並轉換為熱量，光和工作。那麼電阻消耗的功率就是實際功率，這基本上是電路的平均功率。

為了找到實際功率的相應值，將均方根電壓和電流值乘以相位角的餘弦 θ，如圖所示。

實際功率 P = I2 R = V * I * cos（θ）瓦特，（W）

但由於它們在電阻電路中的電壓和電流之間沒有相位差，因此兩個波形之間的相移將為零（0）。然後：

交流電路中的實際功率

在實際功率（P）以瓦特為單位的情況下，電壓（V）以 rms 伏特為單位，電流（I）以 rms 安培為單位。

那麼實際功率是以瓦特為單位測量的 I2 * R 電阻元件，這是你在公用事業能量計上讀到的並且具有瓦特（W），千瓦（kW）和兆瓦（MW）的單位。注意實際功率，P 總是正的。

交流電路中的無功功率

無功功率 （Q）（有時稱為無功功率）是交流電路中消耗的功率，其不執行任何有用的工作但對電壓和電流波形之間的相移具有很大影響。無功功率與電感和電容產生的電抗有關，抵消了有功功率的影響。直流電路中不存在無功功率。

與完成所有工作的實際功率（P）不同，無功功率（Q）由於感應磁場和電容靜電場的產生和減少而從電路獲取功率，從而使真正的功率供電變得更難直接到電路或負載。

電感器在其磁場中儲存的功率試圖控制電流，而由電容器靜電場儲存的功率試圖控制電壓。結果是電容器“產生”無功功率並且電感器“消耗”無功功率。這意味著它們都消耗並向源返回電源，因此不會消耗任何實際功率。

為了找到無功功率，均方根電壓和電流值乘以相位角的正弦 θ，如圖所示。

無功功率 Q = I2 X = V * I * sin（θ）伏安無功，（VAr’s）

由於有一個 90o 的電壓和在純電抗的電流波形（無論是電感性或電容性）之間的相位差，由Sin乘以 V * I（θ）給出的垂直分量即 90o 外的相位與每個其他，所以：

交流電路中的無功功率

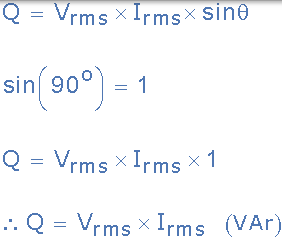
當無功功率（Q）以伏安無功時，電壓（V）以有效值電壓為單位，電流（I）以有效值安培為單位。

然後無功功率表示伏特和安培為 90 的產品o 外的相位彼此，但一般來說，可以有任意相位角，θ 的電壓和電流之間。

因此，無功功率是 I2 X 無功元件，其單位為伏安無功（VAr），千伏安無功（kVAr）和兆瓦安 - 無功（MVAr）。

交流電路中的視在功率

我們已經在上面看到，實際功率通過電阻消散，並且無功功率被提供給電抗。結果，由於電阻電阻和電抗元件之間的差異，電流和電壓波形不是同相的。

然後在實際功率（P）和無功功率（Q）之間存在數學關係，稱為復功率。施加到 AC 電路的均方根電壓 V 和流入該電路的均方根電流 I 的乘積稱為“伏安產品”（VA），給定符號 S，其大小通常稱為視在功率。

這個複數冪不等於加在一起的實數和無功功率的代數和，而是以伏安（VA）給出的 P 和 Q 的向量和。它是由功率三角形表示的複雜功率。伏安產品的均方根值通常被稱為視在功率，“顯然”這是電路消耗的總功率，即使完成工作的實際功率要少得多。

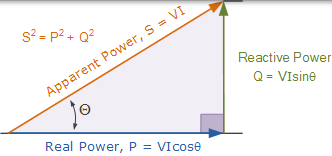
由於視在功率由兩部分組成，即以瓦特為單位的同相功率或實際功率的電阻功率和以伏安為單位的異相功率的無功功率，我們可以顯示向量加法這兩個功率元件以功率三角形的形式出現。功率三角形有四個部分：P，Q，S 和 θ。

在 AC 電路中構成功率的三個元件可以通過直角三角形的三個邊以圖形方式表示，其方式與先前的阻抗三角形大致相同。水平（相鄰）側表示電路實際功率（P），垂直（相對）側表示電路無功功率（Q），斜邊表示所示功率三角形的所得視在功率（S）。

交流電路的功率三角形

• 哪裡：
• P 是 I2 * R 或實際功率，以瓦特 W 為單位執行工作
• Q 是以伏安無功 VAr 測量的 I2 * X 或無功功率
• S 是以伏安（VA）為單位測量的 I2 * Z 或視在功率
• θ 是以度為單位的相位角。相角越大，無功功率越大
• Cos（θ）= P / S = W / VA =功率因數，pf
• Sin（θ）= Q / S = VAr / VA
• Tan（θ）= Q / P = VAr / W.

功率因數計算為實際功率與視在功率之比，因為該比率等於 cos（θ）。

交流電路中的功率因數

功率因數 cos（θ）是 AC 電路的重要部分，也可以用電路阻抗或電路功率表示。功率因數被定義為實際功率（P）與視在功率（S）的比率，並且通常表示為十進位制值，例如 0.95，或百分比：95％。

功率因數定義了電流和電壓波形之間的相角，I 和 V 是電流和電壓的均方根值的大小。注意，相角是電流相對於電壓的差，還是相對於電流的電壓無關緊要。數學關係如下：

交流電路的功率因數

我們先前所述，在一個純阻性電路，所述電流和電壓波形同相彼此所以所消耗的實際功率是相同的視在功率為相位差為零度（0o）。因此功率因數將是：

功率因數，pf = cos 0o = 1.0

也就是說，消耗的瓦數與消耗的伏安數相同，產生的功率因數為 1.0 或 100％。在這種情況下，它被稱為單位功率因數。

我們還表示上述，在純粹的電抗電路，電流和電壓波形是由 90 外的相位彼此o。由於相位差為 90 度（90o），功率因數將為：

功率因數，pf = cos 90o = 0

也就是說，消耗的瓦數為零，但仍然存在提供無功負載的電壓和電流。顯然，降低功率三角形的反應性 VAr 分量將導致 θ 減小將功率因數提高到 1，單位。還希望具有高功率因數，因為這使得電路的最有效使用將電流輸送到負載。

然後我們可以寫出實際功率，視在功率和電路功率因數之間的關係：

電流“滯後”電壓（ELI）的電感電路被稱為具有滯後功率因數，而電流“超前”電壓（ICE）的電容電路被認為具有超前功率因數。

Power Triangle 示例 No1

電感為 180mH，電阻為 35Ω 的繞線圈連線到 100V 50Hz 電源。計算：a）線圈的阻抗，b）電流，c）功率因數，和 d）消耗的視在功率。

同時繪製上述線圈的最終功率三角形。

給出的資料：R =35Ω，L = 180mH，V = 100V，ƒ= 50Hz。

（a）線圈的阻抗（Z）：

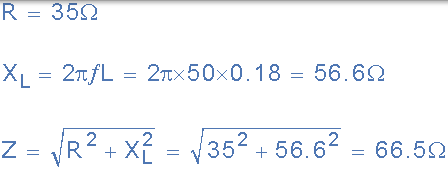
（b）線圈消耗的電流（I）：

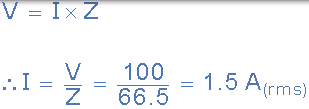
（c）功率因數和相位角 θ ：

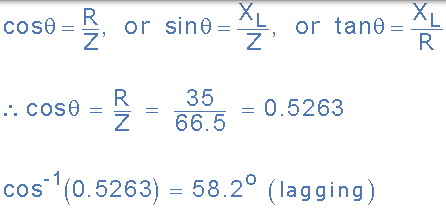
（d）線圈消耗的視在功率（S）：

（e）線圈的功率三角形：

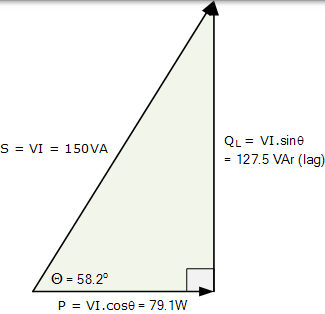
由於這個簡單示例的功率三角關係表明，在功率因數為 0.5263 或 52.63％時，線圈需要 150 VA 的功率才能產生 79 瓦的有用功。換句話說，在功率因數為 52.63％時，線圈需要大約 88％的電流來完成相同的工作，這是浪費大量的電流。

線上圈上增加一個功率因數校正電容器（例如 32.3uF），為了將功率因數增加到 0.95 或 95％，將大大降低線圈消耗的無功功率，因為​​這些電容器充當無功電流發電機，從而減少消耗的電流總量。

功率三角和功率因數總結

我們在這裡已經看到，交流電路中的三種電功率元件，即功率，無功功率和視在功率*可以用稱為功率三角形的三角形的三個邊來表示。由於這三個元素由“直角三角形”表示，它們的關係可以定義為：S2 = P2 + Q2，其中： P 是以瓦特為單位的實際功率（W），Q 是以伏安為單位的無功功率（VAr），S 是以伏安（VA）為單位的視在功率。

我們還看到，在交流電路中，量 cos（θ）被稱為功率因數。AC 電路的功率因數定義為電路消耗的實際功率（W）與同一電路消耗的視在功率（VA）之比。因此，這給出了：功率因數=實際功率/視在功率，或 pf = W / VA。

然後，電流和電壓之間產生的角度的餘弦是功率因數。通常，功率因數表示為百分比，例如 95％，但也可以表示為十進位制值，例如 0.95。

當功率因子等於 1.0（統一）或 100％時，即當實際消耗的功率等於電路的視在功率，電流和電壓之間的相位角為 0o 為：COS-1 （1.0）= 0o。當功率因數等於零（0）時，電流和電壓之間的相位角將為 90°， 因為：cos-1 （0）= 90o。在這種情況下，無論電路電流如何，AC 電路消耗的實際功率為零。

在實際的交流電路中，功率因數可以在 0 到 1.0 之間，具體取決於連線負載內的無源元件。對於感性電阻負載或電路（通常情況下），功率因數將“滯後”。在電容 - 電阻電路中，功率因數將是“領先的”。然後可以將 AC 電路定義為具有單位，滯後或超前功率因數。

具有朝向零（0）的值的較差功率因數將消耗浪費的功率，從而降低電路的效率，而具有接近一（1.0）或單位（100％）的功率因數的電路或負載將更有效。這是因為具有低功率因數的電路或負載需要比相同電路或負載更大的電流，其功率因數接近 1.0（單位）。