交流電路供電
AC 電路中的電阻消耗的電功率與電抗消耗的功率不同,因為電抗不會耗散能量
在直流電路中,所消耗的功率僅僅是直流電壓乘以直流電流的乘積,單位為瓦特。但是,對於具有電抗元件的交流電路,我們必須以不同方式計算消耗功率。
電功率是在電路中消耗能量的“速率”,因此所有電氣和電子部件和裝置對它們可以安全處理的電功率量具有限制。例如,1/4 瓦電阻器或 20 瓦放大器。
電功率可以是隨時間變化的 DC 量或 AC 量。在任何時刻電路中的功率量稱為*瞬時功率,*並且由眾所周知的功率關係等於伏特乘以安培(P = V * I)給出。因此,一瓦特(即每秒一焦耳的能量消耗速率)將等於一伏安 1 安培的伏安產品。
然後,由電路元件吸收或提供的功率是元件上的電壓 V 和流過它的電流 I 的乘積。因此,如果我們有一個電阻為 R 歐姆的直流電路,則電阻器以瓦特為單位消耗的功率由以下任何通用公式給出:
電力
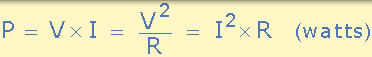
其中: V 是直流電壓,I 是直流電流,R 是電阻值。
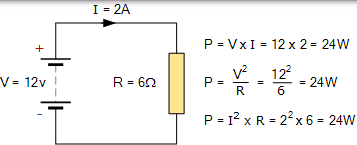
因此,當電壓和電流都存在時,電路內的電源才會出現,即沒有開路或閉路條件。考慮以下標準電阻直流電路的簡單示例:
直流電阻電路
交流電路中的電源
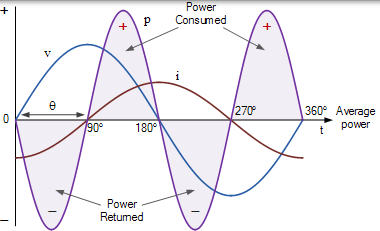
在 DC 電路中,電壓和電流通常是恆定的,不隨時間變化,因為沒有與電源相關的正弦波形。然而,在 AC 電路中,電壓,電流和因此功率的瞬時值不斷變化受到電源的影響。因此我們無法以與直流電路相同的方式計算交流電路中的功率,但我們仍然可以說功率(p)等於電壓(v)乘以安培(i)。
另一個重點是交流電路包含電抗,因此由於元件產生的磁場和/或電場存在功率分量。結果是,與純電阻元件不同,當正弦波形經過一個完整的週期迴圈時,該功率被儲存然後返回到電源。
因此,電路吸收的平均功率是儲存的功率和在一個完整週期內返回的功率之和。因此,電路平均功耗將是一個完整週期內瞬時功率的平均值,瞬時功率 p 定義為瞬時電壓 v 乘以瞬時電流 i。請注意,由於正弦函式是週期性的和連續的,因此在所有時間內給出的平均功率將與在單個週期內給出的平均功率完全相同。
我們假設電壓和電流的波形都是正弦波,所以我們記得:
正弦電壓波形
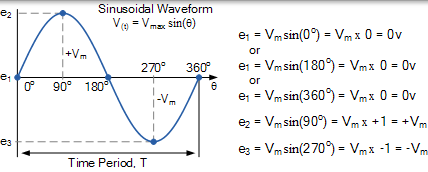
由於瞬時功率是任何時刻的功率,因此:

應用三角積的產品 - 總和身份:

和 θ =θv -θi (電壓和電流波形之間的相位差)進入上式得出:
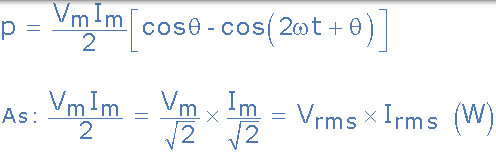
其中 V 和 I 分別是正弦波形的均方根(rms)值,v 和 i,θ 是兩個波形之間的相位差。因此我們可以將瞬時功率表達為:
瞬時交流功率方程

該等式向我們表明,瞬時交流電源具有兩個不同的部分,因此是這兩個術語的總和。第二項是時變正弦曲線,由於該項的 2ω 部分,其頻率等於電源角頻率的兩倍。然而,第一項是常數,其值僅取決於電壓,(V)和電流之間的相位差 θ,(I)。
由於隨著時間的推移瞬時功率隨著正弦曲線的輪廓而不斷變化,這使得難以測量。因此,使用平均值或平均值來計算資料更方便,更容易。因此,在固定數量的週期內,正弦波的瞬時功率的平均值簡單地給出:
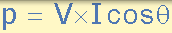
其中 V 和 I 是正弦曲線有效值,而 θ (Theta)是電壓和電流之間的相角。功率單位是瓦特(W)。
如圖所示,電路中消耗的交流功率也可以從電路的阻抗(Z)中找到,該電阻使用電壓 Vrms 或流過電路的電流 Irms。
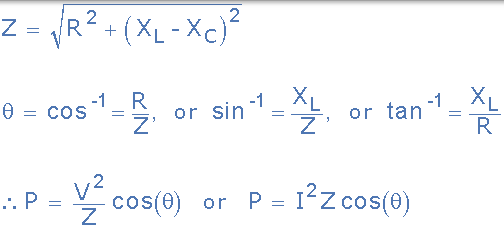
交流電源示例 No1
50Hz 正弦電源的電壓和電流值分別如下:vt = 240 sin(ωt+ 60o)伏特和 it = 5 sin(ωt-10o)安培。找出瞬時功率的值和電路吸收的平均功率。
從上面看,電路吸收的瞬時功率如下:

應用上面的三角標識規則給出:

然後將平均功率計算為:
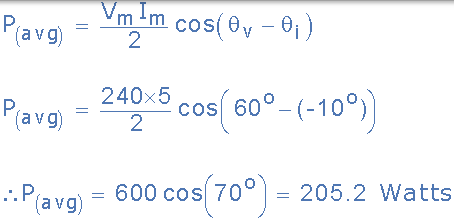
你可能已經注意到,205.2 瓦的平均功率值也是瞬時功率 p(t) 的第一項值,因為該第一項常數值是源和負載之間的平均或平均能量變化率。
純電阻電路中的交流電源
到目前為止,我們已經看到,在直流電路中,功率等於電壓和電流的乘積,這種關係對於純電阻的交流電路也是如此。電阻器是消耗能量的電子器件,電阻器中的功率由 p = VI = I2 R = V2 / R 給出。這種力量總是積極的。
考慮以下純電阻(即無限電容,C =∞和零電感,L = 0)電路,其電阻連線到交流電源,如圖所示。
純電阻電路
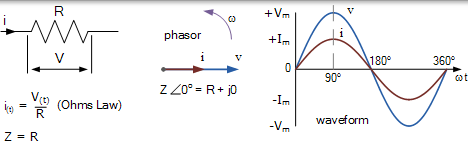
當純電阻器連線到正弦電壓電源時,流過電阻器的電流將與電源電壓成比例地變化,即電壓和電流波形彼此“同相”。由於電壓波形和電流波形之間的相位差為 0o,導致 COS 相位角 0o 將等於 1。
然後電阻器消耗的電能由下式給出:
純電阻器中的電源
由於電壓和電流波形是同相的,即兩個波形同時達到其峰值,同時也通過零,上面的功率方程式降低到恰好:V * I。因此,通過將兩個波形相乘得到伏安產品,可以找到任何瞬間的功率。這稱為“實際功率”,(P)以瓦特,(W),千瓦(kW),兆瓦(MW)等為單位測量。
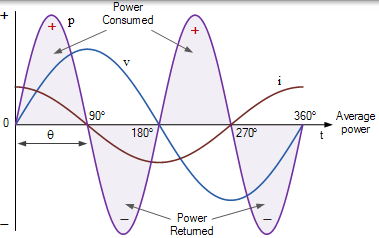
用於純電阻的交流電源波形
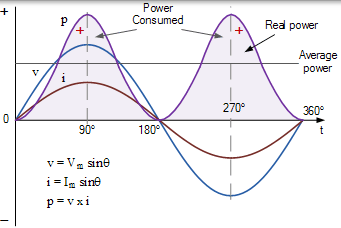
該圖顯示了電壓,電流和相應的功率波形。由於電壓和電流波形都是同相的,因此在正半週期期間,當電壓為正時,電流也為正,因此功率為正,正為正,正為正等於正。在負半週期期間,電壓為負,因此為導致功率為正的電流,負為負的時間等於正。
然後在純電阻電路中,電流在電流流過電阻器時消耗,並給出如下:P = V * I = I2 R 瓦。注意,V 和 I 都可以是它們的 rms 值,其中:V = I * R,I = V / R.
純電感電路中的交流電源
在 L Henries 的純電感(即無限電容,C =∞和零電阻,R = 0)電路中,電壓和電流波形不同相。每當向純電感線圈施加變化的電壓時,由於其自感,線圈產生“後”電動勢。這種自感反對並限制了線圈中流動電流的任何變化。
該反電動勢的影響是電流不能立即通過線圈與施加的電壓同相地增加,導致電流波形在電壓之後的某個時間達到其峰值或最大值。結果是,在純電感電路中,電流總是在電壓後滯後(ELI)90o (π/ 2),如圖所示。
純電感電路
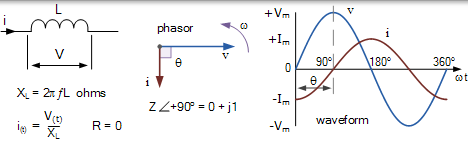
上面的波形顯示了純電感線圈上的瞬時電壓和瞬時電流隨時間的變化。最大電流 Imax 出現在電壓的最大(峰值)值之後的一個週期的一個完整四分之一(90o)處。這裡的電流被示出為具有在電壓週期的開始它的負最大值和通過零點時的電壓波形是在其最大值在 90 增加至其正的最大值o。
因此,當電壓和電流波形不再上升和下降一起,而是 90 的相移o (π/ 2)線上圈中被引入,則電壓和電流波形是“外的相”與每個另外,電壓導致電流達到 90o。由於電壓波形和電流波形之間的相位差是 90o,則相位角導致在 COS 90o = 0。
因此,純電感器儲存的電功率 QL 由下式給出:
純電感中的實際功率
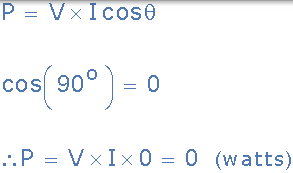
顯然,純電感器不消耗或消耗任何實際功率或真實功率,但由於我們同時具有電壓和電流,因此在表示式中使用 cos(θ):P = V * I * cos(θ)用於純電感器不再有效。在這種情況下,電流和電壓的乘積是虛功率,通常稱為“無功功率”,(Q)以伏安無功,(VAr),Kilo-voltamperes 無功(KVAr)等測量。
Voltamperes 反應,VAr 不應與瓦特混淆,(W)用於實際功率。無功表示是 90 伏特和安培的產物o 外的相位彼此。為了在數學上識別無功平均功率,使用正弦函式。然後,電感器中平均無功功率的等式變為:
純電感器中的無功功率
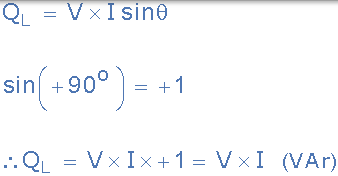
與實際功率(P)一樣,無功功率(Q)也取決於電壓和電流,但也取決於它們之間的相位角。因此,所施加的電壓的乘積,並且是 90 的電流的組成部分o 如圖外的與電壓同相。
用於純電感的交流電源波形

在 0 的角度之間的電壓波形的正半o 和 90o,而電源電壓是正的電感電流是負的。因此,伏特和安培產品給出負功率,負值乘以正值等於負值。在 90o 和 180o 之間,電流和電壓波形均為正值,從而產生正功率。該正功率表示線圈消耗來自電源的電能。
在 180° 和 270° 之間的電壓波形的負半部分中,存在負電壓和正電流,表示負電源。該負功率表示線圈將儲存的電能返回到電源。在 270o 和 360o 之間,電感器電流和電源電壓都是負的,從而產生正功率週期。
然後在電壓波形的一個完整週期期間,我們有兩個相同的正負脈衝功率,其平均值為零,因此沒有實際功率用完,因為功率交替地流入和流出源。這意味著純電感器在一個完整週期內所消耗的總功率為零,因此電感器無功功率不會執行任何實際工作。
純電容電路中的交流電源
C 法拉的純電容(即零電感,L = 0 和無限電阻,R =∞)電路具有延遲其兩端電壓變化的特性。電容器以電場的形式儲存電介質中的電能,因此純電容器不會消耗任何能量,而是儲存它。
在純電容電路中,電壓不能與電流同相增加,因為它需要首先“充電”電容器板。這導致電壓波形在電流之後的某個時間達到其峰值或最大值。結果是,在純電容電路中,電流總是“超前”(ICE)電壓 90o (ω/ 2),如圖所示。
純電容電路
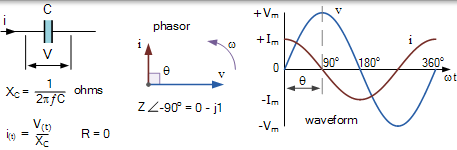
波形向我們顯示純電容器上的電壓和電流隨時間的變化。最大電流 Im 在電壓的最大(峰值)值之前的一個週期(90o)的四分之一處發生。這裡的電流被示出為具有在電壓週期的開始它的正的最大值和通過零點,減少到其負的最大值,當電壓波形是在在 90 其最大值o。相反的相移到純電感電路。
因此,對於純電容電路,相位角 θ= -90o 和電容器中平均無功功率的等式變為:
純電容器中的無功功率
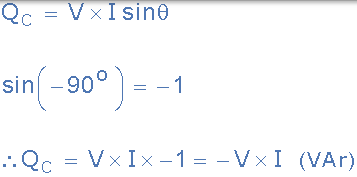
其中-V * I * sin(θ)是負正弦波。此外,容性無功功率的符號是 QC, 具有相同的測量單位,伏安無功(VAR)與電感器相同。然後我們可以看到,就像上面的純電感電路一樣,純電容器不會消耗或耗散任何真實或真實的功率,P。
用於純電容器的交流電源波形
在 0 的角度之間的電壓波形的正半o 和 90o,無論是電流和電壓波形是在產生正功率值正被消耗。在 90o 和 180o 之間,電容器電流為負,電源電壓仍然為正。因此,伏安產品給出負功率,負值乘以正值等於負值。該負功率表示線圈將儲存的電能返回到電源。
在 180° 和 270° 之間的電壓波形的負半部分中,電容器電流和電源電壓都是負值,導致正功率週期。這段正功率表明線圈正在消耗電源的電能。在 270o 和 360o 之間,存在負電壓和正電流,再次表示負電源。
然後,在電壓波形的一個完整週期期間,存在與純電感電路相同的情況,因為我們具有兩個相同的正負脈衝,其平均值為零。因此,從電源輸送到電容器的功率恰好等於電容器返回到電源的功率,因此沒有實際功率耗盡,因為功率交替地流入和流出源。這意味著純電容器在一個完整週期內所消耗的總功率為零,因此電容器無功功率不會執行任何實際工作。
電力例項 No2
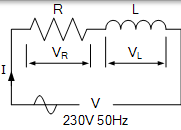
電阻為 30 歐姆,電感為 200mH 的電磁線圈連線到 230VAC,50Hz 電源。計算:(a)螺線管阻抗,(b)螺線管消耗的電流,(c)電流和施加電壓之間的相角,以及(d)螺線管消耗的平均功率。
給出的資料:R =30Ω,L = 200mH,V = 230V,ƒ= 50Hz。
(a)電磁線圈的阻抗(Z):
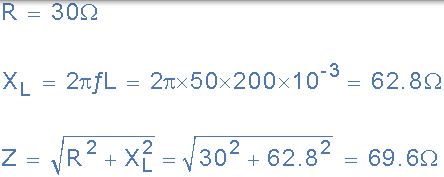
(b)電磁線圈消耗的電流(I):
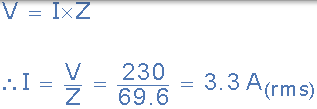
(c)相位角 θ:
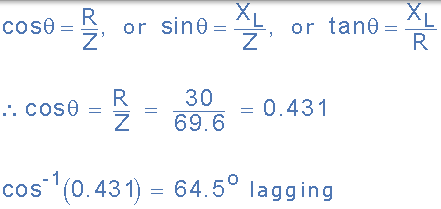
(d)電磁線圈消耗的平均交流功率:

交流電力總結
我們在這裡看到,在交流電路中,在純無源電路中流動的電壓和電流通常是異相的,因此,它們不能用於完成任何實際工作。我們還看到,在直流(DC)電路中,電功率等於電壓乘以電流,或 P = V * I,但我們無法以與交流電路相同的方式計算它,因為我們需要考慮到任何相位差異。
在純電阻電路中,電流和電壓都是同相的,並且所有電功率都被電阻消耗,通常作為熱量。結果,沒有電力返回到電源或電路。
然而,在一個純電感或包含電抗純電容電路,(X)中的電流將超前或滯後正好 90 的電壓o (相位角),因此功率都儲存並返回到源。因此,在一個完整週期迴圈中計算的平均功率將等於零。
電阻(R)消耗的電功率稱為真功率或實功率,簡單地通過將均方根電壓與均方根電流相乘得到。由電抗儲存的功率(X)被稱為無功功率,並且通過將它們之間的相角的電壓,電流和正弦相乘來獲得。
相角的符號是 θ(θ),並且表示 AC 電路相對於與電路中的電流流動相反的總無功阻抗(Z)的低效率。