相量圖和相量代數

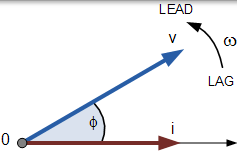
相量圖是一種表示兩個或多個交變數之間的大小和方向關係的圖形方式

相同頻率的正弦波形可以在它們之間具有相位差，其表示兩個正弦波形的角度差。此外，術語超前和滯後以及同相和異相通常用於表示一個波形與另一個波形的關係，其中廣義正弦表示式如下： A(t) = Am sin(ωt±Φ) 表示時域形式的正弦曲線。

但是，當以這種方式以數學方式呈現時，有時難以使兩個或更多個正弦波形之間的角度或相量差異視覺化。克服該問題的一種方法是通過使用相量圖以空間或相量域形式在圖形上表示正弦曲線，並且這通過旋轉向量方法實現。

基本上，旋轉向量，簡稱為相量，是縮放線，其長度表示具有在某個時間點“凍結”的幅度（“峰值幅度”）和方向（“相位”）的 AC 量。

相量是在一端具有箭頭的向量，其部分地表示向量（ V 或 I） 的最大值，並且部分地表示旋轉的向量的末端。

通常，假設向量在一端圍繞稱為“原點”的固定零點旋轉，而表示數量的箭頭端在一個角速度下以逆時針方向自由旋轉。向量的這種逆時針旋轉被認為是正旋轉。同樣，順時針旋轉被認為是負旋轉。

儘管術語向量和相量都用於描述本身具有幅度和方向的旋轉線，但兩者之間的主要區別在於向量幅度是正弦波的峰值，而相量幅度是 RMS 值的正弦曲線。在兩種情況下，相位角和方向保持不變。

任何時刻的交變數的相位可以用相量圖表示，因此相量圖可以被認為是“時間函式”。可以通過以 ω=2π 的角速度旋轉的單個向量來構造完整的正弦波，其中 f 是波形的頻率。然後，相量是具有“幅度”和“方向”的量。

通常，當構造相量圖時，總是假設正弦波的角速度 ω 以 rad/sec 為單位。考慮下面的相量圖。

正弦波形的相量圖

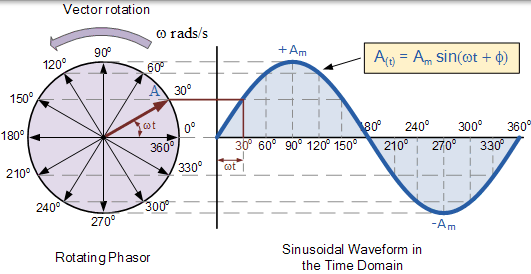
當單個向量沿逆時針方向旋轉時，其在 A 點的尖端將進行一個 360o 或 2π 的完整旋轉，代表一個完整的迴圈。如果其移動尖端的長度在時間上以不同的角度間隔傳遞到如上所示的曲線圖，則將在零時間從左側開始繪製正弦波形。沿水平軸的每個位置表示從零時間開始經過的時間，t = 0。當向量是水平時，向量的尖端表示 0°、180° 和 360o。

同樣地，當向量的前端垂直它所代表的正峰值 Am 在 90o 或 π/ 2 時，以及負峰值 -Am 在 270o 或 3π/ 2。然後波形的時間軸表示相量移動的角度或弧度。因此，我們可以說相量代表旋轉向量的縮放電壓或電流值，該旋轉向量在某個時間點（ t） 被“凍結”，在上面的例子中，是 30° 的角度。

有時，當我們分析交流波形時，我們可能需要知道相量的位置，表示某個特定時刻的交變數，特別是當我們想要比較同一軸上的兩個不同波形時，例如，電壓和電流。我們在上面的波形中假設波形在時間 t = 0 開始，相應的相角為度或弧度。

但是，如果第二個波形開始於此零點的左側或右側，或者我們希望以相量符號表示兩個波形之間的關係，那麼我們將需要考慮波形的這個相位差 Φ。請考慮上一個相位差教程中的下圖。

正弦波形的相位差

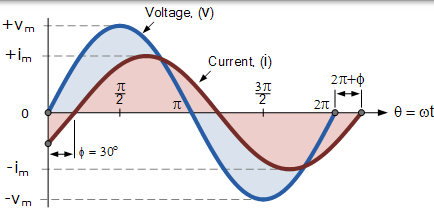
定義這兩個正弦量的廣義數學表示式將寫為：

$$ \begin{array} { l } { \mathrm { V } _ { ( \mathrm { t } ) } = V _ { \mathrm { m } } \sin ( \omega \mathrm { t } ) } \\ { \mathrm { i } _ { ( \mathrm { t } ) } = \mathrm { I } _ { \mathrm { m } } \sin ( \omega \mathrm { t } - \phi ) } \end{array} $$

電流 i 滯後於電壓 v 的角度為 Φ，在上面的例子中，是 30o。因此，表示兩個正弦量的兩個相量之間的差異是角度 Φ，並且得到的相量圖將是，

正弦波形的相量圖

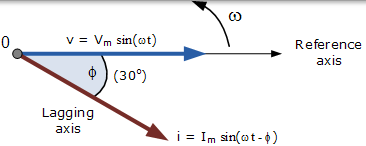
對應於水平軸上的時間零（ t = 0） 繪製相量圖。相量的長度與繪製相量圖的瞬間電壓（V）和電流（I）的值成比例。當兩個相量如前所述沿逆時針方向旋轉時，電流相量滯後電壓相量角度 Φ，因此角度 Φ 也在相同的逆時針方向上測量。

但是，如果波形在時間 t = 30o 時凍結，相應的相量圖將如右圖所示。由於兩個波形具有相同的頻率，因此電流相量再次落後於電壓相量。

然而，由於電流波形現在在此時刻穿過水平零軸線，我們可以使用電流相量作為我們的新參考，並正確地說電壓相量將電流相量“超前”角度 Φ。無論哪種方式，一個相量被指定為參考相量，並且所有其他相量將相對於該參考超前或滯後。

相量相加

有時在研究正弦曲線時需要將兩個交流波形加在一起，例如在 AC 串聯電路中，它們彼此不同相。如果它們是同相的，則沒有相移，那麼它們可以以與 DC 值相同的方式加在一起，以找到兩個向量的代數和。例如，如果分別為 50 伏和 25 伏的兩個電壓同相，則它們將以相加的形成 75 伏（50 + 25）的一個電壓。

然而，如果它們不同相，即它們不具有相同的方向或起始點時，需要將它們之間的相位角考慮進來，用向量圖通過平行四邊形法則來決定它們的相量和或向量和。

考慮兩個交流電壓，V1 具有 20 伏的峰值電壓，V2 為 30 伏的峰值電壓，其中 V1 超前 V2 60o。兩個電壓的總電壓 VT 可以通過首先畫出表示兩個向量的向量圖，然後構造一個平行四邊形，其中兩個邊是電壓，V1 和 V2。如下所示。

兩個相量的相量加法

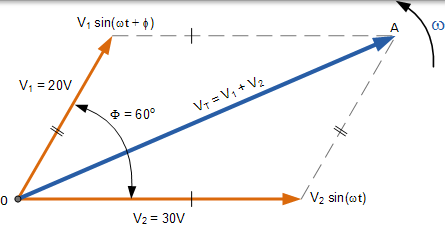
通過繪製兩個相量以縮放到方格紙上，通過測量從零點到交叉點的對角線的長度（稱為合成向量），可以很容易地找到 V1 + V2 它們的相量和 - 線 0-A。這種圖形方法的缺點是在繪製相量尺時需要耗費時間。

此外，雖然此圖形方法提供的答案對於大多數目而言足夠準確，但如果未精確繪製或未按比例繪製，則可能會產生錯誤。然後，通過分析方法確保始終獲得正確答案的一種方法。

在數學上將兩個電壓加在一起，我們可以通過首先找到它們的垂直和水平方向，然後由此我們可以計算得到的合成向量 VT 的“垂直”和“水平”分量。這種使用餘弦和正弦規則來找到該結果值的分析方法通常稱為矩形形式。

在矩形形式中，相量被分成實部 x 和虛部 y，形成廣義表示式 Z = x±jy。 （我們將在下一個教程中更詳細地討論這個問題）。然後，這給出了一個表示正弦電壓幅度和相位的數學表示式：

複雜正弦波的定義

$$ V _ { m } = \cos ( \phi ) + j V _ { m } ( \sin \phi ) $$

因此，使用先前的廣義表示式將兩個向量 A 和 B 相加，如下所示，

$$ \begin{array} { l l } { A = x + j y } & { B = w + j z } \\ { A + B = ( x + w ) + j ( y + z ) } \end{array} $$

使用矩形形式的相量加法

電壓 V2 沿著水平軸的參考方向，幅值為 30 V，然後它具有水平分量但沒有垂直分量。

• 水平分量 = 30 cos 0o = 30 伏
• 垂直分量 = 30 sin 0o = 0 伏

然後，這給出了電壓 V2 的矩形表示式 ： 30 + j0

電壓，20 伏的 V1 超前 V2 60o，然後它具有如下的水平和垂直分量。

• 水平分量 = 20 cos 60o = 20 x 0.5 = 10 伏

• 垂直分量 = 20 sin 60o = 20 x 0.866 = 17.32 伏

• • 然後，這給出了電壓 V1 的矩形表示式 ： 10 + j17.32

通過如下將水平和垂直分量加在一起得到合成電壓 VT，

• VHorizontal = V1 和 V2 的實部之和 = 30 + 10 = 40 伏
• VVertical = V1 和 V2 的虛部之和 = 0 + 17.32 = 17.32 伏

現在，無論是實數和虛數值已經計算出電壓的幅度，VT 是通過簡單地使用畢達哥拉斯定理來計算，

$$ \mathrm { V } _ { \mathrm { T } } = \sqrt { 實部 ^ { 2 } + 虛部 ^ { 2 } } \\ \mathrm { V } _ { \mathrm { T } } = \sqrt { 40 ^ { 2 } + 17.32 ^ { 2 } } $$

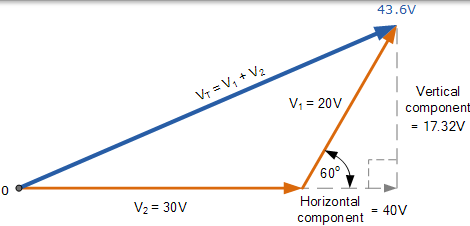
然後得到的相量圖將是：

VT 的 結果值

相量減法

相量減法與上述矩形加法非常相似，除了此時向量差是 V1 和 V2 的兩個電壓之間的平行四邊形的另一個對角線，如圖所示。

兩個相量的向量減法

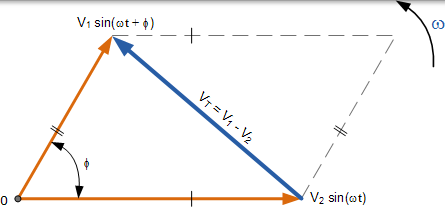
這次不是將水平和垂直分量加在一起，而是將相減。

$$ \begin{array} { l l } { A = x + j y } & { B = w + j z } \\ { A - B = ( x - w ) + j ( y - z ) } \end{array} $$

三相相量圖

以前我們只研究了單相交流波形，其中單個多匝線圈在磁場內旋轉。但如果三個具有相同匝數的線被放置在相同的轉子軸上，彼此相隔 120o 電角度，將產生的三相電壓電源。

平衡的三相電壓源由三個單獨的正弦電壓組成，這些電壓在幅度和頻率上都相等，但彼此相位差正好為 120o 電角度。

標準做法是將三個階段的顏色編碼為紅色，黃色和藍色，以識別每個單獨的相，紅色相作為參考相。三相供應的正常旋轉順序是紅色，接著是黃色，接著是藍色，（ R，Y，B）。

與上面的單相相量一樣，表示三相系統的相量也圍繞中心點沿逆時針方向旋轉，如標記為 ω 的箭頭所示，以 rad/s 為單位。三相平衡星形或三角形連線系統的相量如下所示。

三相相量圖

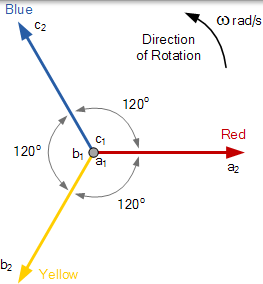
相電壓的大小都相等，但相位角只有不同。線圈的三個繞組在點 a1，b1 和 c1 處連線在一起，以產生用於三個單獨相的共同中性連線。然後，如果將紅相作為參考相，則可以相對於公共中性點定義每個單獨的相電壓。

三相電壓方程

$$ \begin{aligned} \text { RedPhase: } & \mathrm { V } _ { \mathrm { RN } } = \mathrm { V } _ { \mathrm { m } } \sin \theta \\ \text { Yellow Phase: } & \mathrm { V } _ { \mathrm { YN } } = \mathrm { V } _ { \mathrm { m } } \sin \left( \theta - 120 ^ { \circ } \right) \\ \text { Blue Phase: } \mathrm { V } _ { \mathrm { BN } } & = \mathrm { V } _ { \mathrm { m } } \sin \left( \theta - 240 ^ { \circ } \right) \\ or, \mathrm { V } _ { \mathrm { BN } } & = \mathrm { V } _ { \mathrm { m } } \sin \left( \theta + 120 ^ { \circ } \right) \end{aligned} $$

如果將紅相電壓 VRN 作為前面所述的參考電壓，則相序將為 R - Y - B，因此黃相中的電壓滯後 VRN 120o，藍相中的電壓滯後 VYN 也是 120o。但我們也可以說藍相電壓 VBN 將紅相電壓 VRN 超前 120o。

關於三相系統的最後一點。由於三個單獨的正弦電壓彼此之間具有固定的關係 120o 相移，因此它們被稱為平衡，因為在一組平衡的三相電壓中，它們的相量和總是為零： Va + Vb + Vc = 0

相量圖摘要

然後總結一下關於相量圖的重點知識。

最簡單的來說，相量圖是旋轉向量在水平軸上的投影，表示瞬時值。由於可以繪製相量圖以表示任何時刻，因此任何角度，交變數的參考相量總是沿著正 x 軸方向繪製。

• 向量，相量和相量圖僅適用於正弦交流交流量。
• 相量圖可用於在任何時刻表示兩個或更多個固定的正弦量。
• 通常，參考相量沿水平軸繪製，並且在該時刻繪製其他相量。所有相量均參考水平零軸繪製。
• 可以繪製相量圖來表示兩個以上的正弦曲線。它們可以是電壓，電流或其他一些交變數，但它們的頻率必須相同。
• 所有相量都沿逆時針方向旋轉。據說參考相量之前的所有相量都是超前，而參考相量後面的所有相量都被稱為滯後。
• 通常，相量的長度表示正弦量的 rms 值而不是其最大值。
• 由於向量的速度不同，不同頻率的正弦波不能在相同的相量圖上表示。在任何時刻，它們之間的相位角將是不同的。
• 可以將兩個或更多個向量一起新增或減去，併成為單個向量，稱為結果向量。
• 向量的水平邊等於實數或 x 向量。向量的垂直邊等於虛數或 y 向量。合成的直角三角形的斜邊等同於合成向量。
• 在三相平衡系統中，每個相位移相 120°。

在下一個關於 AC 理論的教程中，我們將把正弦波形表示為矩形形式的複數，極性形式和指數形式。