交流電感和電感電抗

電流通過交流電感時的抵抗稱為感應電抗，它取決於供電頻率。

電感器和扼流圈基本上是線圈，它們纏繞在中空管（空心芯）上或纏繞在一些鐵磁材料（鐵芯）周圍，以增加它們的感應值，這稱為電感。

電感器以磁場的形式儲存它們的能量，該磁場是在電感器的端子上施加電壓時產生的。流過電感器的電流的增長不是瞬時的，而是由電感器自身的自感應或反電動勢值決定的。然後對於電感線圈，該反電動勢電壓 VL 與流過它的電流的變化率成比例。

該電流將繼續上升，直到達到其最大穩態狀態，該狀態大約為五個時間常數，此時該自感應反電動勢已衰減為零。此時，穩態電流流過線圈，不再產生反電動勢以抵抗電流，因此，線圈更像是一個短路，允許最大電流流過它。

然而，在包含 AC 電感的交流電路中，通過電感器的電流與穩態 DC 電壓的行為非常不同。現在在交流電路中，流過線圈繞組的電流的抵抗不僅取決於線圈的電感，而且還取決於施加的電壓波形的頻率。

對流過 AC 電路中的線圈的電流的實際抵抗由線圈的 AC 電阻確定，該 AC 電阻由複數表示。但是為了區分 DC 電阻值和 AC 電阻值（也稱為阻抗），使用術語電抗。

與電阻類似，電抗以歐姆為單位，但是用符號 X 來區別於純電阻 R 值，並且因為所討論的元件是電感器，電感器的電抗稱為電感電抗 XL 以歐姆為單位。它的值可以從公式中找到。

感應電抗

$$ X _ { L } = 2 \pi f L $$

其中： XL 是以歐姆為單位的電感電抗， ƒ 是以赫茲為單位的頻率，L 是線圈的電感，單位為 Henry。

我們還可以用弧度定義感抗，其中 ω 等於 2πf。

$$ X _ { L } = \omega L $$

因此，無論何時向電感線圈施加正弦電壓，反電動勢都會阻止流過線圈的電流的上升和下降，以及純電感線圈，其電阻或損耗為零，此阻抗（可能是一個複數）等於其感應電抗。電抗也可以用向量來表示，因為它具有幅度和方向（角度）。考慮下面的電路。

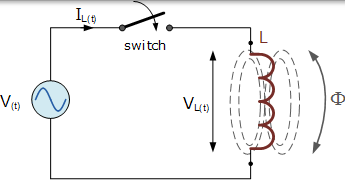
具有正弦電源的交流電感

此電路由一個 L 亨的純電感的，橫跨在以下表示式給出的正弦電壓上連線： V(t) = VmaxsinωT。當開關閉合時，該正弦電壓將導致電流流動並從零上升到其最大值。電流的這種上升或變化將線上圈內引起磁場，這反過來將抵抗或限制電流的這種變化。

但是，在電流有時間達到其在 DC 電路中的最大值之前，電壓會改變極性，從而導致電流改變方向。在另一個方向上的這種變化再次被線上圈中的自感反電動勢延遲。在只包含純電感的電路中，電流被延遲 90o。

施加的電壓在電流達到其最大正值之前的一個週期的四分之一（ 1 / 4f）內達到其最大正值，換句話說，施加到純電感電路的電壓將超前電流的四分之一週期或 90o，如下所示。

交流電感的正弦波形

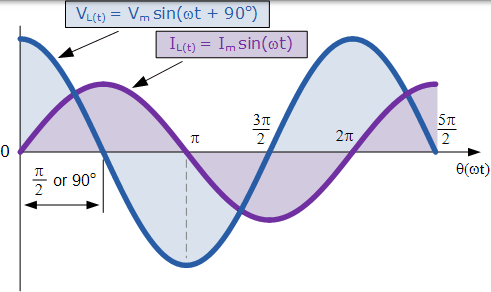
這種效應也可以用相量圖表示，在純電感電路中電壓超前電流 90o。但是，使用該電壓作為我們的參考的話，我們也可以說，電流滯後於電壓週期的四分之一或 90o，如示於下面的向量圖。

交流電感的相量圖

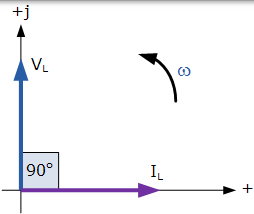
因此，對於純粹的無損耗電感器，VL 超前 IL 90o，或者我們可以說 IL 滯後 VL 90o。

頻率對感應電抗的影響

當一個 50Hz 的電源接在交流電感時，電流將有 90o 延遲，如先前所描述那樣。並且在每個半週期結束電壓反轉極性之前，電流將達到峰值，即電流在 T 秒內達到最大值。

如果我們現在向線圈施加相同峰值電壓的 100Hz 電源，電流仍將延遲 90o，但其最大值將低於 50Hz 時的值，因為頻率增加所以達到其最大值所需的時間已減少，現在只有 1/2 T 秒達到其峰值。而且，由於頻率的增加，線圈內的通量的變化率也增加。

然後根據上述感抗電抗等式，可以看出，如果頻率或電感增加，則線圈的總感應電抗值也會增加。隨著頻率增加並接近無窮大，電感器電抗，因此其阻抗也會朝向無窮大增加，就像開路一樣。

同樣地，當頻率接近零或 DC 時，電感器電抗也將減小到零，其作用類似於短路。這意味著感應電抗與頻率成正比，並且在低頻時具有較小值，在較高頻率處具有較高值，如圖所示。

感性電抗 vs 頻率

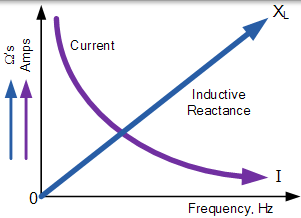
因此一個電感器的電抗隨著其兩端的頻率增加而感抗增加。感抗與頻率成正比（ XL ∝ ƒ），在電感器中產生的反電動勢等於其電感乘以的電流變化的電感器中的速率。

此外，隨著頻率的增加，流過電感器的電流的值也會降低。

我們可以將非常低和非常高的頻率對純 AC 電感的電抗的影響表示如下：

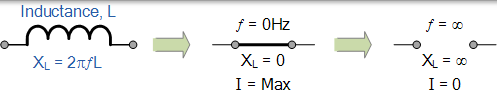
在包含純電感的交流電路中，適用以下公式，

$$ \text { Current, I } = \frac { \text { Voltage } } { \text { Opposition to current flow } } = \frac { \mathrm { V } } { \mathrm { X } _ { \mathrm { L } } } $$

那麼我們是如何得出這個等式的呢？ 電感中的自感電動勢由法拉第定律確定，該法則由於電流的變化率而在電感器中產生自感應效應，並且感應電動勢的最大值將對應於最大變化率。然後電感線圈中的電壓如下：

$$ \mathrm { V } _ { \mathrm { L } ( \mathrm { t } ) } = \mathrm { L } \frac { \mathrm { di } _ { \mathrm { L } ( \mathrm { t } ) } } { \mathrm { dt } } $$

假如 $\mathrm { i } _ { \mathrm { L } ( \mathrm { t } ) } = \mathrm { I } _ { \max } \sin ( \omega \mathrm { t } )$ ，那麼

$$ \begin{aligned} \mathrm { V } _ { \mathrm { L } ( t ) } & = \mathrm { L } \frac { \mathrm { d } } { \mathrm { dt } } \mathrm { I } _ { \max } \sin ( \omega \mathrm { t } + \theta ) \\ & = \omega \mathrm { L } \mathrm { I } _ { \max } \cos ( \omega \mathrm { t } + \theta ) \end{aligned} $$

那麼交流電感兩端的電壓定義如下：

$$ \mathrm { V } _ { \mathrm { L } } = \omega \mathrm { L } \mathrm { I } _ { \max } \sin \left( \omega \mathrm { t } + 90 ^ { \circ } \right) $$

其中： VL =IωL，它是電壓幅度， θ= + 90o，它是電壓和電流之間的相位差或相位角。

相量域中

在相量域中，線圈兩端的電壓如下：

$$ \mathrm { V } _ { \mathrm { L } } = \mathrm { j } \omega \mathrm { L } \mathrm { I } $$

其中，$j \omega \mathrm { L } = \mathrm { j } \mathrm { X } _ { \mathrm { L } } = 2 \pi f \mathrm { L } = \mathrm { IMPED } \mathrm { ANCE } , \mathrm { Z }$

在極座標形式，這可以寫為： XL ∠90o 其中： $$ \mathrm { X } _ { \mathrm { L } } \angle \theta = \frac { \mathrm { V } _ { \mathrm { L } } \angle + 90 ^ { \circ } } { \mathrm { I } _ { \mathrm { L } } \angle 0 ^ { \circ } } $$

$$ \mathrm { X } _ { \mathrm { L } } \angle \theta = \mathrm { j } \omega \mathrm { L } = 0 + \mathrm { j } \mathrm { X } _ { \mathrm { L } } = \omega \mathrm { L } \angle + 90 ^ { \circ } = \mathrm { Z } \angle + 90 ^ { \circ } $$

串聯 RL 電路的交流情況

我們已經看到，流經純電感線圈的電流滯後電壓 90o，當我們說純電感線圈時，我們指的是沒有歐姆電阻的電感，因此沒有 I2 R 損耗。但在現實世界中，不可能只有純粹的交流電感。

所有電氣線圈、繼電器、螺線管和變壓器都將具有一定的電阻，無論與所使用的線圈匝數有多小。這是因為銅線具有電阻率。然後我們可以認為我們的感應線圈是一個由電阻 R 和 電感 L 串聯組成，成為一個可以被稱為“不純電感”的電感線圈。

如果線圈具有一些“內部”電阻，那麼我們需要將線圈的總阻抗表示為與電感串聯的電阻。在包含電感 L 和電阻 R 的交流電路中，RL 的組合電壓 V 是兩個分量電壓 VR 和 VL 的相量和。

這意味著流過線圈的電流仍將滯後於電壓，但是取決於 VR 和 VL 的值，相量之和小於 90o。電壓和電流波形之間的新角度給出了它們的相位差，正如我們所知，電路的相位角為 Φ。

考慮下面的電路是純無感電阻 R 與純電感 L 串聯。

串聯電阻 - 電感電路

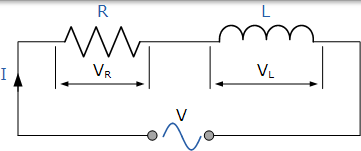
在上面的 RL 串聯電路中，我們可以看到電流對電阻和電感都是共同的，而電壓由兩個分量電壓 VR 和 VL 組成。可以通過數學方法或通過繪製向量圖找到這兩個分量的最終電壓。為了能夠產生向量圖，必須找到參考變數，因為在串聯 AC 電路中，相同的電流流過電阻和電感，所以電流是參考源。純電阻和純電感的單獨向量圖如下：

兩種純元件的向量圖

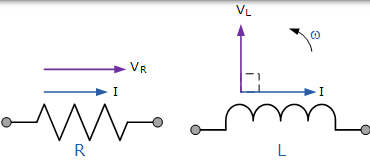
我們可以從上面和我們之前的關於交流電阻的教程中看到，電阻電路中的電壓和電流都是同相的，因此向量 VR 被疊加以繪製到電流向量上。此外，從上述可知，電流滯後於（純）交流電感電壓，因此向量 VL 畫在在電流前面 90o，長度為 V-R 的相同比例，如圖所示。

合成電壓的向量圖

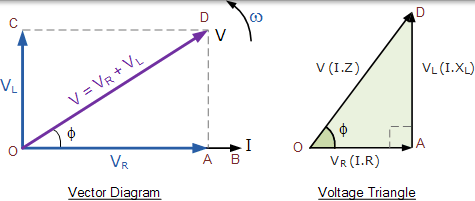
從上面的向量圖中，我們可以看到線 OB 是水平電流參考，線 OA 是電阻元件上與電流同相的電壓。線 OC 表示在電流前 90o 的感應電壓，因此仍然可以看出電流滯後純電感電壓 90o。線路 OD 為我們提供了最終的電源電壓。然後：

• V 等於施加電壓的有效值。
• I 等於串聯電流的有效值。
• VR 等於電阻上的 IR 電壓降，該電壓與電流同相。
• VL 等於電感兩端的 IXL 電壓降，它超前電流 90o。

由於純電感電流在正好滯後於電壓 90o， 從單獨的電壓得出的所得相量圖 VR 和 VL 代表如上所示的直角的三角形電壓 OAD。然後我們也可以使用畢達哥拉斯定理在數學上找到電阻/電感（RL）電路上的合成電壓值。

當 VR = IR 且 VL = IXL 時，所施加的電壓將是兩者的向量和，如下：

$$ \begin{array} { c } { \mathrm { V } ^ { 2 } = \mathrm { V } _ { \mathrm { R } } ^ { 2 } + \mathrm { V } _ { \mathrm { L } } ^ { 2 } } \\ { \mathrm { V } = \sqrt { \mathrm { V } _ { \mathrm { R } } ^ { 2 } + \mathrm { V } _ { \mathrm { L } } ^ { 2 } } } \\ { \mathrm { V } = \sqrt { ( \mathrm { IR } ) ^ { 2 } + \left( \mathrm { I } . \mathrm { X } _ { \mathrm { L } } \right) ^ { 2 } } } \\ { \therefore \mathrm { I } = \frac { \mathrm { V } } { \sqrt { \mathrm { R } ^ { 2 } + \mathrm { X } _ { \mathrm { L } } ^ { 2 } } } } \end{array} $$

$\sqrt { \mathrm { R } ^ { 2 } + \mathrm { X } _ { \mathrm { L } } ^ { 2 } }$ 表示電路的阻抗 Z。

交流電感的阻抗

阻抗 Z 是對包含電阻（實部）和電抗（虛部）的交流電路中流動的電流的“全部”抵抗。阻抗也以歐姆 ω 作為單位。阻抗取決於電路的頻率 ω，因為這會影響電路的無功元件，而在串聯電路中，所有的電阻和無功阻抗都會加在一起。

阻抗也可以用複數表示，Z = R + jXL， 但它不是相量，它是兩個或多個相量結合在一起的結果。如果我們將電壓三角形的邊上方除以 I，則得到另一個三角形，其邊代表電路的電阻，電抗和阻抗，如下所示。

RL 阻抗三角形

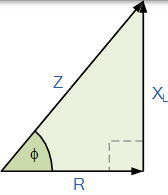
$$ \begin{array} { c } { Z = \frac { V } { I } } \\ { Z = \sqrt { R ^ { 2 } + X _ { L } ^ { 2 } } } \\ { \therefore Z ^ { 2 } = \left( R ^ { 2 } + X _ { L } ^ { 2 } \right) } \end{array} $$

阻抗2 = 電阻2 + （J 電抗)2， 其中 j 表示 90o 相移。

這意味著電壓和電流之間的正相角 θ 為。

相位角

$$ \begin{aligned} \mathrm { Z } ^ { 2 } & = \mathrm { R } ^ { 2 } + \mathrm { X } _ { \mathrm { L } } ^ { 2 } \\ \cos ^ { - 1 } \phi & = \frac { \mathrm { R } } { \mathrm { Z } } \\ \sin ^ { - 1 } \phi & = \frac { \mathrm { X } _ { \mathrm { L } } } { \mathrm { Z } } \\ \tan ^ { - 1 } \phi & = \frac { \mathrm { X } _ { \mathrm { L } } } { \mathrm { R } } \end{aligned} $$

雖然我們上面的例子代表了一個簡單的非純交流電感，但如果兩個或多個感應線圈串聯在一起，或者一個線圈與許多無感電阻串聯，那麼電阻元件的總電阻將相等至： R1 + R2 + R3 等，這樣求出電路的總電阻值。

同樣，電感元件的總電抗等於：X1 + X2 + X3 等，求出電路的總電抗值。這樣，包含許多扼流圈，線圈和電阻器的電路可以容易地求出單個阻抗值 Z，它由與等效的單個電阻串聯單個等效電感，Z2 = R2 + X2。

交流電感例項 No1

在下面的電路中，電源電壓定義為： V(t) = 230 sin(314t - 30o) ，L = 2.2H。確定流過線圈的電流值並繪製得到的相量圖。

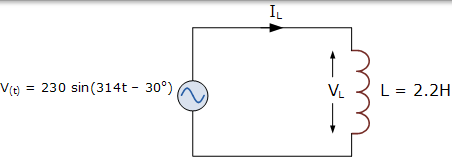
線圈兩端的電壓與電源電壓相同。將此時域值轉換為極座標形式可得出： VL = 230∠-30o V。線圈的感抗是： XL = ωL = 314×2.2 = 690 Ω。然後使用歐姆定律找到流過線圈的電流：

$$ \mathrm { I } _ { \mathrm { L } } = \frac { \mathrm { V } _ { \mathrm { L } } } { \mathrm { j } \mathrm { X } _ { \mathrm { L } } } = \frac { 230 \angle - 30 ^ { \circ } } { 690 } \angle 90 ^ { \circ } = 0.33 \angle 120 ^ { \circ } ( \mathrm { A } ) $$

結合電流滯後於電壓 90o， 相量圖如下，

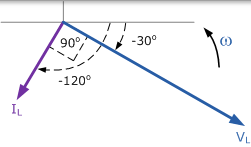
交流電感例項 No2

線圈的電阻為 30Ω，電感為 0.5H。如果流過線圈的電流是 4 安培，頻率為 50Hz，電源電壓的值是多少？

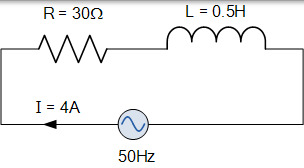
電路的阻抗將是：

$$ \begin{aligned} \mathrm { X } _ { \mathrm { L } } & = 2 \pi f \mathrm { L } = 2 \pi \times 50 \times 0.5 = 157 \Omega \\ \mathrm { Z } & = \sqrt { \mathrm { R } ^ { 2 } + \mathrm { X } _ { \mathrm { L } } ^ { 2 } } \\ \mathrm { Z } & = \sqrt { 30 ^ { 2 } + 157 ^ { 2 } } \\ \mathrm { Z } & = 159.8 \Omega \end{aligned} $$

然後，每個元件的電壓降計算如下：

$$ \begin{array} { l } { \mathrm { V } _ { \mathrm { S } } = \mathrm { I.Z } = 4 \times 159.8 = 640 \mathrm { v } } \\ { \mathrm { V } _ { \mathrm { R } } = \mathrm { I.R } = 4 \times 30 = 120 \mathrm { v } } \\ { \mathrm { V } _ { \mathrm { L } } = \mathrm { I.X } _ { \mathrm { L } } = 4 \times 157 = 628 \mathrm { v } } \end{array} $$

電流和電源電壓之間的相角計算如下：

$$ \tan ^ { - 1 } \phi = \frac { \mathrm { X } _ { \mathrm { L } } } { \mathrm { R } } = \frac { 157 } { 30 } = 79.2 ^ { \circ } $$

相量圖將是。

在下一個關於交流電容的教程中，我們將看一下電容器的穩壓狀態正弦交流波形的電壓 - 電流關係，以及純電容和非純電容的相量圖表示。