交流電容和電容電抗

電流通過交流電容的反對稱為電容電抗，其本身與供電頻率成反比

電容器以電荷的形式將能量儲存在其導電板上。當電容器連線在直流電源電壓上時，它以由其時間常數確定的速率充電到所施加電壓的值。

只要存在電源電壓，電容器將無限期地保持或保持該電荷。在該充電過程期間，充電電流 i 以與電壓在板上的電荷變化率相等的速率通過電壓的任何變化而流入電容器。因此，電容器與流到其板上的電流相反。

該充電電流與電容器供電電壓變化率之間的關係可在數學上定義為：i = C（dv / dt），其中 C 是電容器的電容值，單位為法拉，dv / dt 是電源電壓隨時間的變化。一旦它“完全充電”，電容器就會阻止任何更多電子流入其板上，因為它們已經飽和，電容器現在就像一個臨時儲存裝置。

即使去掉直流電源電壓，純電容器也會在其極板上無限期地保持這種電荷。然而，在包含“AC 電容”的正弦電壓電路中，電容器將以由電源頻率確定的速率交替地充電和放電。然後，交流電路中的電容器分別持續充電和放電。

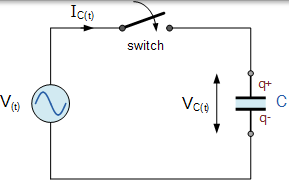
當交流正弦電壓施加到 AC 電容器的極板時，電容器首先在一個方向上充電，然後在相反方向上以與 AC 電源電壓相同的速率改變極性。電容器兩端的電壓瞬時變化與以下事實相反：將電荷沉積（或釋放）到板上需要一定的時間，並且由 V = Q / C 給出。考慮下面的電路。

具有正弦電源的交流電容

當開關在上述電路中閉合時，高電流將開始流入電容器，因為在 t = 0 時板上沒有電荷。正弦電源電壓 V 在其最大速率下以正方向增加，因為它在給定為 0o 的時刻穿過零參考軸。由於跨板的電位差的變化率現在處於其最大值，因此當最大電子量從一個板移動到另一個板時，流入電容器的電流也將處於其最大速率。

由於正弦電源電壓達到其 90o 上它開始減慢波形和在時間上非常簡短瞬間橫跨板的電位差被既不增加也不因此減小電流降低到零，因為沒有電壓的速率點更改。在這 90o 點電容器兩端的電位差是在其最大（ Vmax）時，沒有電流流入到電容器作為電容器現在已經完全充電，並且在其板用電子飽和的。

在該時刻結束時，電源電壓開始在負方向上向下朝向零參考線 180° 減小。雖然電源電壓本質上仍是正電壓，但電容器開始在其板上放電一些多餘的電子，以保持恆定的電壓。這導致電容器電流沿相反方向或負方向流動。

當電源電壓波形在瞬間 180° 穿過零參考軸點時，正弦電源電壓的變化率或斜率處於其最大值但處於負方向，因此流入電容器的電流也處於其最大速率。那個瞬間。此外，在此 180o 點橫跨板的電勢差是零電荷的量相等的兩個板之間分配。

然後在這個第一半週期 0o 到 180o 的電流達到它的最大正值，換句話說，施加到一個純電容電路的電壓之後施加的電壓達到其最大正值的週期的四分之一（1 /4ƒ） “滯後”，由一個週期的四分之一或 90 的當前直徑： 如下所示。

交流電容的正弦波形

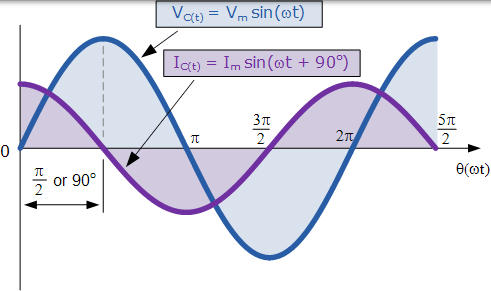
在 180° 至 360°的後 半週期期間，電源電壓反轉方向並朝 270°的 負峰值前進。此時，板上的電位差既不減小也不增加，電流減小到零。電容器兩端的電位差是在其最大的負值時，沒有電流流入到電容器和它變成完全充電一樣在其 90o 點，但在相反的方向。

當負電源電壓開始朝零基準線上的 360° 點正方向增加時，完全充電的電容器現在必須鬆開一些多餘的電子，以保持與之前一樣的恆定電壓並開始自我放電，直到供電電壓在 360° 達到零，充電和放電過程再次開始。

根據上面的電壓和電流波形和描述，我們可以看到電流總是將電壓超前一個週期的 1/4 或 π/ 2 = 90o “異相”與電容器之間的電位差，因為這個充電和放電過程。然後，交流電容電路中的電壓和電流之間的相位關係與我們在前一個教程中看到的交流電感完全相反。

這種效應也可以用相量圖表示，其中在純電容電路中電壓 LAGS 電流為 90o。但是，通過使用該電壓作為我們的參考，我們也可以說，目前的由週期的四分之一或 90 LEADS 電壓o 如示於下面的向量圖。

交流電容的相量圖

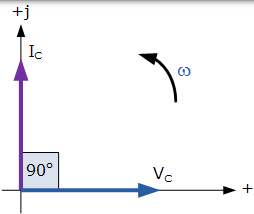
因此，對於一個純電容，VC “滯後” IC 90o，或者我們可以說，IC 超前 VC 90o。

有許多不同的方法可以記住純交流電容電路中流過的電壓和電流之間的相位關係，但一種非常簡單易記的方法是使用稱為 ICE 的助記符表示式。ICE 代表電流 I 首先在交流電容 C 中，在 E 電動勢之前。換句話說，電容器中的電壓之前的電流，I，C，E 等於 ICE ，無論電壓從哪個相角開始，這個表示式總是適用於純交流電容電路。

電容電抗

因此，我們現在知道電容器對抗電壓的變化，電容器上的電子流與電容器充電和放電時電路板上的電壓變化率成正比。與電阻相反的電阻不同於電阻，電容中電流的反對稱為電抗。

與電阻一樣，電抗以歐姆為單位測量，但是給出符號 X 以區別於純電阻 R 值，並且因為所討論的元件是電容器，電容器的電抗稱為電容電抗，（ XC）測量在歐姆。

由於電容器的充電和放電與它們之間的電壓變化速率成比例，電壓變化越快，電流將越多。同樣，電壓變化越慢，流動的電流越小。這意味著交流電容器的電抗與電源頻率“成反比”，如圖所示。

電容電抗

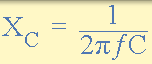
其中： XC 是容抗在歐姆， ƒ 是頻率（赫茲）和 C 單位是法拉的電容 AC，符號 F。

在處理交流電容時，我們也可以用弧度來定義容抗，其中歐米茄， ω 等於 2π。

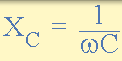
從上面的公式我們可以看出，隨著頻率的增加，電容電抗的值及其整體阻抗（以歐姆為單位）減小到零，就像短路一樣。同樣地，當頻率接近零或 DC 時，電容器電抗增加到無窮大，起到開路的作用，這就是電容器阻斷 DC 的原因。

容性電抗和頻率之間的關係與我們在前一個教程中看到的感應電抗（ XL） 完全相反。這意味著容性電抗“與頻率成反比”並且在低頻處具有高值而在較高頻率處具有低值，如圖所示。

對頻率的電容反應

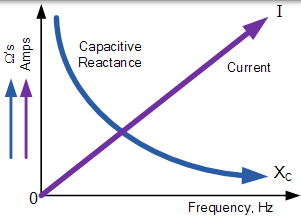
電容器的電容電抗隨著其板上的頻率增加而降低。因此，容抗與頻率成反比。電容電抗對抗電流，但板上的靜電電荷（其交流電容值）保持不變。

這意味著電容器在每個半週期期間更容易完全吸收其板上的電荷變化。此外，隨著頻率增加，流入電容器的電流值增加，因為其板上的電壓變化率增加。

我們可以將非常低和非常高的頻率對純 AC 電容的電抗的影響表示如下：

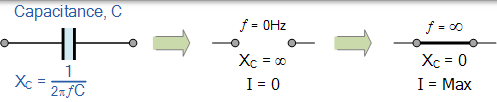
在包含純電容的交流電路中，流入電容器的電流（電子流）如下：

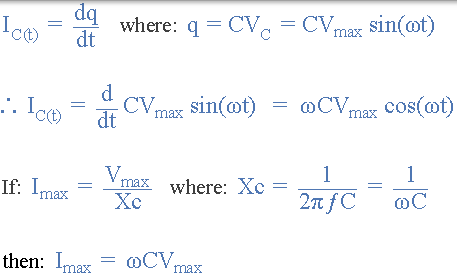
因此，流入交流電容的均方根電流定義為：

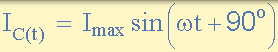
其中： IC = V /（1 /ωC） （或 IC = V / XC）是電流幅度， θ= + 90o 是電壓和電流之間的相位差或相位角。對於純電容電路，Ic 使 Vc 超過 90o，或者 Vc 超過 Ic 90o。

相量域

在相量域中，交流電容板上的電壓將為：

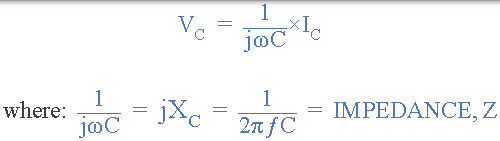
在極座標形式，這將被寫為： XC ∠-90o 其中：

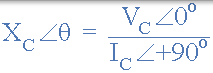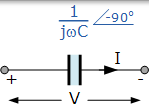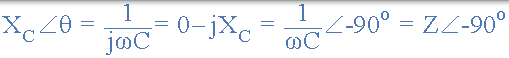
串聯 R + C 電路的交流電

我們從上面看到，流入純交流電容的電流導致電壓達到 90o。但在現實世界中，不可能有純**交流電容，**因為所有電容器在其板上都會有一定量的內阻，從而產生漏電流。

然後我們可以認為我們的電容器是具有電阻的電容器，R 與電容串聯，C 產生可以被稱為“不純電容器”的電容器。

如果電容器具有一些“內部”電阻，那麼我們需要將電容器的總阻抗表示為與電容串聯的電阻，並且在包含電容，C 和電阻的交流電路中，R 表示電壓相量，V，組合將等於兩個分量電壓 VR 和 VC 的相量和。

這意味著然後使流入電容器的電流仍然會導致的電壓，而是通過的量小於 90o 取決於的值 [R 和 C ^ 給我們用希臘符號披給出它們之間的相應的相位角的相量和， Φ。

考慮下面的串聯 RC 電路，其中歐姆電阻 R 與純電容 C 串聯連線。

串聯電阻電容電路

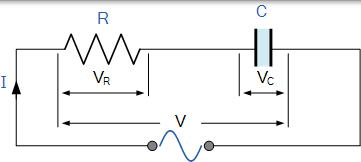
在上面的 RC 串聯電路中，我們可以看到流入電路的電流對電阻和電容都是共同的，而電壓則由兩個分量電壓 VR 和 VC 組成。將得到的這兩種組分的電壓可以在數學上找到但是由於向量 VR 和 VC 90o 出異相，可以將它們向量通過構建的向量圖加入。

為了能夠產生 AC 電容的向量圖，必須找到參考或公共部件。在串聯 AC 電路中，電流是常見的，因此可以用作參考源，因為相同的電流流過電阻並流入電容。純電阻和純電容的單獨向量圖如下：

兩種純組分的向量圖

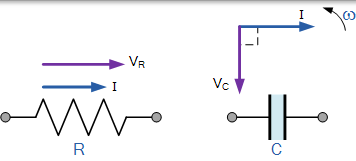
交流電阻的電壓和電流向量都彼此同相，因此電壓向量 VR 被疊加以按比例繪製到電流向量上。此外，我們知道，目前導致在純 AC 電容電路中的電壓（ICE），因此電壓向量 Vc ^ 被拉 90o 後面（滯後）的電流向量和相同比例為 VR，如圖所示。

向量圖的結果電壓

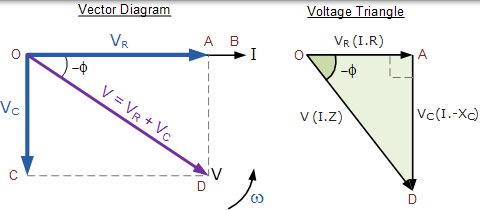
在上面的向量圖中，線 OB 表示水平電流參考，線 OA 是電阻元件兩端的電壓，其與電流同相。線 OC 示出了電容式電壓，該電壓 90o 當前因此它仍然可以看出，目前由 90 導致的純電容電壓後面o。線路 OD 為我們提供了最終的電源電壓。

由於電流超前於電壓在 90 純電容o 從各個電壓繪製的所得相量圖滴 VR 和 VC ^ 代表如上示出為直角的三角形電壓 OAD。然後我們也可以使用畢達哥拉斯定理在數學上找到電阻/電容（RC）電路上的合成電壓值。

當 VR = IR 且 VC = IXC 時，所施加的電壓將是兩者的向量和，如下所示。

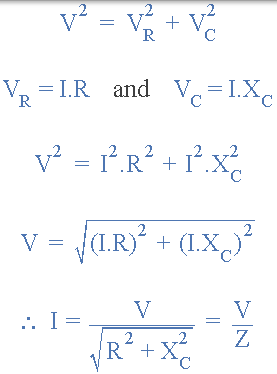
量表示阻抗， Z 電路。 ****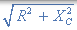

交流電容的阻抗

阻抗，Z 具有歐姆單位， ω 是對包含電阻（實部）和電抗（虛部）的交流電路中流動的電流的“全部”反對。純電阻阻抗將具有 0 的相位角o 而純電容性阻抗將具有-90 的相位角o。

然而，當電阻器和電容器在同一電路中被連線在一起時，總阻抗將具有相位角 0 的地方之間o 和 90o 取決於所使用的成分的值。然後通過使用阻抗三角形可以找到上面所示的簡單 RC 電路的阻抗。

RC 阻抗三角形

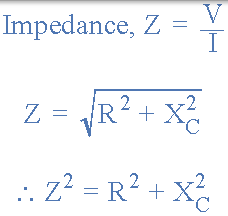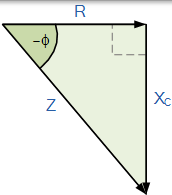然後： （阻抗）2 =（電阻）2 +（J 電抗）2 其中 J 表示 90o 相移。

這意味著通過使用畢達哥拉斯定理，負相角，電壓和電流之間的 θ 計算為。

相位角

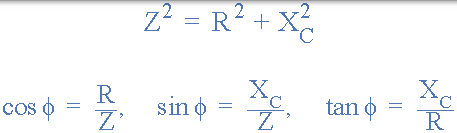
交流電容示例 No1

定義為： V(t) = 240 sin（314t - 20o） 的單相正弦交流電源電壓連線到 200uF 的純交流電容。確定流入電容器的電流值並繪製得到的相量圖。

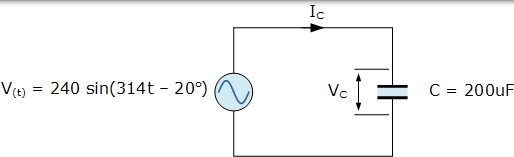
電容兩端的電壓與電源電壓相同。將此時域值轉換為極座標形式可得出： VC =240∠-20o （v） 。容抗將為： XC = 1 /（ω.200uF） 。然後使用歐姆定律可以找到流入電容器的電流：

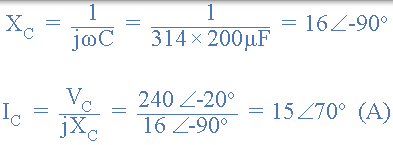
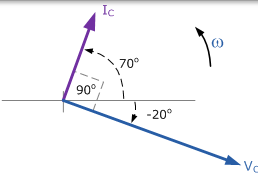
與當前主導 90 的電壓o 在 AC 電容電路的相量圖會。

交流電容示例 No2

內部電阻為 10Ω，電容值為 100uF 的電容器連線到 V(t) = 100sin(314t) 的電源電壓。計算流入電容器的電流。還構造一個電壓三角形，顯示各個電壓降。

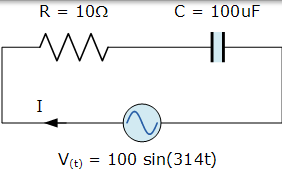
容抗和電路阻抗計算如下：

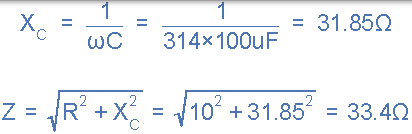
然後流入電容器和電路的電流如下：

電流和電壓之間的相位角由上面的阻抗三角形計算得出：

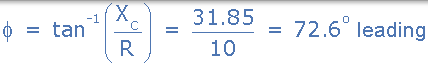
然後，電路周圍的各個電壓降計算如下：

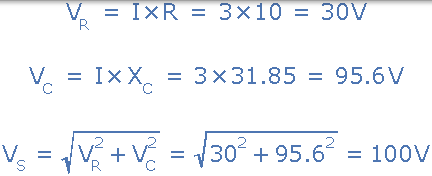
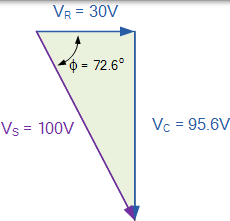
然後，計算出的峰值的合成電壓三角形將為：

交流電容總結

在純 AC 電容電路中，電壓和電流都為“外的相”與當前由 90 超前於電壓o，我們可以通過使用助記符表達記住這個 ICE 。電容器稱為阻抗的 AC 電阻值，（Z）是與頻率與所謂的“電容性電抗”電容器，的反應性值 XC。在 AC 電容電路中，該容抗電阻值等於 1 /（2πC） 或 1 /（jωC）

到目前為止，我們已經看到電壓和電流之間的關係並不相同，並且所有三個純無源元件都發生了變化。在電阻相位角為 0o，在電感是 90o 而在電容它是-90o。

在下一個關於 RLC 系列電路的教程中，當應用穩態正弦交流波形以及相應的相量圖表示時，我們將在相同的串聯電路中連線在一起時，檢視所有這三個無源元件的電壓 - 電流關係。