平均電壓教程

在本教程中,我們將使用中座標規則和分析規則來計算正弦波形的“平均”或平均電壓值。
用於找到交流波形的平均電壓的過程非常類似於找到其 RMS 值的過程,此時的差異是瞬時值不是平方的,並且我們沒有找到求和平均值的平方根。
無論是正弦波,方波還是三角波,週期波形的平均電壓(或電流)定義為:“波形下面積相對於時間的商”。換句話說,沿時間軸對所有瞬時值進行平均,其中時間為一個完整週期( T)。
對於週期性波形,水平軸上方的區域為正,而水平軸下方的區域為負。結果是對稱交變數的平均值或平均值因此為零,(0)因為水平軸上方的區域(正半週期)與軸下方的區域(負半週期)相同,並且從而相互抵消。這是因為當我們對兩個區域進行數學運算時,負區域會抵消產生零平均電壓的正區域。
那麼對稱交變數的平均值或平均值,例如正弦波,是僅在一個週期的一半上測量的平均值,因為正如我們剛才所說的,一個完整週期的平均值為零,而不管峰值幅度。
電氣術語平均電壓和平均電壓或甚至平均電流可用於交流和直流電路分析或計算。用於表示平均值的符號定義為: VAV 或 IAV。
平均電壓圖形方法
再次考慮前一個 RMS 電壓教程的正半週期。通過採用等間隔的瞬時值,可以以合理的精度再次找到波形的平均電壓或平均電壓。
波形的正半部分被分成任意數量的 n 相等部分或中間縱座標。因此各中縱座標的寬度將 Ño 度(或t秒),並且每個中間縱座標的高度將等於波形的在沿著波形的 x 軸該點處的瞬時值。
圖形方法
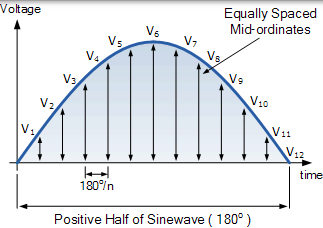
電壓波形的每個中間值加到下一個,總和,V1 到 V12 除以用於給出平均電壓 的中間數。然後平均電壓( VAV)是電壓波形的中間座標的平均值,並給出如下:

因此,對於上面的簡單示例,平均電壓計算如下:

因此,如前所述,我們再次假設 20 伏峰值的交流電壓在半個週期內變化如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 電壓 | 6.2V | 11.8V | 16.2V | 19.0V | 20.0V | 19.0V | 16.2V | 11.8V | 6.2V | 0V |
| 角度 | 18o | 36o | 54o | 72o | 90o | 108o | 126o | 144o | 162o | 180o |
因此,平均電壓值計算如下:
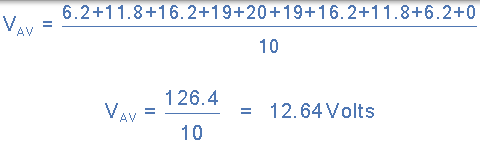
然後使用圖形方法的半個週期的平均電壓值給出為: 12.64 伏特。
平均電壓分析方法
如前所述,兩個半部完全相似的週期性波形的平均電壓,無論是正弦波還是非正弦波,在一個完整週期內將為零。然後,通過僅在一個半週期上加上電壓的瞬時值來獲得平均值。但是在非對稱或複雜波的情況下,必須在數學上在整個週期迴圈中取平均電壓(或電流)。
平均值可以通過將曲線下面積以不同的間隔近似於基底的距離或長度來數學地取得,這可以使用如圖所示的三角形或矩形來完成。
區域的近似
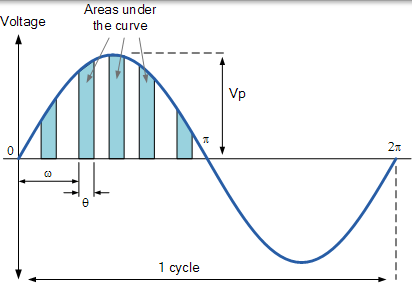
通過近似曲線下方矩形的區域,我們可以粗略地瞭解每個區域的實際面積。通過將所有這些區域加在一起,可以找到平均值。如果使用無限數量的較小的較薄矩形,則當它接近 2 /π 時,最終結果將更準確。
曲線下面積可以通過各種近似方法找到,例如梯形法則,中座標法則或辛普森法則。然後,在週期波的正半週期下的數學區域被定義為 V(t) = Vp.cos(ωt) ,其週期為 T,使用積分如下:

其中:0 和 π 是積分的極限,因為我們確定電壓超過半個週期的平均值。然後在曲線下方的區域最終被給定為面積= 2VP。由於我們現在知道正半週期(或負半週期)下的面積,我們可以通過在半個週期內積分正弦量併除以週期的一半來輕鬆確定正弦波形的正(或負)區域的平均值。。
例如,如果正弦波的瞬時電壓給定為: v =Vp.sinθ,並且正弦波的週期給定為: 2π,則:
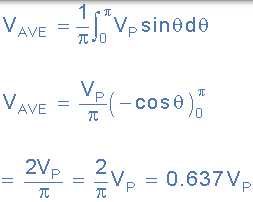
因此,作為正弦波平均電壓的標準公式給出:
平均電壓方程

通過將峰值電壓值乘以常數 0.637 來確定正弦波形的平均電壓( VAV),常數 0.637 除以 pi( π)。平均電壓(也可以稱為平均值)取決於波形的大小,並且不是頻率或相位角的函式。
因此,正弦波形的該平均值或平均值(電壓或電流)也可以表示為面積和時間的等效 DC 值。

在一個完整週期內平均值為零,因為正平均面積將被兩個區域之和的負平均面積(VAVG - (- VAVG)) 抵消,從而導致一個完整的平均電壓為零正弦波的迴圈。
參考上面的圖形示例,峰值電壓( Vpk)為 20 伏特。因此,使用分析方法,平均電壓計算如下:
VAV = Vpk x 0.637 = 20×0.637 = 12.74 伏
這與圖形方法的值相同。
要從給定的平均電壓值中找到峰值,只需重新排列公式併除以常數。例如,如果平均值是 65 伏,那麼正弦峰值 Vpk 是多少。
Vpk = VAV ÷0.637 = 65÷0.637 = 102 伏
請注意,將峰值或最大值乘以常數 0.637 僅適用於正弦波形。
平均電壓彙總
然後總結一下。當處理交流電壓(或電流)時,術語平均值通常取一個完整週期,而術語平均值用於週期週期的一半。
在一個完整週期內整個正弦波形的平均值為零,因為兩個半部相互抵消,因此平均值取半個週期。電壓或電流的正弦波的平均值是峰值的 0.637 倍( Vp 或 Ip。平均值之間的這種數學關係適用於 AC 電流和 AC 電壓。
有時需要能夠計算整流器或脈衝型電路(例如 PWM 電動機電路)的直流電壓或電流輸出值,因為電壓或電流雖然沒有反轉,但卻在不斷變化。由於沒有相位反轉,因此使用平均值,並且 RMS(均方根)值對於此類應用而言並不重要。
RMS 電壓和平均電壓之間的主要差異在於,週期波的平均值是在波形的給定週期內在曲線下采集的所有瞬時面積的平均值,並且在正弦量的情況下,這段時間被視為波浪週期的*一半。為方便起見,通常使用正半週期。
波形的有效值或均方根(RMS)值是波的有效熱值與穩定的直流值相比,是在一個完整週期內取得的瞬時值的平方平均值的平方根。
僅對於純正弦波形,平均電壓和 RMS 電壓(或電流)可以很容易地計算為:
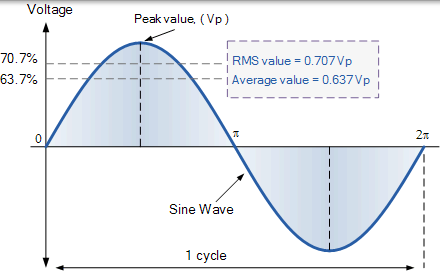
平均值 = 0.637×最大值或峰值 Vpk
RMS 值 = 0.707×最大值或峰值 Vpk
關於使用平均電壓和** RMS 電壓的**最後評論。兩個值都可用於表示正弦交流波形的“形狀因子”。形狀因子被定義為 AC 波形的形狀,並且是 RMS 電壓除以平均電壓(形狀因子= rms 值/平均值)。
因此,對於正弦或複雜的波形的形狀因數被給定為:( π/(2√ 2) ),其是近似等於恆定,1.11。形狀因子是比率,因此沒有電氣單位。如果已知正弦波形的形狀因子,則可以使用 RMS 電壓值找到平均電壓,反之亦然,因為平均電壓是正弦波的 RMS 電壓值的 0.9 倍。