无源高通滤波器

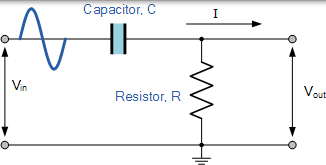
高通滤波器与低通滤波器电路完全相反，因为两个元件已经互换，滤波器输出信号现在从电阻器中得到。

其中作为低通滤波器只允许低于其截止频率 ƒc 的信号通过，无源高通滤波器电路正如其名称所暗示的，仅通过所选择的分界点 ƒc 以上的信号，从而滤除了任何低频信号波形。考虑下面的电路。

高通滤波器电路

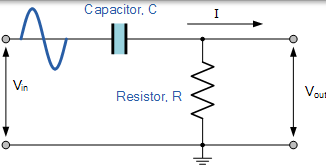
在这种电路中，电容器的电抗在低频时非常高，因此电容器的作用类似于开路，并且在 VIN 处阻止任何输入信号，直到达到截止频率点 fC。在该截止频率点以上，电容器的电抗已经充分降低，现在更像是短路，允许所有输入信号直接传递到输出，如下面滤波器响应曲线所示。

一阶高通滤波器的频率响应

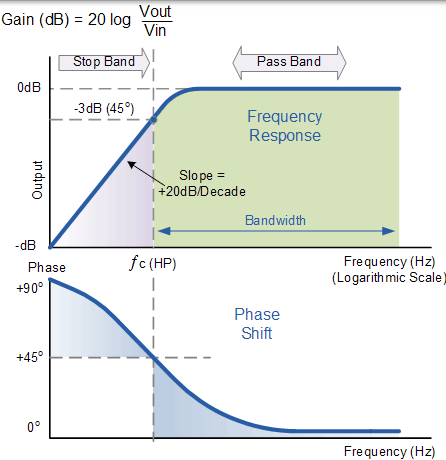
上面的无源高通滤波器的波特图或频率响应曲线与低通滤波器的波特图或频率响应曲线完全相反。这里信号在低频衰减，输出以 +20dB / Decade（6dB / Octave）的斜率上升，直到频率达到截止点（ ƒc ），这里 R = Xc。它的响应从无限低延申至截止频率，其中输出电压幅度是输入信号值的 1 /√2 = 70.7% 的或输入的 -3dB（20 log (Vout/Vin)）。

此外，我们可以看出，输出信号的相位角 Φ 超前 输入，在频率 ƒc 处等于 45o。此滤波器的频率响应曲线意味着滤波器可以将传递到直无穷大的所有信号。然而，在实际中，滤波器响应不会延伸到无穷大，而是受所用元件的电气特性的限制。

可以使用与低通滤波器相同的等式找到一阶高通滤波器的截止频率点，但是相移的公式稍微修改了下，以适应正相移的情况，如下所示。

截止频率和相移

$$ \begin{array} { l } { f c = \frac { 1 } { 2 \pi R C } } \\ { \text { Phase Shift } \phi = \arctan \frac { 1 } { 2 \pi f R C } } \end{array} $$

电路增益 Av 以 Vout / Vin（幅度）给出，计算公式如下：

$$ A _ { v } = \frac { V _ { O U T } } { V _ { I N } } = \frac { R } { \sqrt { R ^ { 2 } + X c ^ { 2 } } } = \frac { R } { Z } $$

在低频处，$\mathrm { Xc } \rightarrow \infty , ) Vout ( = 0$

在高频处，$\mathrm { Xc } \rightarrow 0 , ) Vout ( = \mathrm { Vin }$

高通滤波器示例 No1

计算一个简单的无源高通滤波器的截止频率 ƒc，该滤波器由一个与 240kΩ 电阻串联的 82pF 电容组成。

$$ f c = \frac { 1 } { 2 \pi R C } = \frac { 1 } { 2 \pi \times 240,000 \times 82 \times 10 ^ { - 12 } } = 8,087 H z \text { or } 8 k H z $$

二阶高通滤波器

与低通滤波器一样，高通滤波器级可以级联在一起以形成如图所示的二阶（两极）滤波器。

二阶高通滤波器

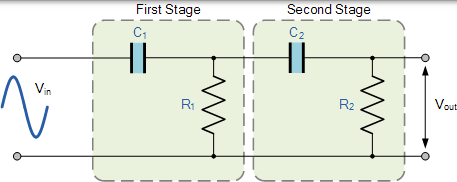
上述电路使用两个一阶滤波器连接或级联在一起形成二阶或两极高通网络。然后，通过简单地使用额外的 RC 网络，可以将一阶滤波器级转换为二阶类型，与二 阶低通滤波器的道理相同。得到的二阶高通滤波器电路的斜率为 40dB / decade（12dB /octave）。

与低通滤波器一样，截止频率 ƒc 由电阻器和电容器决定，如下所示。

$$ f _ { \mathrm { C } } = \frac { 1 } { 2 \pi \sqrt { \mathrm { R } _ { 1 } \mathrm { C } _ { 1 } \mathrm { R } _ { 2 } \mathrm { C } _ { 2 } } } \mathrm { Hz } $$

高通滤波器摘要

我们已经看到无源高通滤波器与低通滤波器完全相反。该滤波器没有 DC(0Hz) 的输出电压，直到指定的截止频率 ƒc 点。截止频率点是允许通过的电压增益的 70.7% 或 -3dB （dB = -20log VOUT / VIN ）。

截止点 ƒc 以下的频率范围通常称为阻带，而“高于”该截止点的频率范围通常称为通带。

使用标准公式： ƒc= 1 /(2πRC) 可以找到高通滤波器的截止频率，转角频率或 -3dB 点。在所得到的输出信号的相位角 ƒc 是 45o。通常，由于较高的工作频率，高通滤波器比其等效低通滤波器的失真更小。

这种类型的无源滤波器的一个非常常见的应用是在音频放大器中作为两个音频放大器级之间的耦合电容器和扬声器系统，以将较高频率的信号引导到较小的“高音扬声器”型扬声器，同时阻挡较低的低音信号或者是也用作滤波器以减少任何低频噪声或“隆隆”型失真。当在音频应用中这样使用时，高通滤波器有时被称为“低切”或“低音切割”滤波器。

如前所述，输出电压 Vout 取决于时间常数和输入信号的频率。将 AC 正弦信号应用于电路时，它表现为简单的一阶高通滤波器。但是，如果我们将输入信号改变为具有几乎垂直阶跃输入的“方波”形信号，则电路的响应会发生显着变化并产生通常称为微分器的电路。

RC 微分器

到目前为止，滤波器的输入波形被假定为正弦波或由基波信号和在频域中工作的一些谐波组成的正弦波的输入波形，给出了滤波器的频域响应。但是，如果我们使用在时域中工作的方波信号为高通滤波器提供脉冲或阶跃响应输入，则输出波形将由短持续时间脉冲或尖峰组成，如图所示。

RC 微分电路

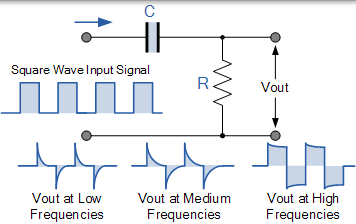
方波输入波形的每个周期在输出端产生两个尖峰，一个正极和一个负极，其幅度等于输入的幅度。尖峰的衰减速率取决于两个分量的时间常数 RC 值 (t = RC) 和输入频率的值。随着频率的增加，输出脉冲越来越像输入信号的形状。