电容电抗
电容电抗是电容器的复阻抗,其值随应用频率而变化.
在 RC 网络教程中,我们看到当直流电压施加到电容器时,电容器本身从电源吸取充电电流并充电至等于所施加电压的值。
同样,当电源电压降低时,存储在电容器中的电荷也会减少并且电容器放电。但是在交流电路中,所施加的电压信号以由电源频率确定的速率连续地从正极变为负极,例如正弦波电压的情况,电容器正在或以供应频率确定的速率连续充电或放电。
当电容器充电或放电时,电流流过电容器,电流受到电容器内部阻抗的限制。这种内部阻抗通常称为**电容电抗,**并以欧姆符号 XC 表示。
与具有固定值的电阻不同,例如,100Ω,1kΩ,10kΩ 等(这是因为电阻符合欧姆定律),电容电抗随施加的频率而变化,因此电源频率的任何变化都会对电容的容抗值产生很大影响。
随着施加到电容器的频率增加,其效果是降低其电抗(以欧姆为单位测量)。同样,当电容器两端的频率降低时,其电抗值也会增加。这种变化称为电容器的复阻抗。
存在复阻抗是因为电容器板上的电荷形式的电子看起来相对于变化的频率更快地从一个板传递到另一个板。
随着频率的增加,电容器在给定时间内在板上传递更多电荷,导致更大的电流流过电容器,就像电容器的内部阻抗减小一样。因此,连接到在给定频率范围内变化的电路的电容器可以说是频率相关的。
电容式电抗具有电气符号 XC,其单位为欧姆,与电阻(R)相同。它使用以下公式计算:
电容电抗
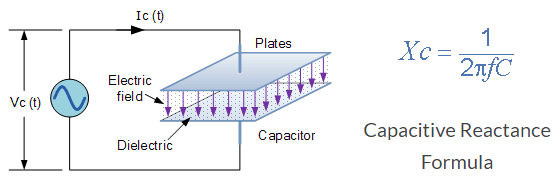
其中,
- Xc = 以欧姆表示的电容电抗(Ω)
- π = 3.142
- ƒ =以赫兹为单位的频率(Hz)
- C = 以法拉为单位的电容(F)
电容电抗实例 No1
计算频率为1kHz的220nF电容的容性电抗值,并再次计算频率为20kHz的容抗值。
- 频率为 1kHz:
$$ X c = \frac { 1 } { 2 \pi f C } = \frac { 1 } { 2 \pi \times 1000 \times 220 \times 10 ^ { - 9 } } = 723.4 \Omega $$
- 频率为 20kHz:
$$ X c = \frac { 1 } { 2 \pi f C } = \frac { 1 } { 2 \pi \times 20000 \times 220 \times 10 ^ { - 9 } } = 36.2 \Omega $$
其中:ƒ = 频率,C = 电容值
因此,从上面可以看出,当施加在 220nF 电容上的频率从 1kHz 增加到 20kHz 时,其电抗值 XC 从大约723Ω减小到仅36Ω,这总是正确的,因为容抗,XC 是与频率成反比,对于给定电压下,电容通过的电流与频率成比例。
对于任何给定的电容值,电容器的电抗,以欧姆表示的 XC 可以相对于频率绘制,如下所示。
电容电抗 vs 频率
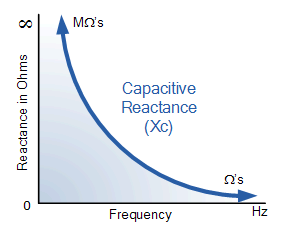
通过重新安排上述电抗公式,我们还可以找出电容器具有特定容性电抗 XC 值的频率 。
电容电抗实例 No2
2.2uF 电容在哪个频率下的电抗值为 200Ω?
$$ f = \frac { 1 } { 2 \pi C X c } = \frac { 1 } { 2 \pi \times 2.2 \times 10 ^ { - 6 } \times 200 } = 361.7 H z $$
或者我们可以通过了解该频率下的应用频率及其电抗值来找到电容的值。
电容电抗实例 No3
当电容电抗为 200Ω 且连接到 50Hz 电源时,电容的平均值是多少。
$$ C = \frac { 1 } { 2 \pi f X c } = \frac { 1 } { 2 \pi x 50 \times 200 } = 15.92 u F $$
从上面的例子我们可以看出,当连接到可变频率电源时,电容器有点像频率控制可变电阻器,因为它的电抗(X)与频率成正比。在非常低的频率,例如1Hz,我们的220nF电容器具有大约723.3KΩ的高容抗电抗值(产生开路效应)。
在诸如 1MHz 的非常高的频率下,电容器具有仅有 0.72Ω 的低容抗电阻值(产生短路效应)。因此,在零频率或稳态 DC 时,我们的220nF电容器具有无限电抗,看起来更像是板之间的开路,能阻挡任何通过它的电流。
分压器修订版
我们从关于串联电阻器的教程中记得,根据电阻值,每个电阻器上会出现不同的电压,并且分压器电路能够按照 R2 /(R1 + R2)的比率将电源电压分压。因此,当 R1 = R2 时,输出电压将是输入电压值的一半。同样,任何大于或小于 R1 的 R2 值都会导致输出电压成比例变化。考虑下面的电路。
分压网络
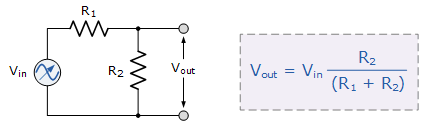
我们现在知道电容器的电抗 XC(其复阻抗)值相对于所施加的频率而变化。如果我们现在将电阻器 R2 变为电容器,则两个元件上的电压降会随着频率的变化而变化,因为电容器的电抗会影响其阻抗。
电阻器 R1 的阻抗不随频率变化。电阻器具有固定值,不受频率变化的影响。然后,电阻器R1两端的电压和输出电压由电容器在给定频率下的容抗决定。然后,这导致频率相关的RC分压器电路。考虑到这一点,可以通过用合适的电容替换其中一个分压电阻来构建无源低通滤波器和高通滤波器,如图所示。
低通滤波器
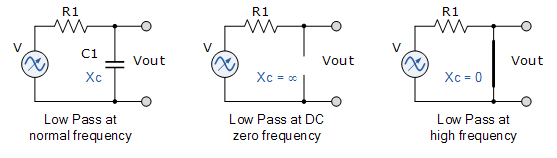
高通滤波器
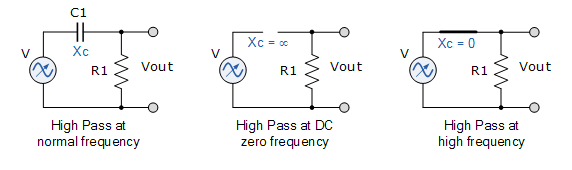
电容电抗的特性使电容器非常适用于交流滤波器电路或直流电源平滑电路,以减少任何不需要的纹波电压的影响,因为电容器在输出端子上施加短路信号路径到任何不需要的频率信号。
电容电抗总结
因此,我们可以将变频电路中电容器的行为概括为一种频率控制电阻器,该电阻器在极低频率下具有高容抗电阻值(开路条件),在非常高的频率下具有低容性电抗值(短路条件),如上图所示。
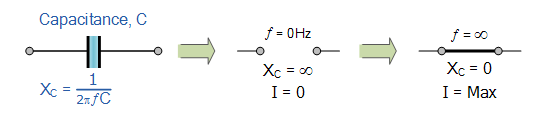
重要的是要记住这两个条件,在下一个关于无源低通滤波器的教程中,我们将研究使用电容电抗来阻止任何不需要的高频信号,同时只允许低频信号通过。