有源低通滤波器

通过将基本的 RC 低通滤波器电路与运算放大器相结合,我们可以创建一个有放大的有源低通滤波器电路
在 RC 无源滤波器教程中,我们看到了基本的一阶滤波器电路,如低通滤波器和高通滤波器,只需使用一个串联的电阻器与一个连接在正弦输入信号上的非极化电容器即可制成。
我们还注意到无源滤波器的主要缺点是输出信号的幅度小于输入信号的幅度,即增益绝不大于 1,并且负载阻抗会影响滤波器特性。
对于包含多级的无源滤波器电路,信号的衰减幅度损失会变得非常严重。恢复或控制信号损失的一种方法是通过使用有源滤波器进行放大。
顾名思义,有源滤波器在其电路设计中包含有源元件,如运算放大器、晶体管或 FET。它们从外部电源获取电源,并使用它来增强或放大输出信号。
滤波器放大还可用于通过产生更具选择性的输出响应来对滤波器电路的频率响应进行整形或改变,从而使滤波器的输出带宽更窄或更宽。那么无源滤波器和有源滤波器之间的主要区别在于增益是否放大。
有源滤波器通常在其设计中使用运算放大器(op-amp),在运算放大器教程中,我们看到运算放大器具有高输入阻抗,低输出阻抗和由其内部的反馈回路的电阻网络确定的电压增益。
与理论上具有无限高频响应的无源高通滤波器不同,有源滤波器的最大频率响应限于所使用的运算放大器的增益/带宽乘积(或开环增益)。尽管如此,有源滤波器通常比无源滤波器更容易设计,当使用良好的电路设计时,它们具有良好的性能特性,非常好的精度,陡峭的滚降和低噪声。
有源低通滤波器
最常见且易于理解的有源滤波器是有源低通滤波器。其工作原理和频率响应与之前看到的无源滤波器完全相同,这次唯一的区别是它使用运算放大器进行放大和增益控制。最简单形式的低通有源滤波器是将反相或非反相放大器(如运算放大器教程中讨论的相同)连接到基本 RC 低通滤波器电路,如图所示。
一阶低通滤波器
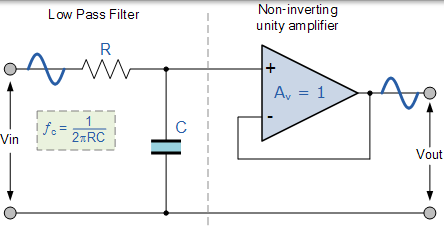
该一阶低通有源滤波器仅由无源 RC 滤波器级组成,为非反相运算放大器的输入提供低频路径。放大器配置为电压跟随器(缓冲器),其 DC 增益为 1,Av = +1 或单位增益,而不是之前的无源 RC 滤波器,其 DC 增益小于 1。
这种配置的优点是运算放大器的高输入阻抗可防止滤波器输出上的过载,同时其低输出阻抗可防止滤波器截止频率点受负载阻抗变化的影响。
虽然这种配置为滤波器提供了良好的稳定性,但其主要缺点是它没有高于 1 的电压增益。然而,虽然电压增益是单位,但功率增益非常高,因为其输出阻抗远低于其输入阻抗。如果需要大于 1 的电压增益,我们可以使用以下滤波器电路。
具有放大功能的有源低通滤波器
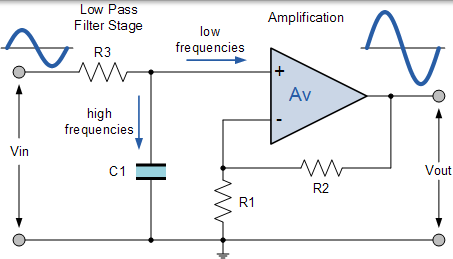
除了放大器的通带增益 AF 增加输出幅度外,电路的频率响应与无源 RC 滤波器的频率响应相同。对于非反相放大器电路,滤波器的电压增益幅度等于反馈电阻( R2 )除以其相应的输入电阻( R1 ),如下所示:
$$ \mathrm { DC } \text { gain } = \left( 1 + \frac { \mathrm { R } _ { 2 } } { \mathrm { R } _ { 1 } } \right) $$
因此,作为频率函数的有源低通滤波器的增益将是:
一阶低通滤波器的增益
$$ \text { Voltage Gain, } ( A v ) = \frac { \text {Vout} } { V i n } = \frac { A _ { F } } { \sqrt { 1 + \left( \frac { f } { f c } \right) ^ { 2 } } } $$
其中,
- AF =滤波器的通带增益( 1 + R2 / R1 )
- ƒ = 输入信号的频率,单位为赫兹(Hz)
- ƒc =以赫兹为单位的截止频率(Hz)
因此,可以从上面的频率增益公式验证低通有源滤波器的操作:
- 在非常低的频率下,ƒ<ƒc 时, $\frac { \mathrm { Vout } } { \mathrm { Vin } } \cong \mathrm { A } _ { \mathrm { F } }$
- 在截止频率,ƒ=ƒc 时, $\frac { Vout } { \operatorname { Vin } } = \frac { A _ { F } } { \sqrt { 2 } } = 0.707 \mathrm { A } _ { \mathrm { F } }$
- 在非常高的频率下,ƒ>ƒc 时, $ \frac { \text { Vout } } { \text { Vin } } < A _ { F } $
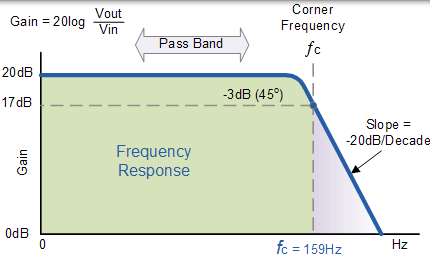
因此,有源低通滤波器具有从 0Hz 到截止点 ƒC 不变的增益 AF 。在 ƒC 增益为 0.707AF,在 ƒC 之后它随着频率的增加以恒定的速率下降。也就是说,当频率增加 10 倍时,电压增益减小为原来的 1/10。
换句话说,每当频率增加 10 时,增益会降低 20dB= 20 * log(10)。当处理滤波器电路时,电路的通带增益的幅度通常以分贝或 dB 表示为电压增益的函数,定义如下:
电压增益幅度(dB)
$$ \begin{array} { c } { \mathrm { AV } ( \mathrm { dB } ) = 20 \log _ { 10 } \left( \frac { \mathrm { Vout } } { \mathrm { Vin } } \right) } \\ { \therefore - 3 \mathrm { dB } = 20 \log _ { 10 } \left( 0.707 \frac { \mathrm { Vout } } { \mathrm { Vin } } \right) } \end{array} $$
有源低通滤波器示例 No1
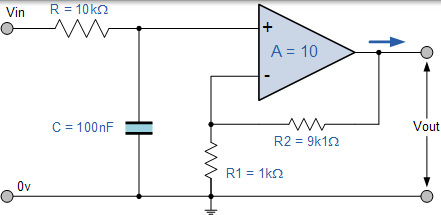
设计一种同相有源低通滤波器电路,其低频增益为 10,高频截止转角频率为 159Hz,输入阻抗为 10KΩ。
非反相运算放大器的电压增益如下:
$$ A _ { F } = 1 + \frac { R _ { 2 } } { R _ { 1 } } = 10 $$
假设电阻器 R1 的值为 1kΩ,重新排列上面的公式给出 R2 的值 :
$$ R _ { 2 } = ( 10 - 1 ) x R _ { 1 } = 9 x | k \Omega = 9 k \Omega $$
然后,对于 10 倍的电压增益,R1 =1kΩ,R2 =9kΩ。但是,不存在 9kΩ 电阻,因此使用下一个优选值 9k1Ω。
将此电压增益转换为分贝 dB 值可得出:
$$ \text {Gain in } d B = 20 \log A = 20 \log 10 = 20 d B $$
截止频率( ƒc )为 159Hz,输入阻抗为 10kΩ。可以使用以下公式计算截止频率:
$$ f _ { C } = \frac { 1 } { 2 \pi R C } H z $$
其中,$f _ { C } = 159 \mathrm { Hz } ) $ and $ ( \mathrm { R } = 10 \mathrm { K } \Omega $
然后,通过重新排列上面的公式,我们可以找到电容器 C 的值 :
$$ C = \frac { 1 } { 2 \pi f c R } = \frac { 1 } { 2 \pi x 159 \times 10 k \Omega } = 100 n F $$
然后,最终电路及其频率响应如下:
低通滤波器电路
频率响应曲线
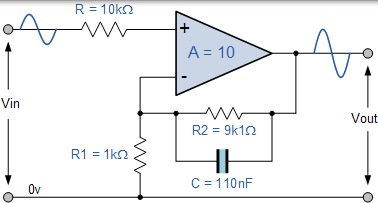
如果连接到电路输入的外部阻抗发生变化,则此变化也会影响滤波器的转角频率(串联或并联连接的元件)。避免这种情况的一种方法是将电容器与反馈电阻器 R2 并联。
考虑电阻值是 9k1Ω ,电容值将从 100nF 略微变化到 110nF,用于计算截止转角频率的公式与用于 RC 无源低通滤波器的公式相同。
$$ f _ { C } = \frac { 1 } { 2 \pi C R _ { 2 } } \text { Hertz } $$
有源低通滤波器电路的一个例子如下。
简化的非反相放大器滤波电路
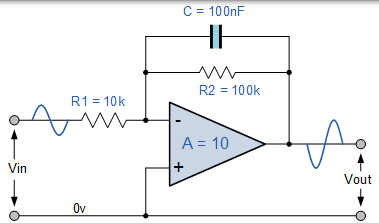
等效反相放大器滤波电路
应用有源低通滤波器是在音频放大器,均衡器或扬声器系统向低频低音信号引导至较大的低音扬声器或以减少任何高频噪声或“嘶嘶”类型的失真。当在音频应用中使用这样的时,有源低通滤波器有时被称为“低音增强”滤波器。
二阶低通有源滤波器
与无源滤波器一样,只需在输入路径中使用额外的 RC 网络,即可将一阶低通有源滤波器转换为二阶低通滤波器。二阶低通滤波器的频率响应与一阶类型的频率响应相同,不同之处在于阻带衰减将是 的一阶滤波器的两倍 - 40dB/decade(12dB /octave)。因此,二阶有源低通滤波器所需的设计步骤是相同的。
二阶有源低通滤波器电路

当将滤波器电路级联在一起以形成高阶滤波器时,滤波器的总增益等于每级的乘积。例如,一级的增益可以是 10,第二级的增益可以是 32,第三级的增益可以是 100,然后总增益将是 32,000,(10 x 32 x 100),如下所示。
级联电压增益

$$ \begin{aligned} \mathrm { Av } & = \mathrm { Av } _ { 1 } \times \mathrm { Av } _ { 2 } \times \mathrm { AV } _ { 3 } \\ \mathrm { Av } ( \mathrm { dB } ) & = 20 \log _ { 10 } ( 32,000 ) \\ \mathrm { Av } ( \mathrm { dB } ) & = 90 \mathrm { d } \mathrm { B } \\ \mathrm { Av } ( \mathrm { dB } ) & = 90 d B \\ 90 \mathrm { d } \mathrm { B } & = 20 \mathrm { d } \mathrm { B } + 30 \mathrm { d } \mathrm { B } + 40 \mathrm { d } \mathrm { B } \end{aligned} $$
二阶(两极)有源滤波器很重要,因为可以使用它们设计高阶滤波器。通过将一阶和二阶滤波器级联在一起,可以构造具有奇数或甚至高达任何值的阶数值的滤波器。在下一个关于滤波器的教程中,我们将看到有源高通滤波器可以通过反转电路中电阻和电容的位置来构建。