有源高通滤波器

通过将无源 RC 滤波器网络与运算放大器组合以产生具有放大的高通滤波器,可以创建有源高通滤波器。
有源高通滤波器 (HPF) 的基本操作与其等效 RC 无源高通滤波器电路相同,不同之处在于该电路具有运算放大器包含在其设计中,提供放大和增益控制。
与之前的有源低通滤波器电路一样,最简单形式的有源高通滤波器是将标准反相或非反相运算放大器连接到基本 RC 高通无源滤波器电路,如图所示。
一阶高通滤波器
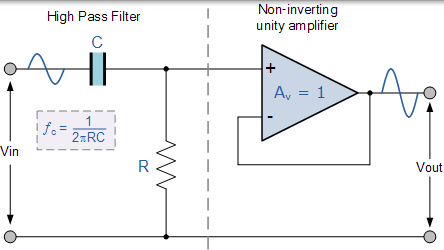
从技术上讲,没有有源高通滤波器这样的东西。与具有“无限”频率响应的无源高通滤波器不同,有源高通滤波器的最大通带频率响应受到所使用的运算放大器的开环特性或带宽的限制,使得它们看起来好像是带通滤波器,具有高频截止频率,由运算放大器和增益的选择决定。
在运算放大器教程中,我们看到运算放大器的最大频率响应仅限于增益/带宽乘积或正在使用的运算放大器的开环电压增益( AV ),从而使其具有带宽限制,其中闭环运算放大器的响应与开环响应相交。
一个常用的运算放大器,如 uA741,具有典型的“开环”(无任何反馈),最大约 100dB 的直流电压增益,随着作为输入频率的增加增益以 -20dB / Decade(-6db / Octave)的滚降率降低。uA741 的增益降低,直到达到单位增益(0dB)或其交叉频率 ƒt (约为 1MHz)。这使得运算放大器的频率响应曲线与一阶低通滤波器的频率响应曲线非常相似,如下所示。
典型运算放大器的频率响应曲线
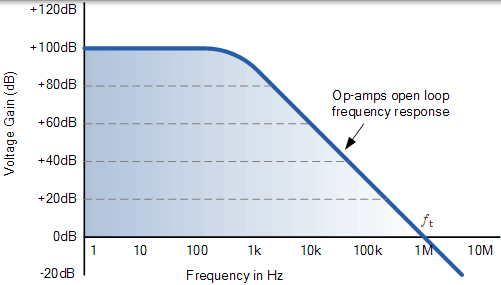
然后,高频“高通滤波器”的性能受到该单位增益交叉频率的限制,该交叉频率决定了开环放大器的总带宽。对于高速数字视频放大器,运算放大器的增益带宽积从大约 100kHz 开始,小信号放大器高达约 1GHz,基于运算放大器的有源滤波器可以实现非常好的精度和性能,前提是低容差电阻器和电容器使用。
在正常情况下,闭环有源高通或带通滤波器所需的最大通带远低于最大开环转换频率。但是,在设计有源滤波器电路时,为电路选择正确的运算放大器非常重要,因为高频信号的丢失可能会导致信号失真。
有源高通滤波器
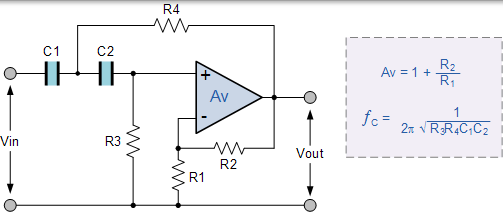
顾名思义,一阶(单极) 有源高通滤波器衰减低频并传递高频信号。它仅由无源滤波器部分和非反相运算放大器组成。电路的频率响应与无源滤波器的频率响应相同,不同之处在于信号的幅度通过放大器的增益增加,而对于非反相放大器,通带电压增益的值为 1 + R2 / R1,与低通滤波器电路相同。
具有放大功能的有源高通滤波器
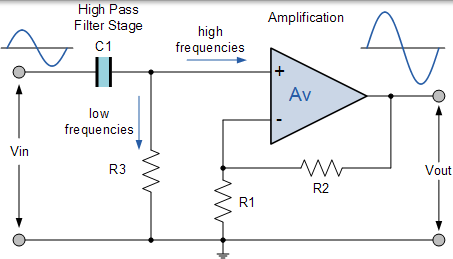
一阶高通滤波器仅由无源滤波器和非反相放大器组成。除了通过放大器的增益增加信号的幅度之外,电路的频率响应与无源滤波器的频率响应相同。
对于非反相放大器电路,滤波器的电压增益幅度作为反馈电阻( R2 )除以其相应的输入电阻( R1 )的函数给出,并如下所示:
增益有源高通滤波器
$$ \text { Voltage Gain, } ( \mathrm { Av } ) = \frac { \mathrm { Vout } } { \mathrm { Vin } } = \frac { \mathrm { A } _ { \mathrm { F } } \left( \frac { f } { f \mathrm { c } } \right) } { \sqrt { 1 + \left( \frac { f } { f \mathrm { c } } \right) ^ { 2 } } } $$
其中,
- AF =滤波器的通带增益,( 1 + R2 / R1 )
- ƒ = 输入信号的频率,单位为赫兹,(Hz)
- ƒc = 以赫兹为单位的截止频率,(Hz)
就像低通滤波器一样,高通有源滤波器的工作可以从上面的频率增益公式中验证:
- 在非常低的频率下,ƒ < ƒc 时,$\frac { \mathrm { Vout } } { \mathrm { Vin } } < \mathrm { A } _ { \mathrm { F } }$
- 在截止频率,ƒ = ƒc 时,$\frac { ) Vout ( } { V ) in ( } = \frac { A _ { F } } { \sqrt { 2 } } = 0.707 \mathrm { A } _ { \mathrm { F } }$
- 在非常高的频率下,ƒ > ƒc 时, \frac { \mathrm { Vout } } { \mathrm { Vin } } \cong \mathrm { A } _ { \mathrm { F } }
然后,有源高通滤波器增益 AF 从 0Hz 增加到低频截止点 ƒC,随着频率的增加以 20dB /decade 增加。在 ƒC 处,增益是 0.707 * AF, ƒC 之后的所有频率都是通带频率,从而滤波器具有恒定的增益 AF, 最高频率由运算放大器的闭环带宽决定。
在处理滤波器电路时,电路通带增益的幅度通常以分贝或 dB 表示,作为电压增益的函数,这被定义为:
电压增益幅度(dB)
$$ \begin{array} { c } { \mathrm { Av } ( \mathrm { dB } ) = 20 \log _ { 10 } \left( \frac { \mathrm { Vout } } { \mathrm { Vout } } \right) } \\ { \therefore - 3 \mathrm { dB } = 20 \log _ { 10 } \left( 0.707 \frac { \mathrm { Vout } } { \mathrm { Vin } } \right) } \end{array} $$
对于一阶滤波器,滤波器的频率响应曲线增加 20dB / decade 或 6dB /Octave,直到确定的截止频率点,该截止频率点始终低于最大增益值 -3dB。与之前的滤波器电路一样,可以使用相同的公式找到较低的截止频率( ƒc ):
$$ f _ { C } = \frac { 1 } { 2 \pi R C } \textrm {Hz} $$
输出信号的相应相位角或相移与无源 RC 滤波器的相位相位或相移相同,并超前输入信号的相位角或相移。它在截止频率 ƒc 值处等于 +45o,如下所示:
$$ \text { Phase Shift } \phi = \tan ^ { - 1 } \left( \frac { 1 } { 2 \pi / R C } \right) $$
也可以使用反相运算放大器配置来制作简单的一阶有源高通滤波器,并且给出该电路设计的示例以及其对应的频率响应曲线。假设电路增益为 40dB。
反相运算放大器电路
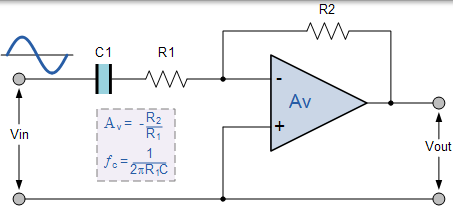
频率响应曲线

有源高通滤波器示例 No1
一阶有源高通滤波器的通带增益为 2,截止频率为 1kHz。如果输入电容的值为 10nF,根据截止频率来确定电阻和反馈网络中的增益电阻的值。另外,绘制滤波器的预期频率响应。
截止转角频率为 1kHz,电容为 10nF,因此 R 的值为 :
$$ \mathrm { R } = \frac { 1 } { 2 \pi f _ { \mathrm { c } } \mathrm { C } } = \frac { 1 } { 2 \pi .1000 .10 \times 10 ^ { - 9 } } = 15.92 \mathrm { kS } $$
或选择最接近的首选值 - 16kΩ。
因此,滤波器的通带增益 AF 因此为2。
$$ \mathrm { A } _ { \mathrm { F } } = 1 + \frac { \mathrm { R } _ { 2 } } { \mathrm { R } _ { 1 } } , \quad \therefore 2 = 1 + \frac { \mathrm { R } _ { 2 } } { \mathrm { R } _ { 1 } } \quad \text { and } \quad \frac { \mathrm { R } _ { 2 } } { \mathrm { R } _ { 1 } } = 1 $$
电阻值 R2 除以电阻值 R1 的值为 1。然后,电阻器 R1 必须等于电阻器 R2,因为通带增益 AF = 2。因此,我们可以为两个电阻选择合适的值,例如,每个电阻为 10kΩ,用于两个反馈电阻。
因此,对于具有为 1kHz 的截止转角频率的高通滤波器,R 和 C 的值将分别是 10kΩ 和 10nF。产生两个通带增益的两个反馈电阻的值如下: R1 = R2 =10kΩ。
频率响应波特图的数据可以通过将上面获得的值在 100Hz 到 100kHz 的频率范围内代入电压增益的等式来获得:
$$ \text { Voltage Gain, } ( \mathrm { Av } ) = \frac { \text { Vout } } { \mathrm { Vin } } = \frac { \mathrm { A } _ { \mathrm { F } } \left( \frac { f } { f \mathrm { c } } \right) } { \sqrt { 1 + \left( \frac { f } { f \mathrm { c } } \right) ^ { 2 } } } $$
然后,这将为我们提供以下数据表。
| 频率 f(Hz) | 电压增益 ( Vo / Vin ) | 增益(dB) 20log( Vo / Vin ) |
|---|---|---|
| 100 | 0.20 | -14.02 |
| 200 | 0.39 | -8.13 |
| 500 | 0.89 | -0.97 |
| 800 | 1.25 | 1.93 |
| 1000 | 1.41 | 3.01 |
| 3000 | 1.90 | 5.56 |
| 5000 | 1.96 | 5.85 |
| 10000 | 1.99 | 5.98 |
| 50000 | 2.00 | 6.02 |
| 100000 | 2.00 | 6.02 |
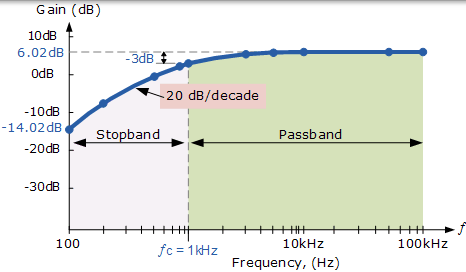
现在可以如下所示绘制上表中的频率响应数据。在阻带(从 100Hz 到 1kHz),增益以 20dB / decade 的速率增加。但是,在截止频率ƒC = 1kHz 后的通带,增益保持在恒定 6.02 分贝。通带的频率上限由我们前面讨论过的运算放大器的开环带宽决定。然后滤波器电路的波特图将如下所示。
例子的频率响应波特图
应用有源高通滤波器是在音频放大器,均衡器或扬声器系统的高频信号引导到较小的高音扬声器或以减少任何低频噪声或“隆隆声”类型的失真。当在音频应用中使用这样的时,有源高通滤波器有时被称为“高音增强”滤波器。
二阶高通有源滤波器
与无源滤波器一样,只需在输入路径中使用额外的 RC 网络,即可将一阶高通有源滤波器转换为二阶高通滤波器。二阶高通滤波器的频率响应与一阶类型的频率响应相同,只是阻带衰减将是一阶滤波器的两倍 - 40dB /decade(12dB/Octave)。因此,二阶有源高通滤波器所需的设计步骤是相同的。
二阶有源高通滤波器电路
通过将第一和第二阶滤波器级联在一起,简单地形成高阶高通有源滤波器,例如3阶,4阶等。例如,通过级联一阶和二阶滤波器形成三阶高通滤波器,通过将两个二阶滤波器级联在一起形成四阶高通滤波器,依此类推。
然后,具有偶数序号的有源高通滤波器将仅包含二阶滤波器,而奇数阶数将从开头的一阶滤波器开始,如图所示。
级联有源高通滤波器
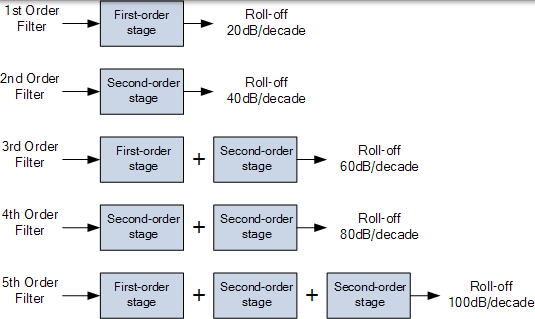
尽管对可以形成的滤波器的顺序没有限制,但是随着滤波器的阶数增加而其尺寸也增加。而且,其精度下降,即实际阻带响应与理论阻带响应之间的差异也增加。
如果频率确定电阻器全部相等,R1 = R2 = R3 等,并且频率确定电容器全部相等,C1 = C2 = C3 等,那么任何滤波器阶数的截止频率将完全相同。然而,高阶滤波器的总增益是固定的,因为所有频率确定分量都相等。
在下一个关于滤波器的教程中,我们将看到有源带通滤波器可以通过将高通和低通滤波器级联在一起来构建。