电容分压器

分压器电路可以由无功元件构成，就像它们可以由固定值电阻器构成一样容易。

但就像电阻电路一样，电容分压器网络不会受到电源频率变化的影响，即使它们使用的是电容元件，因为串联链中的每个电容器都会受到电源频率变化的影响。

但在我们更详细地研究电容分压器电路之前，我们需要更多地了解容性电抗以及它如何影响不同频率的电容。

在我们关于电容器的第一篇教程中，我们看到一个电容器由两个平行的导电板组成，这两个导电板由一个绝缘体隔开，在一个板上有一个正（+）电荷，在另一个板上有一个相反的负（-）电荷。我们还看到，当连接到 DC（直流）电源时，一旦电容器完全充电，绝缘体（称为电介质）就会阻挡通过它的电流。

典型电容器

电容器就像电阻器一样阻止电流流动，但与电阻器以热量的形式耗散其不需要的能量不同，电容器在充电时释放能量，并在放电时释放能量或将能量释放回连接电路。

电容器通过在其板上存储电荷来抵抗或“反应”电流的能力被称为“电抗”，并且因为该电抗涉及电容器，因此称为电容电抗 （ Xc），并且类似电阻，电抗是也用欧姆来衡量。

当完全放电的电容器连接在诸如电池或电源的 DC 电源上时，电容器的电抗最初非常低，并且当电容器板以指数方式充电时，最大电路电流流过电容器非常短的时间。

在等于大约 5RC 或 5 个时间常数的一段时间之后，电容器的极板充满电，等于电源电压，并且没有其他电流流动。此时，电容器对直流电流的电抗在兆欧区域内达到最大值，几乎是开路，这就是电容器阻断直流的原因。

现在，如果我们将电容器连接到连续反转极性的 AC（交流电）电源，则对电容器的影响是其电路板与所施加的交流电源电压相关地连续充电和放电。这意味着充电和放电电流总是流入和流出电容器板，如果我们有电流，我们还必须具有电抗值来抵抗它。但它的价值是什么，以及决定容抗的价值的因素。

在关于电容和电荷的教程中，我们看到电容器板上存在的电荷量（ Q）与电容器的施加电压和电容值成比例。当施加的交流电源电压（ Vs）值不断变化时，板上的电荷也必须改变值。

如果电容器具有较大的电容值，那么对于给定的电阻，R 对电容器充电需要更长的时间，因为 τ= RC，这意味着充电电流流动的时间更长。对于给定频率，较高的电容导致较小的电抗值 Xc。

同样，如果电容器具有小的电容值，则需要较短的 RC 时间常数来对电容器充电，这意味着电流将流动较短的时间段。电容越小，电抗值 Xc 越高。然后我们可以看到，较大的电流意味着较小的电抗，较小的电流意味着较大的电抗。因此，电容性电抗是反比于电容器的电容值，XC α -1C.

然而，电容不是决定容抗的唯一因素。如果施加的交流电流处于低频，则电抗具有更多的时间来累积给定的 RC 时间常数，并且反对指示大的电抗值的电流。同样地，如果施加的频率高，则在充电和放电循环之间几乎没有时间来建立电抗并且抵抗电流导致更大的电流，这表明电抗更小。

然后我们可以看到电容器是阻抗，并且该阻抗的幅度取决于频率。因此，较大的频率意味着较小的电抗，较小的频率意味着较大的电抗。因此，电容电抗，Xc（其复阻抗）与电容和频率成反比，容抗的标准公式如下：

电容电抗公式

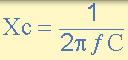
• 哪里：
• Xc =以欧姆表示的电容电抗，（Ω）
• π （pi）= 3.142 的数值常数
• ƒ =以赫兹为单位的频率，（Hz）
• C =法拉的电容，（F）

串联电容器中的电压分布

现在我们已经看到了对电容器充电和放电电流的反对如何不仅取决于其电容值而且取决于电源的频率，让我们看看它如何影响两个串联的电容器，形成一个电容分压器电路。

电容分压器

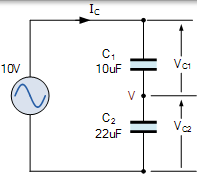
考虑两个电容器 C1 和 C2 串联连接在 10 伏的交流电源上。由于两个电容器是串联的，电荷 Q 上它们是相同的，但是在它们之间的电压将是不同的并涉及它们的电容值，如 V = Q / C。

分压器电路可以由无功元件构成，就像它们可以由电阻器构造一样容易，因为它们都遵循分压器规则。以此电容分压电路为例。

可以以多种方式计算每个电容器两端的电压。一种方法是找到每个电容器的容抗，总电路阻抗，电路电流，然后用它们来计算电压降，例如：

电容分压器实例 No1

在上面的串联电路中使用 10uF 和 22uF 的两个电容，计算每个电容器在 80Hz 时的 10 伏有效值电压下的有效值电压降。

10uF 电容器的电容电抗

22uF 电容器的电容电抗

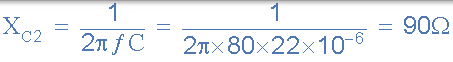
串联电路的总容性电抗 - 请注意，串联的电阻与电阻串联在一起。

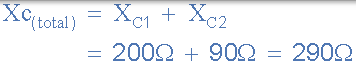
要么：

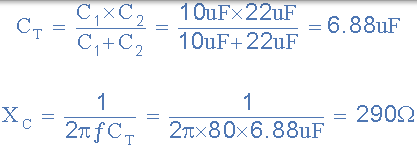
电路电流

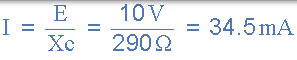
然后，串联电容分压器中每个电容的电压降将为：

当电容器值不同时，较小值的电容器将自身充电至比较大值的电容器更高的电压，并且在上面的示例中，这分别是 6.9 和 3.1 伏。由于基尔霍夫电压定律适用于该电路和每个串联电路，因此各个电压降的总和将等于电源电压的值，VS 和 6.9 + 3.1 确实等于 10 伏。

注意，无论电源频率如何，串联电容分压器电路中连接的两个电容器上的电压降的比率将始终保持不变。然后，即使供电频率从 80Hz 增加到 8000Hz，如图所示，在我们的简单示例中，上面的 6.9 伏和 3.1 伏的两个电压降也将保持不变。

电容分压器实例 No2

使用相同的两个电容器，计算 8,000Hz(8kHz) 的电容电压降。

虽然两个电容器两端的电压比可以保持不变，但随着电源频率的增加，组合的容抗电阻会降低，因此总电路阻抗也会降低。阻抗的减小导致更多电流流动。例如，在 80Hz 时，我们计算出上面的电路电流约为 34.5mA，但在 8kHz 时，电源电流增加到 3.45A，增加了 100 倍。因此，流过电容分压器的电流与频率成比例或 Iαƒ 。

我们在这里看到，电容分压器是串联电容器的网络，每个电容器都有一个交流压降。由于电容分压器使用电容器的容抗值来确定实际电压降，因此它们只能用于频率驱动电源，因此不能用作直流分压器。这主要是由于电容器阻断 DC 并因此没有电流流动的事实。

电容分压器电路用于各种电子应用，从 Colpitts 振荡器到电容式触摸屏，当人手指触摸时改变输出电压，用作降低高压等电源变压器的廉价替代品，如在使用低压电子设备或 IC 等的电源连接电路中。

因为我们现在知道，两个电容器的电抗随频率变化（以相同的速率），因此电容分压器电路上的分压将始终保持不变，保持稳定的分压器。