串联 RLC 电路分析
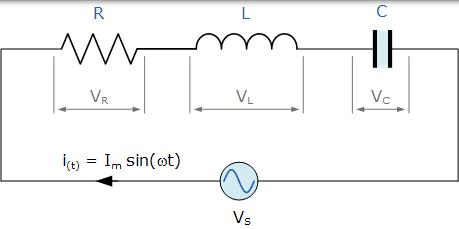
RLC 系列电路由交流电源串联的电阻,电容和电感组成
到目前为止,我们已经看到三个基本的无源元件: 电阻,电感和电容*在连接到正弦交流电源时彼此具有非常不同的相位关系。
在纯欧姆电阻器中,电压波形与电流“同相”。在纯电感电压波形“导致”目前由 90o,给我们的表达:ELI。在纯电容中,电压波形“滞后”电流 90o,给出了表达式:ICE。
这个相位差,Φ 取决于所使用的元件的无功值,并且希望现在我们知道电抗,( X)如果电路元件是电阻则为零,如果电路元件是电感元件则为正,如果电容元件是电容元件则为负给出它们产生的阻抗:
元素阻抗
| 电路元件 | 阻力,(R) | 电抗,(X) | 阻抗,(Z) |
| 电阻 | [R | 0 | 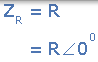 |
| 感应器 | 0 | ωL | 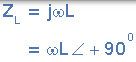 |
| 电容器 | 0 | 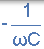 |
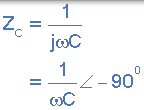 |
我们可以将所有三个组合在一起成为一串联 RLC 电路,而不是分别分析每个无源元件。一串联 RLC 电路的分析与我们之前看到的双串联 RL 和 RC 电路的分析相同,除了这次我们需要考虑 XL 和 XC 的幅度来找到整个电路电抗。串联 RLC 电路被归类为二阶电路,因为它们包含两个储能元件,即电感大号和电容 C ^ 。考虑下面的 RLC 电路。
串联 RLC 电路

上面的串联 RLC 电路具有单个环路,流过环路的瞬时电流对于每个电路元件是相同的。由于电感和电容电抗的 XL 和 XC 是电源频率的函数,因此串联 RLC 电路的正弦响应将随频率 f 而变化。然后,R,L 和 C 元件的每个电路元件上的各个电压降将彼此“异相”,如下所定义:
- i(t) = Imax sin(ωt)
- 纯电阻器 VR 上 的瞬时电压与电流“同相”
- 纯电感器上的瞬时电压 VL “导通”电流 90o
- 纯电容器上的瞬时电压 VC “滞后”电流 90o
- 因此,VL 和 VC ^ 是 180o “外的相位”,并在彼此相对。
对于上面的 RLC 系列电路,可以显示为:

串联 RLC 电路中所有三个元件的源极电压幅度由三个独立的分量电压 VR,VL 和 VC 组成,其中所有三个元件共用电流。因此,矢量图将具有电流矢量作为其参考,其中三个电压矢量相对于该参考绘制,如下所示。
各个电压矢量

这意味着我们不能简单地将 VR,VL 和 VC 加在一起以找到所有三个分量上的电源电压 VS,因为所有三个电压矢量指向关于电流矢量的不同方向。因此,我们必须找到电源电压 VS 作为三个分量电压的矢量和,它们组合在一起。
环路和节点电路的基尔霍夫电压定律(KVL)表明,在任何闭环周围,环路周围的电压降之和等于 EMF 的总和。然后将这个定律应用于这三个电压将给出我们的源电压幅度,VS as。
串联 RLC 电路的瞬时电压
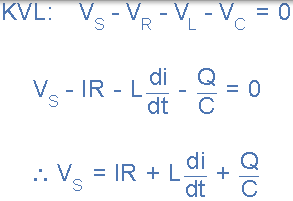
通过将上述三个单独的相量组合在一起并矢量地添加这些电压来产生串联 RLC 电路的相量图。由于流过电路的电流对于所有三个电路元件是共同的,因此我们可以将其用作参考矢量,其中三个电压矢量以相应的角度相对于此绘制。
将得到的矢量 VS 通过添加在一起的两个向量,所获得的 VL 和 VC ^,然后加入此总和到其余矢量 VR。在 VS 和 i 之间获得的最终角度将是电路相位角,如下所示。
串联 RLC 电路的相量图
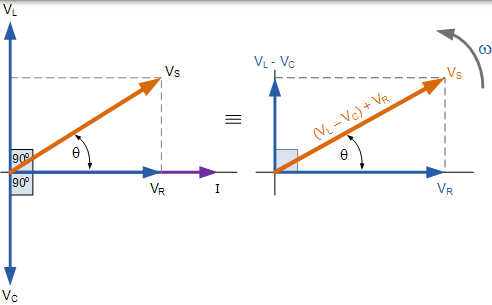
从右上方的相量图可以看出,电压矢量产生一个矩形三角形,包括斜边 VS,水平轴 VR 和垂直轴 VL - VC 希望你会注意到,这形成了我们的老最喜欢的电压三角因此,我们可以利用这个电压三角形毕达哥拉斯定理在数学上获得的价值 VS,如图所示。
串联 RLC 电路的电压三角形
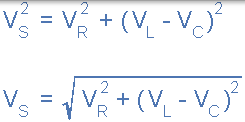
请注意,使用上述公式时,最终的无功电压必须始终为正值,即最小电压必须始终从最大电压中取出,我们不能将负电压加到 VR 上, 因此它是正确的有 VL - VC 或 VC - VL。最大的最小值,否则计算 VS 将是不正确的。
我们从上面知道,电流在一串联 RLC 电路的所有元件中具有相同的幅度和相位。然后,也可以根据流过的电流和每个元件两端的电压数学地描述每个元件两端的电压。
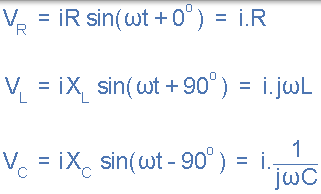
通过将这些值代入上面的毕达哥拉斯方程中的电压三角形将给我们:
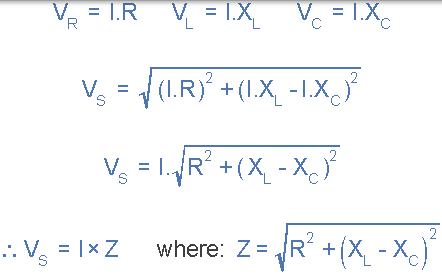
因此我们可以看到源电压的幅度与流过电路的电流的幅度成比例。该比例常数称为电路的阻抗,其最终取决于电阻以及电感和电容电抗。
然后,在上述的串联 RLC 电路,可以看出的是,反对电流流动是由三个部分组成,XL,XC 和 - [R 与电抗,XT 任何 RLC 串联电路被定义为: XT = XL - XC 或 XT = XC - X.L 哪个更大。因此,电路的总阻抗被认为是驱动电流通过它所需的电压源。
串联 RLC 电路的阻抗
由于三个矢量电压彼此异相,因此 XL,XC 和 R 也必须彼此“异相”,R,XL 和 XC 之间的关系是矢量和这三个组成部分。这将使我们的 RLC 电路总阻抗, Z 。这些电路阻抗可以用阻抗三角形绘制和表示 **** 如下所示。
串联 RLC 电路的阻抗三角形
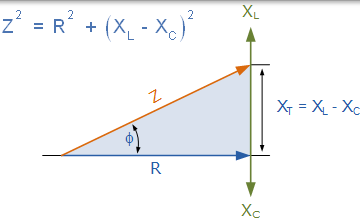
串联 RLC 电路的阻抗 Z 取决于角频率 ω,XL 和 XC 也是如此。 如果容抗大于感抗,XC > XL 则整个电路电抗是电容性的,给出一个超前相角。
同样,如果感抗小于容抗,XL > XC 则整个电路电抗是电感性的,从而使串联电路具有滞后相位角。如果这两个电抗的是相同的,XL = XC 然后发生这种情况被称为共振频率,并产生效果的角频率共振,我们将看更详细的另一个教程。
那么电流的大小取决于施加到串联 RLC 电路的频率。当阻抗 Z 处于其最大值时,电流是最小值,同样,当 Z 处于其最小值时,电流处于最大值。所以上面的阻抗方程可以重写为:
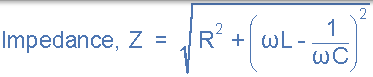
源电压 VS 和电流 i 之间的相位角 θ 与阻抗三角形中 Z 和 R 之间的角度相同。取决于源电压是否超前或滞后电路电流,该相位角可以是正值或负值,并且可以从阻抗三角形的欧姆值数学计算为:
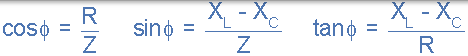
串联 RLC 电路实例 No1
包含 12Ω 电阻,0.15H 电感和 100uF 电容的串联 RLC 电路串联连接在 100V,50Hz 电源上。计算总电路阻抗,电路电流,功率因数和绘制电压相量图。
感抗,XL。

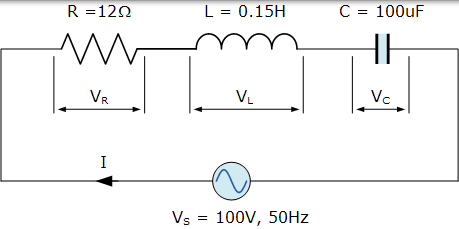
容抗,XC。
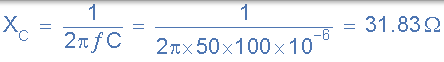
电路阻抗,Z。
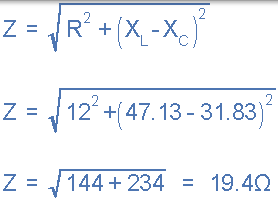
电路电流 I 。

在串联 RLC 电路,电压 VR,VL,VC。
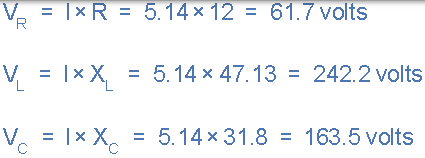
电路功率因数和相角 θ。
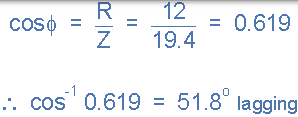
相量图。
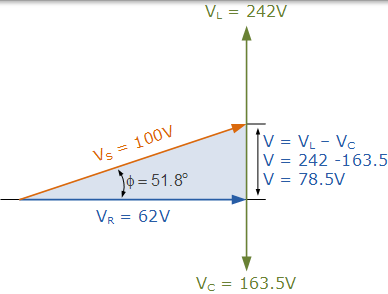
由于相位角 θ 作为 51.8 正值计算o 电路的总电抗必须是电感性的。由于我们已经将电流矢量作为我们在串联 RLC 电路中的参考矢量,然后电流“滞后”源电压 51.8o 所以我们可以说相位角是滞后的,这由我们的助记符表达式 ELI 证实。
串联 RLC 电路概述
在包含电阻器,电感器和电容器的串联 RLC 电路中,源电压 VS 是由三个分量 VR,VL 和 VC 组成的相量和,其中三个分量电流共用。由于电流对于所有三个组件是共同的,因此在构造电压三角形时将其用作水平参考。
电路的阻抗是与电流的完全相反。对于串联 RLC 电路,可以通过将电压三角形的每一侧除以其电流 I 来绘制阻抗三角形。到在电阻元件上的电压降等于 I * R,在这两个反应性元件上的电压是 I * X = I * XL I * X -C 而源极电压等于余* Z。VS 和 I 之间的角度将是相位角, θ。
当使用包含多个电阻的串联 RLC 电路时,电容或电感要么纯净,要么不纯,它们可以全部加在一起形成单个元件。例如,所有电阻加在一起,RT =(R1 + R2 + R3) …等或所有电感的 LT =(L1 + L2 + L3) ……这样,包含许多元件的电路可以很容易地减少到单个阻抗。
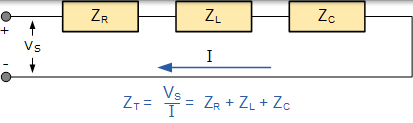
在下一个关于并联 RLC 电路的教程中,我们将看一下当并联电路配置时,在并联电路配置中连接在一起的三个组件的电压 - 电流关系以及相应的相量图表示。我们还将首次介绍入场的概念。