相位差和相移

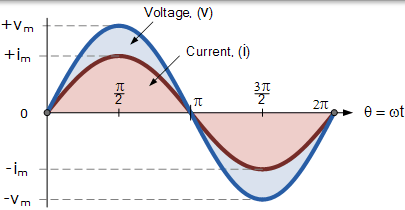
相位差用于描述当两个或更多个交流量达到其最大值或零值时的度数或弧度的差异。

之前我们看到正弦波形是一个交变量，可以在时域中沿水平零轴以图形方式显示。我们还看到，作为交变量，正弦波在时间 π/ 2 处具有正的最大值，在时间 3π/ 2 处具有负的最大值，在 0，π 和 2π 处出现零值。

但是，并非所有正弦波形都同时通过水平轴零点，与另一个正弦波相比，可能会向某个值 移位到 0o 的右侧或左侧。

例如，将电压波形与电流波形进行比较。然后，这产生两个正弦波形之间的角度偏移或相位差。在 t = 0 时没有通过零的任何正弦波都具有相移。

正弦波形的相位差或相移用角度 Φ （希腊字母 Phi）来表示，以度或弧度表示波形已经从某个参考点沿水平零轴偏移。换句话说，相移是沿公共轴的两个或更多个波形之间的横向差异，并且相同频率的正弦波形可以具有相位差。

交流波形的相位差 Φ 可以在 0 到其最大时间周期 T 之间变化，在一个完整周期 T 期间波形可以是沿水平轴的任何位置， Φ= 0 到 2π （弧度）或 Φ= 0 到 360o，取决于所使用的角度单位。

相位差还可以表示为时间偏移的 T （秒）表示周期 T 的一小部分，例如，+ 10ms 或- 50us，但通常更常见的是用角度来表达相位差的。

然后，需要修改我们在先前的正弦波形中产生的正弦电压或电流波形的瞬时值的等式，以考虑波形的相位角，并且这个新的一般表达式变为。

相位差方程

$$ A _ { ( t ) } = A _ { \max } \times \sin ( \omega t \pm \Phi ) $$

其中，

• Am - 是波形的幅值。
• ωt - 是以弧度/秒为单位的波形的角频率。
• Φ - 是波形从参考点向左或向右偏移的以度或弧度表示的相位角。

如果正弦波形的正向斜率在 t = 0 之前通过水平轴，则波形向左移动，因此 Φ > 0，并且相位角本质上是正的， +Φ 给出超前相位角。换句话说，它在时间上较早于 0o 出现产生矢量的逆时针旋转。

同样，如果正弦波形的正斜率在 t = 0 之后的某个时间通过水平 x 轴，则波形向右移动，因此 Φ < 0，并且相位角本质上是负的，因为它在时间上稍后出现大于 0o 滞后相位角产生矢量的顺时针旋转。两种情况如下所示。

正弦波形的相位关系

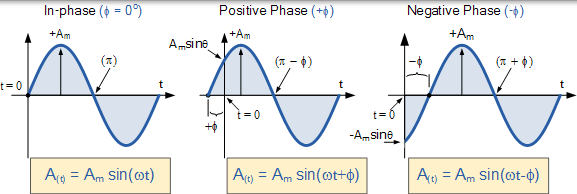
首先，让我们考虑这两个交变量，例如一个电压 v 和电流 I 具有相同的频率 ƒ ，由于两个量的频率与角速度相同，因此 ω 也必须相同。因此，在任何时刻，我们都可以说电压的相位与电流的相位相同。

那么特定时间段内的旋转角度将始终相同，因此两个量 v 和 i 之间的相位差将为零即 Φ= 0。电压 v 和电流 I 它们必须在在同一时间（尽管它们的幅度可以是不同的）都达到它们的最大正、负和零值。然后，两个交变量 v 和 i 被称为同相。

两个正弦波形 - 同相

现在让我们考虑的是，电压，v 和电流 I 有本身之间的相位差 30o，所以（ Φ = 30o 或 π / 6 弧度）。由于两个交变量以相同的速度旋转，即它们具有相同的频率，所以该相位差对于所有时刻都保持恒定，然后两个量之间的相位差 30° 由 Φ 如下图所示。

正弦波形的相位差

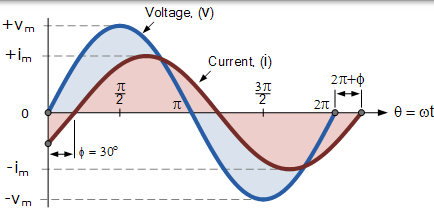
上面的电压波形沿着水平参考轴从零开始，但是在同一时刻，电流波形的值仍为负值，并且直到 30o 后才会越过该参考轴。然后在两个波形之间存在相位差，因为电流越过水平参考轴达到其最大峰值并且在电压波形之后变为零值。

由于这两个波形不再是“同相”，而它们是异相，一个由 Φ 确定的量，在我们的例子中，这是 30o。所以我们可以说这两个波形有相位差 30°。也可以说电流波形在电压波形后面“滞后”相位角 Φ。然后在上面的示例中，两个波形具有**滞后相位差，**因此上面的电压和电流的表达式为，

$$ \begin{array} { c } { \text { Voltage } \left( \mathrm { v } _ { \mathrm { t } } \right) = \mathrm { V } _ { \mathrm { m } } \mathrm { sin } \omega \mathrm { t } } \\ { \text { Current } \left( \mathrm { i } _ { t } \right) = \mathrm { I } _ { \mathrm { m } } \sin ( \omega \mathrm { t } - \theta ) } \end{array} $$

其中，I 滞后 v 角度 Φ。

同样地，如果电流在电压之前的某一时刻达到其最大峰值或零值，那么电流波形将是超前电压一些相位角。然后，两个波形被称为具有超前相位差，并且电压和电流的表达式将是。

$$ \begin{array} { c } { \text { Voltage } \left( \mathrm { v } _ { \mathrm { t } } \right) = \mathrm { V } _ { \mathrm { m } } \mathrm { sin } \omega \mathrm { t } } \\ { \text { Current } \left( \mathrm { i } _ { t } \right) = \mathrm { I } _ { \mathrm { m } } \sin ( \omega \mathrm { t } + \theta ) } \end{array} $$

其中，I 超前 v 角度 Φ。

正弦波的相位角可用于通过使用术语“超前”和“滞后”来描述一个正弦波与另一个正弦波的关系，以指示相同频率的两个正弦波形之间的关系，绘制在同一参考轴上。在我们上面的例子中的两个波形是相移 30o。所以我们可以说 I 滞后于 v 或者我们可以说 v 超前 i 30o，这取决于我们选择哪一个作为参考。

可以沿着水平零轴在任何地方测量两个波形之间的关系以及所得到的相位角，每个波形以相同斜率方向通过正或负。

在交流电源电路中，这种描述同一电路内电压和电流正弦波之间关系的能力非常重要，并构成了交流电路分析的基础。

余弦波形

因此我们现在知道，如果波形与另一个正弦波相比偏移到 0o 的右侧或左侧，则该波形的表达式变为 Am sin(ωt ± Φ) 。但是，如果根据波形穿越水平零轴在参考波形之前 90o 或 π / 2 弧度，该波形被称为余弦波形，而表达式变成了，

余弦表达

$$ \sin \left( \omega t + 90 ^ { \circ } \right) = \sin \left( \omega t + \frac { \pi } { 2 } \right) = \cos ( \omega t ) $$

该余弦波，简称为 COS ，是在电气工程中同正弦波一样重要。余弦波具有相同的形状，它的正弦波对应即它是一个正弦函数，而且偏移 90o ，或在它前面的一个周期的四分之一。

正弦波和余弦波之间的相位差

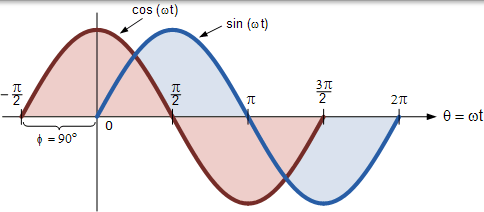
或者，我们也可以说正弦波是一个余弦波，它在另一个方向上移动了 -90o。无论哪种方式，当处理具有角度的正弦波或余弦波时，以下规则将始终适用。

正弦和余弦波关系

$$ \begin{array} { c } { \cos ( \omega \mathrm { t } + \phi ) = \sin \left( \omega \mathrm { t } + \phi + 90 ^ { \circ } \right) } \\ { \sin ( \omega \mathrm { t } + \phi ) = \cos \left( \omega \mathrm { t } + \phi - 90 ^ { \circ } \right) } \end{array} $$

当比较两个正弦波形时，更常见的是将它们的关系表示为具有正向振幅的正弦或余弦，并且这可以使用以下数学恒等式来实现。

$$

• \sin ( \omega \mathrm { t } ) = \sin \left( \omega \mathrm { t } \pm 180 ^ { \circ } \right) \\ - \cos ( \omega t ) = \cos \left( \omega t \pm 180 ^ { \circ } \right) \\ - \cos ( \omega t ) = \sin \left( \omega t \pm 270 ^ { \circ } \right) \\ \pm \sin ( \omega t ) = \cos \left( \omega t \pm 90 ^ { \circ } \right) \pm \cos ( \omega t ) = \sin \left( \omega t \pm 90 ^ { \circ } \right) \\ - \sin ( \omega t ) = \sin ( - \omega t ) \\ \cos ( \omega t ) = \cos ( - \omega t ) $$

通过使用上述这些关系，我们可以将具有或不具有角度或相位差的任何正弦波形从正弦波转换为余弦波，反之亦然。

在下一篇关于相量的教程中，我们将使用一种图形方法，通过查看单相交流量的相量表示以及与两个或多个相量的数学加法相关的一些相量代数来表示或比较两个正弦波之间的相位差。