复数和相量
电气工程中使用的数学用于将电阻、电流或直流电压等相加时,使用的是所谓的“实数”,要么是整数,要么是分数。
但实数并不是我们需要使用的唯一数字,特别是在处理频率相关的正弦波和矢量时。同使用实数一样,复数被引入来求解复数的方程式,用负数的平方根号码来解决,√-1。
在电气工程中,这种类型的数字被称为“虚数”,并且为了将虚数与实数区分开,使用在电气工程中通常用字母 j 作为 j 运算符。因此,字母 j 被放置在实数的前面以表示其虚数操作。
虚数的例子是: j3,j12,j100 等。然后,复数由两个不同但非常相关的部分组成,实数加上虚数。
复数表示二维复数或 s 平面中以两个不同轴为参考的点。横轴称为“实轴”,而纵轴称为“虚轴”。复数的实部和虚部分别缩写为 Re(z) 和 Im(z)。
由实数(有源分量)和虚数(无功分量)数组成的复数可以与基本代数用于分析直流电路完全相同的方式相加、相减。
数学中用于虚数加法或减法的规则和定律与实数相同,j2 + j4 = j6 等。唯一的区别在于乘法,因为两个虚数相乘成为负实数。实数也可以被认为是一个复数,但虚部为零,标记为 j0。
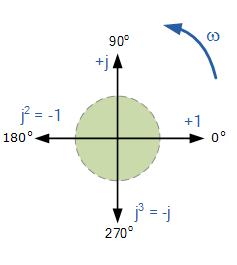
j 运算符的值等于√-1,两个 j 相乘将得到 -1,三个 j 相乘为 -j,四个为 1。由于 j 运算符通常用于指示向量的逆时针旋转,因此每个连续乘法为 j,j2,J3 等,将迫使矢量在逆时针方向上旋转 90o 的固定角度,如下所示。同样地,如果在一个矢量上乘以 -j ,相移将为 -90o,即顺时针方向旋转。
矢量旋转 j 运算符
| 旋转角度 | 矢量表达 |
|---|---|
| 90 | $j ^ { 1 } = \sqrt { - 1 } = + j$ |
| 180 | $j ^ { 2 } = ( \sqrt { - 1 } ) ^ { 2 } = - 1$ |
| 270 | $j ^ { 3 } = ( \sqrt { - 1 } ) ^ { 3 } = - j$ |
| 360 | $j ^ { 4 } = ( \sqrt { - 1 } ) ^ { 4 } = + 1$ |
因此,通过乘以虚数 j2 将逆时针旋转矢量 180o ,乘以 j3 时旋转 270o,乘以 j4 时旋转 360o,或回到其原始位置。乘以 j10 或 j30 将使矢量逆时针旋转适当的量。在每次连续旋转中,矢量的大小始终保持不变。
在电气工程中,有不同的方式以图形或数学方式表示复数。使用余弦和正弦规则的一种方法称为笛卡尔或矩形形式。
使用矩形形式的复数
在上一篇关于相量 的教程中,我们看到一个复数由一个实部和一个虚部表示,它采用以下的通用形式:
$$ Z = x + j y $$
其中,
- Z 是表示矢量的复数
- x 是实数部分或有功部分
- y 是虚部或无功部分
- j 是 √-1
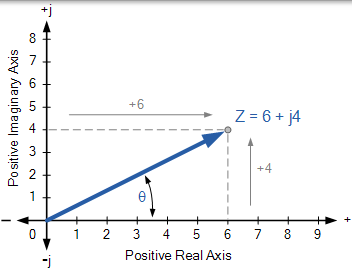
在矩形形式中,复数可以由被称为复数或** s 平面的**二维平面上的点来表示。因此,例如,Z = 6 + j4表示的点,其坐标在水平实轴上是6,在垂直虚轴上是4,如图所示。
使用 Complex 或 s-plane 的复数

但由于矩形形式的复数的实部和虚部都可以是正数或负数,因此实轴和虚轴也必须在正方向和负方向上延伸。然后,这将产生一个复杂的平面,其中有四个象限,称为阿干特图,如下所示。
四象限阿干特图
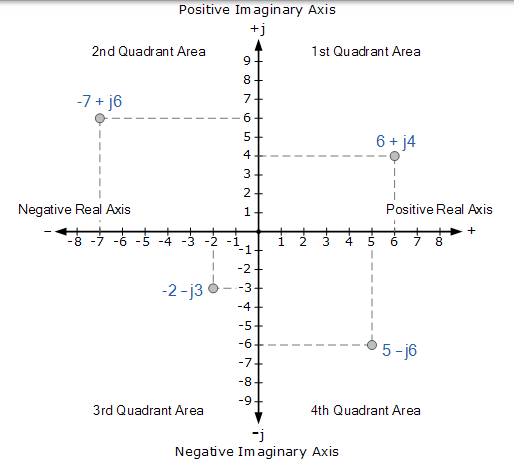
在 Argand 图上,横轴表示垂直虚轴右侧的所有正实数和垂直虚轴左侧的所有负实数。所有正虚数都表示在水平轴上方,而所有负虚数都在水平实轴之下。然后,这产生具有标记为 QI,QII,QIII 和 QIV 的四个不同象限的二维复平面。
上面的 Argand 图也可用于表示旋转相量作为复平面中的一个点,其半径由相量的大小给出,每 2π/ω 秒将围绕它绘制一个完整的圆。
然后,我们可以进一步扩展这种想法来表示复数的定义,同时在极坐标和矩形表示上来表示 90o 的旋转。
$$ \begin{aligned} 0 ^ { \circ } & = \pm 360 ^ { \circ } = + 1 = 1 \angle 0 ^ { \circ } = 1 + j 0 \\ + 90 ^ { \circ } & = + \sqrt { - 1 } = + \mathrm { j } = 1 \angle + 90 ^ { \circ } = 0 + \mathrm { j } 1 \\ - 90 ^ { \circ } & = - \sqrt { - 1 } = - \mathrm { j } = 1 \angle - 90 ^ { \circ } = 0 - \mathrm { j } 1 \\ \pm 180 ^ { \circ } & = ( \sqrt { - 1 } ) ^ { 2 } = - 1 = 1 \angle \pm 180 ^ { \circ } = - 1 + \mathrm { j } 0 \end{aligned} $$
复数也可以具有“零”实部或虚部,例如: Z = 6 + j0 或 Z = 0 + j4。在这种情况下,点直接绘制在实轴或虚轴上。此外,可以使用简单的三角法计算复数的角度以计算直角三角形的角度,或者从正实轴开始围绕 Argand 图逆时针测量。
然后 0 和 90o 的角度在第一象限, 90 和 180o 之间的角度在第二象限。第三象限包括 180 和 270o 之间的角度,而第四象限包括 270 和 360o 之间的角度 等。在所有四个象限中,相关角度可以从以下位置找到:
tan-1(虚部÷实部)
复数的加法和减法
复数的加或减可以数学方式或以矩形形式以图形方式完成。另外,首先将实部加在一起形成和的实部,然后将虚部加在和的虚部上,这个过程如下,用两个复数 A 和 B 作为例子。
复数加法和减法
$$ \begin{array} { c } { A = x + j y \quad B = W + j Z } \\ { A + B = ( x + w ) + j ( y + z ) } \\ { A - B = ( x - W ) + j ( y - z ) } \end{array} $$
复数示例 No1
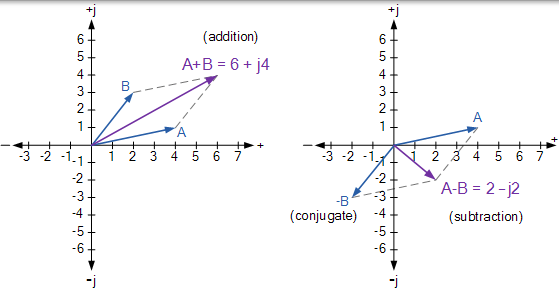
两个矢量分别定义为 A = 4 + j1 和 B = 2 + j3。以矩形( a + jb)形式确定两个矢量的和与差,并以图形方式确定为 Argand 图。
数学加法和减法
- 加法
$$ \begin{array} { l } { A + B = ( 4 + j 1 ) + ( 2 + j 3 ) } \\ { A + B = ( 4 + 2 ) + j ( 1 + 3 ) = 6 + j 4 } \end{array} $$
- 减法
\begin{array} { l } { A - B = ( 4 + j 1 ) - ( 2 + j 3 ) } \\ { A + B = ( 4 - 2 ) + j ( 1 - 3 ) = 2 - j 2 } \end{array}
图形加法和减法
复数的乘法和除法
矩形形式的复数的乘法遵循与正常代数大致相同的规则以及 j 运算符的连续乘法的一些附加规则,其中: j2 = -1。因此,例如将 A = 4 + j1 和 B = 2 + j3 两个向量相乘将得到以下结果。
$$ \begin{aligned} \mathrm { A } \times \mathrm { B } & = ( 4 + j 1 ) ( 2 + j 3 ) \\ & = 8 + j 12 + j 2 + j ^ { 2 } 3 \\ & = 8 + j 14 -3 \\ & = 5 + j 14 \end{aligned} $$
在数学上,矩形形式的复数的除法更难以计算,因为它需要使用分母共轭函数将等式的分母转换为实数。这被称为“合理化”。然后,复数的除法最好使用极坐标进行,我们将在后面介绍。然而,如在矩形形状的例子,我们来计算矢量 A 除以矢量 B 的结果。
$$ \frac { A } { B } = \frac { 4 + j } { 2 + j 3 } $$
分子分母都乘以共轭复数 2 + j3,
$$ \begin{aligned} \frac { 4 + j 1 } { 2 + j } \times \frac { 2 - j 3 } { 2 - j 3 } & = \frac { 8 - j 12 + j 2 - j ^ { 2 } 3 } { 4 - j 6 + j 6 - j ^ { 2 } 9 } \\ & = \frac { 8 - j 10 + 3 } { 4 + 9 } \\ & = \frac { 11 - j 10 } { 13 } \\ & = \frac { 11 } { 13 } + \frac { - j 10 } { 13 } = 0.85 - j 0.77 \end{aligned} $$
复合共轭
共轭复数,通过反转同时保持实数的代数符号相同,将虚数的代数符号取反来得到,用符号$\overline { \textrm {z} }$来表示。例如,Z = 6 + J4 的共轭是 $\overline { \textrm {z} }$ = 6 - J4,同样的,Z = -6 - J4 的共轭是 $\overline { \textrm {z} }$ = 6 + J4。
复数共轭的 Argand 图上的点在实轴上的水平位置与原始复数相同,但垂直位置相反。因此,复共轭可以被认为是复数的反射。以下示例显示复数 6 + j4 及其在复平面中的共轭。
共轭复数
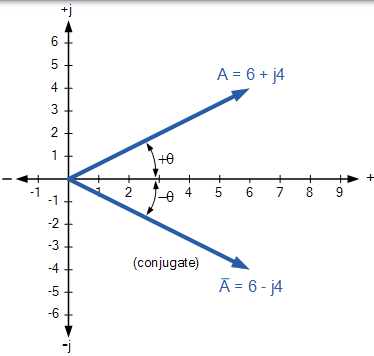
如上所述,复数与其复共轭的总和将始终为实数。然后,复数和其共轭的加法仅将结果作为实数或有效分量,而它们的减法仅给出虚数或无功分量。复数的共轭是电气工程中用于确定使用矩形形式的 AC 电路的视在功率的重要元件。
使用极坐标形式的复数
与绘制复平面中的点的矩形不同,复数的极坐标形式是根据其大小和角度来编写的。因此,极坐标形式向量表示为:Z =A∠±θ,其中: Z 是极坐标形式的复数,A 是向量的大小或模, θ 是 A 的角度,它可以是正的也可以是负的。该点的大小和角度仍然与上面的矩形形式相同,这次以极坐标形式,该点的位置以“三角形”表示,如下所示。
复数的极坐标表示
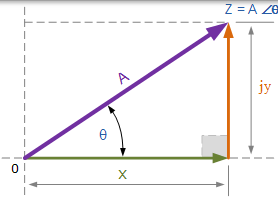
由于点的极坐标表示基于三角形,我们可以使用三角形的简单几何知识,特别是三角形和三角形的毕达哥拉斯定理来找到复数的大小和角度。正如我们从学校记得的那样,三角学处理三角形的边和角度之间的关系,因此我们可以将边之间的关系描述为:
$$ \begin{array} { l } { \mathrm { A } ^ { 2 } = \mathrm { x } ^ { 2 } + \mathrm { y } ^ { 2 } } \ { \mathrm { A } = \sqrt { \mathrm { x } ^ { 2 } + \mathrm { y } ^ { 2 } } } \end{array} $$
这里,$x = Acos \theta, y = Asin \theta$
再次使用三角学,A 的角度 θ 的可以求出来,
$$ \theta = \tan ^ { - 1 } \frac { \mathrm { y } } { \mathrm { x } } $$
然后在极坐标形式中,A 的长度及其角度而不是而不是点来表示复数。此外,在极坐标形式的复数的共轭具有相同的幅度或模,但角度的正负相反,所以示例 6∠30o 的共轭是 6∠-30o。
在矩形形式和极坐标形式之间转换
在矩形形式中,我们可以根据其直角坐标表示矢量,水平轴是其实轴,垂直轴是其虚轴或 j 分量。在极坐标形式中,这些实轴和虚轴简单地用 A∠θ 表示。然后使用上面的例子,矩形和极形之间的关系可以定义为。
将极坐标转换为矩形,(P→R)
$$ 6 \angle 30 ^ { \circ } = \mathrm { x } + \mathrm { jy } $$
但是,
$$ \mathrm { x } = \mathrm { A } \cos \theta \quad \mathrm { y } = \mathrm { A } \sin \theta $$
所以,
$$ \begin{aligned} 6 \angle 30 ^ { 0 } & = ( 6 \cos \theta ) + j ( 6 \sin \theta ) \\ & = \left( 6 \cos 30 ^ { \circ } \right) + j \left( 6 \sin 30 ^ { \circ } \right) \\ & = ( 6 \times 0.866 ) + j ( 6 \times 0.5 ) \\ & = 5.2 + j 3 \end{aligned} $$
我们还可以将矩形形式转换回极性形式,如下所示。
将矩形转换为极坐标形式,(R→P)
$$ ( 5.2 + j 3 ) = A \angle \theta $$
其中,
$$ A = \sqrt { 5.2 ^ { 2 } + 3 ^ { 2 } } = 6 \\ \theta = \tan ^ { - 1 } \frac { 3 } { 5.2 } = 30 ^ { \circ } $$
所以,
$$ ( 5.2 + j 3 ) = 6 \angle 30 ^ { 0 } $$
极坐标形式乘法和除法
如上所述,矩形形式最适合复数加法和减法,极坐标形式通常更适合乘法和除法。为了将极坐标形式的两个向量相乘,我们必须首先将两个模数或大小相乘,然后将它们的角度加在一起。
极坐标中的乘法
$$ Z _ { 1 } \times Z _ { 2 } = A _ { 1 } \times A _ { 2 } \angle \theta _ { 1 } + \theta _ { 2 } $$
6∠30o 和 8∠-45o 在极坐标下的乘法如下,
$$ Z _ { 1 } \times Z _ { 2 } = 6 \times 8 \angle 30 ^ { \circ } + \left( - 45 ^ { \circ } \right) = 48 \angle - 15 ^ { \circ } $$
极坐标除法
同样,为了将极坐标形式的两个矢量相除,我们必须将两个模数相除,然后减去它们的角度。
$$ \begin{array} { c } { \frac { Z _ { 1 } } { Z _ { 2 } } = \left( \frac { \mathrm { A } _ { 1 } } { \mathrm { A } _ { 2 } } \right) \angle \theta _ { 1 } - \theta _ { 2 } } \ { \frac { Z _ { 1 } } { Z _ { 2 } } = \left( \frac { 6 } { 8 } \right) \angle 30 ^ { \circ } - \left( - 45 ^ { 0 } \right) = 0.75 \angle 75 ^ { \circ } } \end{array} $$
幸运的是,今天的现代科学计算器已经建立了数学函数,可以很容易地将矩形转换成极坐标形式( R→P),然后从极坐标转换成矩形,( R→P)。
使用指数形式的复数
到目前为止,我们已经学习了矩形形式的复数 a + jb 和极坐标形式 A∠±θ,但是还有第三种表示复数的方法,它类似于对应于正弦曲线的长度(幅度)和相位角的极坐标形式,但使用自然对数的基数,e = 2.718 281 .. 来求复数的值。第三种方法称为指数形式。
指数形式使用正弦 sin 和余弦 cos 值来定义复指数为复平面上的旋转点。寻找点的位置的指数形式基于欧拉恒等式,以瑞士数学家 Leonhard Euler 的名字命名,具体如下:
$$ \begin{array} { c } { Z = A e ^ { j \phi } } \\ { Z = A ( \cos \phi + j \sin \phi ) } \end{array} $$
然后欧拉恒等式可以通过复平面中的以下旋转相量图来表示。
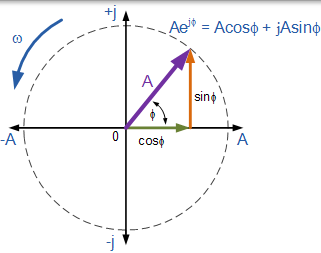
我们可以看到,欧拉公式是非常类似于上面的极坐标形式,一个数字,如 Aejθ ,它的幅值是 1,也是一个复数。我们不仅可以容易的将复数是的指数形式转换成极坐标形式,例如: 2 ej30 =2∠30,10 ej120 =10∠120 或 -6 ej90 =-6∠90,但欧拉恒等式也为我们提供了一种将复数从指数形式转换为矩形形式的方法。然后,定义复数的指数,极坐标和矩形之间的关系如下,
复数形式
$$ \mathrm { Z } = \mathrm { x } + \mathrm { jy } = \mathrm { A } \angle \theta = \mathrm { A } ( \cos \phi + j \sin \phi ) $$
相量表示法
到目前为止,我们已经研究了使用复数来表示复平面上的点的旋转矢量或静止矢量的不同方式。相量符号是构造具有给定正弦波形的幅度和相位角的单个复数的过程。
然后,有时称为相量符号或相量变换,将正弦函数的实部: A(t) = Am cos(ωt±Φ) 从时域转移到复数域,也称为频域。例如:
$$ \mathrm { V } _ { ( t ) } = \mathrm { V } _ { \mathrm { m } } \cos ( \omega \mathrm { t } + \theta ) \quad \Leftrightarrow \quad \text { Euler’sidentity: } \mathrm { e } ^ { \mathrm { t } \mathrm { j } \theta } = \cos \theta \pm \mathrm { j } \sin \theta \\ $$
举例如下,
$$ \mathrm { V } _ { ( \mathrm { t } ) } = 20 \cos \left( \omega \mathrm { t } + 30 ^ { \circ } \right) \mathrm { volts } \Rightarrow \left( \frac { 20 } { \sqrt { 2 } } \right) \angle 30 ^ { \circ } \Rightarrow \mathrm { V } _ { \mathrm { RMS } } = 14.14 \angle 30 ^ { \circ } \\ \mathrm { V } _ { ( \mathrm { t } ) } = 35 \cos \left( \omega \mathrm { t } + 45 ^ { \circ } \right) \mathrm { Volts } \Rightarrow \left( \frac { 35 } { \sqrt { 2 } } \right) \angle 45 ^ { \circ } \Rightarrow \mathrm { V } _ { \mathrm { RMS } } = 24.75 \angle 45 ^ { \circ } \\ \mathrm { V } _ { ( \mathrm { t } ) } = 35 \cos \left( \omega \mathrm { t } + 45 ^ { \circ } \right) \mathrm { Volts } \Rightarrow \left( \frac { 35 } { \sqrt { 2 } } \right) \angle 45 ^ { \circ } \Rightarrow \mathrm { V } _ { \mathrm { RMS } } = 24.75 \angle 45 ^ { \circ } \\ \mathrm { V } _ { ( \mathrm { t } ) } = 100 \cos ( \omega \mathrm { t } ) \text { Volts } \Rightarrow \left( \frac { 100 } { \sqrt { 2 } } \right) \angle 0 ^ { \circ } \Rightarrow \mathrm { V } _ { \mathrm { RMS } } = 70.72 \angle 0 ^ { \circ } $$
请注意, 1/√2 将最大幅值转换成有效值 或 RMS 值。
复数概述
然后总结本教程关于复数在电气工程中的使用。
- 复数由两个不同的数字组成,一个实数加上一个虚数。
- 通过使用 j 运算符将虚数与实数区分开来。
- 前面带有字母
j的数字将其标识为复平面中的虚数。 - 根据定义,j 算子 $j \equiv \sqrt { - 1 }$j≡√-1
- 虚数可以加,减,乘,除,这与实数相同。
j乘以j得到 j2 = -1- 在矩形形式中,复数由复平面上的空间中的点表示。
- 在极坐标形式中,复数由线表示,线的长度是幅度和相角。
- 在指数形式中,复数由线和相应的角度表示,该角度使用自然对数的基数。
- 复数可以用以下三种方式之一表示:
- Z = x + jy » 矩形
- Z =A∠Φ » 极坐标形式
- Z = AejΦ » 指数形式
- 欧拉恒等式可用于将复数从指数形式转换为矩形。
在之前的教程中,我们已经看到我们可以使用相量来表示正弦波形,并且它们的幅度和相位角可以以复数的形式写出。我们还看到复数可以以矩形、极坐标或指数形式呈现,每个复数代数形式之间的转换包括加,减,乘和除。
在接下来的几个与 AC 串联电路中相量关系相关的教程中,我们将研究一些常见无源电路元件的阻抗,并绘制流过元件的电流和施加电压的相量图。我们从 AC 阻抗开始。