交流电感和电感电抗

电流通过交流电感时的抵抗称为感应电抗，它取决于供电频率。

电感器和扼流圈基本上是线圈，它们缠绕在中空管（空心芯）上或缠绕在一些铁磁材料（铁芯）周围，以增加它们的感应值，这称为电感。

电感器以磁场的形式存储它们的能量，该磁场是在电感器的端子上施加电压时产生的。流过电感器的电流的增长不是瞬时的，而是由电感器自身的自感应或反电动势值决定的。然后对于电感线圈，该反电动势电压 VL 与流过它的电流的变化率成比例。

该电流将继续上升，直到达到其最大稳态状态，该状态大约为五个时间常数，此时该自感应反电动势已衰减为零。此时，稳态电流流过线圈，不再产生反电动势以抵抗电流，因此，线圈更像是一个短路，允许最大电流流过它。

然而，在包含 AC 电感的交流电路中，通过电感器的电流与稳态 DC 电压的行为非常不同。现在在交流电路中，流过线圈绕组的电流的抵抗不仅取决于线圈的电感，而且还取决于施加的电压波形的频率。

对流过 AC 电路中的线圈的电流的实际抵抗由线圈的 AC 电阻确定，该 AC 电阻由复数表示。但是为了区分 DC 电阻值和 AC 电阻值（也称为阻抗），使用术语电抗。

与电阻类似，电抗以欧姆为单位，但是用符号 X 来区别于纯电阻 R 值，并且因为所讨论的元件是电感器，电感器的电抗称为电感电抗 XL 以欧姆为单位。它的值可以从公式中找到。

感应电抗

$$ X _ { L } = 2 \pi f L $$

其中： XL 是以欧姆为单位的电感电抗， ƒ 是以赫兹为单位的频率，L 是线圈的电感，单位为 Henry。

我们还可以用弧度定义感抗，其中 ω 等于 2πf。

$$ X _ { L } = \omega L $$

因此，无论何时向电感线圈施加正弦电压，反电动势都会阻止流过线圈的电流的上升和下降，以及纯电感线圈，其电阻或损耗为零，此阻抗（可能是一个复数）等于其感应电抗。电抗也可以用矢量来表示，因为它具有幅度和方向（角度）。考虑下面的电路。

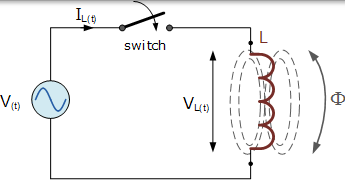
具有正弦电源的交流电感

此电路由一个 L 亨的纯电感的，横跨在以下表达式给出的正弦电压上连接： V(t) = VmaxsinωT。当开关闭合时，该正弦电压将导致电流流动并从零上升到其最大值。电流的这种上升或变化将在线圈内引起磁场，这反过来将抵抗或限制电流的这种变化。

但是，在电流有时间达到其在 DC 电路中的最大值之前，电压会改变极性，从而导致电流改变方向。在另一个方向上的这种变化再次被在线圈中的自感反电动势延迟。在只包含纯电感的电路中，电流被延迟 90o。

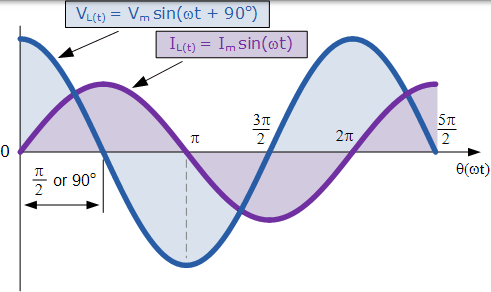
施加的电压在电流达到其最大正值之前的一个周期的四分之一（ 1 / 4f）内达到其最大正值，换句话说，施加到纯电感电路的电压将超前电流的四分之一周期或 90o，如下所示。

交流电感的正弦波形

这种效应也可以用相量图表示，在纯电感电路中电压超前电流 90o。但是，使用该电压作为我们的参考的话，我们也可以说，电流滞后于电压周期的四分之一或 90o，如示于下面的向量图。

交流电感的相量图

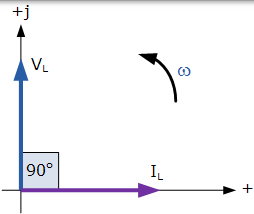
因此，对于纯粹的无损耗电感器，VL 超前 IL 90o，或者我们可以说 IL 滞后 VL 90o。

频率对感应电抗的影响

当一个 50Hz 的电源接在交流电感时，电流将有 90o 延迟，如先前所描述那样。并且在每个半周期结束电压反转极性之前，电流将达到峰值，即电流在 T 秒内达到最大值。

如果我们现在向线圈施加相同峰值电压的 100Hz 电源，电流仍将延迟 90o，但其最大值将低于 50Hz 时的值，因为频率增加所以达到其最大值所需的时间已减少，现在只有 1/2 T 秒达到其峰值。而且，由于频率的增加，线圈内的通量的变化率也增加。

然后根据上述感抗电抗等式，可以看出，如果频率或电感增加，则线圈的总感应电抗值也会增加。随着频率增加并接近无穷大，电感器电抗，因此其阻抗也会朝向无穷大增加，就像开路一样。

同样地，当频率接近零或 DC 时，电感器电抗也将减小到零，其作用类似于短路。这意味着感应电抗与频率成正比，并且在低频时具有较小值，在较高频率处具有较高值，如图所示。

感性电抗 vs 频率

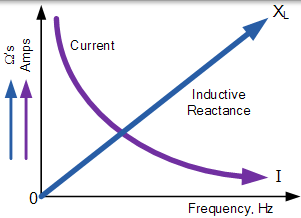
因此一个电感器的电抗随着其两端的频率增加而感抗增加。感抗与频率成正比（ XL ∝ ƒ），在电感器中产生的反电动势等于其电感乘以的电流变化的电感器中的速率。

此外，随着频率的增加，流过电感器的电流的值也会降低。

我们可以将非常低和非常高的频率对纯 AC 电感的电抗的影响表示如下：

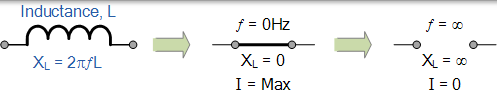
在包含纯电感的交流电路中，适用以下公式，

$$ \text { Current, I } = \frac { \text { Voltage } } { \text { Opposition to current flow } } = \frac { \mathrm { V } } { \mathrm { X } _ { \mathrm { L } } } $$

那么我们是如何得出这个等式的呢？ 电感中的自感电动势由法拉第定律确定，该法则由于电流的变化率而在电感器中产生自感应效应，并且感应电动势的最大值将对应于最大变化率。然后电感线圈中的电压如下：

$$ \mathrm { V } _ { \mathrm { L } ( \mathrm { t } ) } = \mathrm { L } \frac { \mathrm { di } _ { \mathrm { L } ( \mathrm { t } ) } } { \mathrm { dt } } $$

假如 $\mathrm { i } _ { \mathrm { L } ( \mathrm { t } ) } = \mathrm { I } _ { \max } \sin ( \omega \mathrm { t } )$ ，那么

$$ \begin{aligned} \mathrm { V } _ { \mathrm { L } ( t ) } & = \mathrm { L } \frac { \mathrm { d } } { \mathrm { dt } } \mathrm { I } _ { \max } \sin ( \omega \mathrm { t } + \theta ) \\ & = \omega \mathrm { L } \mathrm { I } _ { \max } \cos ( \omega \mathrm { t } + \theta ) \end{aligned} $$

那么交流电感两端的电压定义如下：

$$ \mathrm { V } _ { \mathrm { L } } = \omega \mathrm { L } \mathrm { I } _ { \max } \sin \left( \omega \mathrm { t } + 90 ^ { \circ } \right) $$

其中： VL =IωL，它是电压幅度， θ= + 90o，它是电压和电流之间的相位差或相位角。

相量域中

在相量域中，线圈两端的电压如下：

$$ \mathrm { V } _ { \mathrm { L } } = \mathrm { j } \omega \mathrm { L } \mathrm { I } $$

其中，$j \omega \mathrm { L } = \mathrm { j } \mathrm { X } _ { \mathrm { L } } = 2 \pi f \mathrm { L } = \mathrm { IMPED } \mathrm { ANCE } , \mathrm { Z }$

在极坐标形式，这可以写为： XL ∠90o 其中： $$ \mathrm { X } _ { \mathrm { L } } \angle \theta = \frac { \mathrm { V } _ { \mathrm { L } } \angle + 90 ^ { \circ } } { \mathrm { I } _ { \mathrm { L } } \angle 0 ^ { \circ } } $$

$$ \mathrm { X } _ { \mathrm { L } } \angle \theta = \mathrm { j } \omega \mathrm { L } = 0 + \mathrm { j } \mathrm { X } _ { \mathrm { L } } = \omega \mathrm { L } \angle + 90 ^ { \circ } = \mathrm { Z } \angle + 90 ^ { \circ } $$

串联 RL 电路的交流情况

我们已经看到，流经纯电感线圈的电流滞后电压 90o，当我们说纯电感线圈时，我们指的是没有欧姆电阻的电感，因此没有 I2 R 损耗。但在现实世界中，不可能只有纯粹的交流电感。

所有电气线圈、继电器、螺线管和变压器都将具有一定的电阻，无论与所使用的线圈匝数有多小。这是因为铜线具有电阻率。然后我们可以认为我们的感应线圈是一个由电阻 R 和 电感 L 串联组成，成为一个可以被称为“不纯电感”的电感线圈。

如果线圈具有一些“内部”电阻，那么我们需要将线圈的总阻抗表示为与电感串联的电阻。在包含电感 L 和电阻 R 的交流电路中，RL 的组合电压 V 是两个分量电压 VR 和 VL 的相量和。

这意味着流过线圈的电流仍将滞后于电压，但是取决于 VR 和 VL 的值，相量之和小于 90o。电压和电流波形之间的新角度给出了它们的相位差，正如我们所知，电路的相位角为 Φ。

考虑下面的电路是纯无感电阻 R 与纯电感 L 串联。

串联电阻 - 电感电路

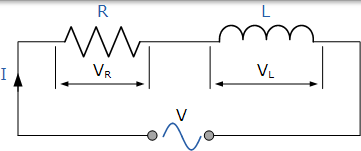
在上面的 RL 串联电路中，我们可以看到电流对电阻和电感都是共同的，而电压由两个分量电压 VR 和 VL 组成。可以通过数学方法或通过绘制矢量图找到这两个分量的最终电压。为了能够产生矢量图，必须找到参考变量，因为在串联 AC 电路中，相同的电流流过电阻和电感，所以电流是参考源。纯电阻和纯电感的单独矢量图如下：

两种纯元件的矢量图

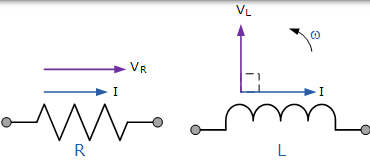
我们可以从上面和我们之前的关于交流电阻的教程中看到，电阻电路中的电压和电流都是同相的，因此矢量 VR 被叠加以绘制到电流矢量上。此外，从上述可知，电流滞后于（纯）交流电感电压，因此矢量 VL 画在在电流前面 90o，长度为 V-R 的相同比例，如图所示。

合成电压的矢量图

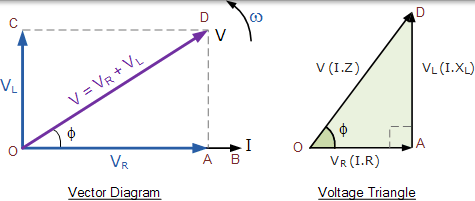
从上面的矢量图中，我们可以看到线 OB 是水平电流参考，线 OA 是电阻元件上与电流同相的电压。线 OC 表示在电流前 90o 的感应电压，因此仍然可以看出电流滞后纯电感电压 90o。线路 OD 为我们提供了最终的电源电压。然后：

• V 等于施加电压的有效值。
• I 等于串联电流的有效值。
• VR 等于电阻上的 IR 电压降，该电压与电流同相。
• VL 等于电感两端的 IXL 电压降，它超前电流 90o。

由于纯电感电流在正好滞后于电压 90o， 从单独的电压得出的所得相量图 VR 和 VL 代表如上所示的直角的三角形电压 OAD。然后我们也可以使用毕达哥拉斯定理在数学上找到电阻/电感（RL）电路上的合成电压值。

当 VR = IR 且 VL = IXL 时，所施加的电压将是两者的矢量和，如下：

$$ \begin{array} { c } { \mathrm { V } ^ { 2 } = \mathrm { V } _ { \mathrm { R } } ^ { 2 } + \mathrm { V } _ { \mathrm { L } } ^ { 2 } } \\ { \mathrm { V } = \sqrt { \mathrm { V } _ { \mathrm { R } } ^ { 2 } + \mathrm { V } _ { \mathrm { L } } ^ { 2 } } } \\ { \mathrm { V } = \sqrt { ( \mathrm { IR } ) ^ { 2 } + \left( \mathrm { I } . \mathrm { X } _ { \mathrm { L } } \right) ^ { 2 } } } \\ { \therefore \mathrm { I } = \frac { \mathrm { V } } { \sqrt { \mathrm { R } ^ { 2 } + \mathrm { X } _ { \mathrm { L } } ^ { 2 } } } } \end{array} $$

$\sqrt { \mathrm { R } ^ { 2 } + \mathrm { X } _ { \mathrm { L } } ^ { 2 } }$ 表示电路的阻抗 Z。

交流电感的阻抗

阻抗 Z 是对包含电阻（实部）和电抗（虚部）的交流电路中流动的电流的“全部”抵抗。阻抗也以欧姆 ω 作为单位。阻抗取决于电路的频率 ω，因为这会影响电路的无功元件，而在串联电路中，所有的电阻和无功阻抗都会加在一起。

阻抗也可以用复数表示，Z = R + jXL， 但它不是相量，它是两个或多个相量结合在一起的结果。如果我们将电压三角形的边上方除以 I，则得到另一个三角形，其边代表电路的电阻，电抗和阻抗，如下所示。

RL 阻抗三角形

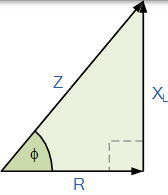
$$ \begin{array} { c } { Z = \frac { V } { I } } \\ { Z = \sqrt { R ^ { 2 } + X _ { L } ^ { 2 } } } \\ { \therefore Z ^ { 2 } = \left( R ^ { 2 } + X _ { L } ^ { 2 } \right) } \end{array} $$

阻抗2 = 电阻2 + （J 电抗)2， 其中 j 表示 90o 相移。

这意味着电压和电流之间的正相角 θ 为。

相位角

$$ \begin{aligned} \mathrm { Z } ^ { 2 } & = \mathrm { R } ^ { 2 } + \mathrm { X } _ { \mathrm { L } } ^ { 2 } \\ \cos ^ { - 1 } \phi & = \frac { \mathrm { R } } { \mathrm { Z } } \\ \sin ^ { - 1 } \phi & = \frac { \mathrm { X } _ { \mathrm { L } } } { \mathrm { Z } } \\ \tan ^ { - 1 } \phi & = \frac { \mathrm { X } _ { \mathrm { L } } } { \mathrm { R } } \end{aligned} $$

虽然我们上面的例子代表了一个简单的非纯交流电感，但如果两个或多个感应线圈串联在一起，或者一个线圈与许多无感电阻串联，那么电阻元件的总电阻将相等至： R1 + R2 + R3 等，这样求出电路的总电阻值。

同样，电感元件的总电抗等于：X1 + X2 + X3 等，求出电路的总电抗值。这样，包含许多扼流圈，线圈和电阻器的电路可以容易地求出单个阻抗值 Z，它由与等效的单个电阻串联单个等效电感，Z2 = R2 + X2。

交流电感实例 No1

在下面的电路中，电源电压定义为： V(t) = 230 sin(314t - 30o) ，L = 2.2H。确定流过线圈的电流值并绘制得到的相量图。

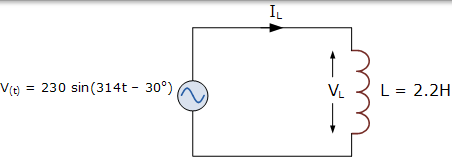
线圈两端的电压与电源电压相同。将此时域值转换为极坐标形式可得出： VL = 230∠-30o V。线圈的感抗是： XL = ωL = 314×2.2 = 690 Ω。然后使用欧姆定律找到流过线圈的电流：

$$ \mathrm { I } _ { \mathrm { L } } = \frac { \mathrm { V } _ { \mathrm { L } } } { \mathrm { j } \mathrm { X } _ { \mathrm { L } } } = \frac { 230 \angle - 30 ^ { \circ } } { 690 } \angle 90 ^ { \circ } = 0.33 \angle 120 ^ { \circ } ( \mathrm { A } ) $$

结合电流滞后于电压 90o， 相量图如下，

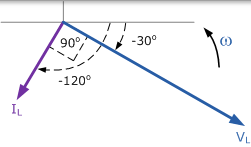
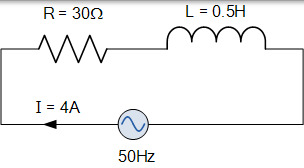
交流电感实例 No2

线圈的电阻为 30Ω，电感为 0.5H。如果流过线圈的电流是 4 安培，频率为 50Hz，电源电压的值是多少？

电路的阻抗将是：

$$ \begin{aligned} \mathrm { X } _ { \mathrm { L } } & = 2 \pi f \mathrm { L } = 2 \pi \times 50 \times 0.5 = 157 \Omega \\ \mathrm { Z } & = \sqrt { \mathrm { R } ^ { 2 } + \mathrm { X } _ { \mathrm { L } } ^ { 2 } } \\ \mathrm { Z } & = \sqrt { 30 ^ { 2 } + 157 ^ { 2 } } \\ \mathrm { Z } & = 159.8 \Omega \end{aligned} $$

然后，每个元件的电压降计算如下：

$$ \begin{array} { l } { \mathrm { V } _ { \mathrm { S } } = \mathrm { I.Z } = 4 \times 159.8 = 640 \mathrm { v } } \\ { \mathrm { V } _ { \mathrm { R } } = \mathrm { I.R } = 4 \times 30 = 120 \mathrm { v } } \\ { \mathrm { V } _ { \mathrm { L } } = \mathrm { I.X } _ { \mathrm { L } } = 4 \times 157 = 628 \mathrm { v } } \end{array} $$

电流和电源电压之间的相角计算如下：

$$ \tan ^ { - 1 } \phi = \frac { \mathrm { X } _ { \mathrm { L } } } { \mathrm { R } } = \frac { 157 } { 30 } = 79.2 ^ { \circ } $$

相量图将是。

在下一个关于交流电容的教程中，我们将看一下电容器的稳压状态正弦交流波形的电压 - 电流关系，以及纯电容和非纯电容的相量图表示。