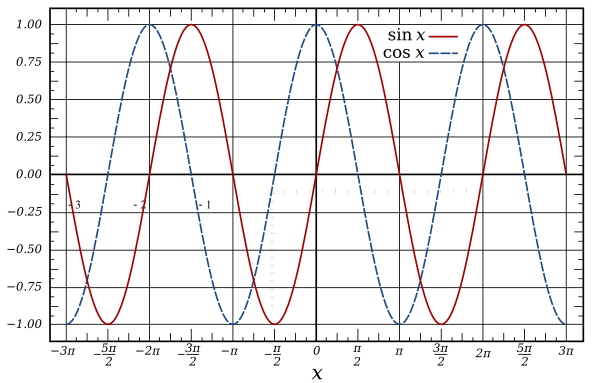
使用 Math.sin 的周期函数

Math.sin 和 Math.cos 是循环的，周期为 2 * PI 弧度（360 度），它们输出幅度为 2 的波，范围为 -1 到 1。

正弦和余弦函数图:( 维基百科提供）

它们对于许多类型的周期性计算都非常方便，从创建声波到动画，甚至编码和解码图像数据

此示例显示如何创建一个简单的正弦波，控制周期/频率，相位，幅度和偏移。

使用的时间单位是秒。
最简单的形式，仅控制频率。

// time is the time in seconds when you want to get a sample
// Frequency represents the number of oscillations per second
function oscillator(time, frequency){  
    return Math.sin(time * 2 * Math.PI * frequency);
}

几乎在所有情况下，你都希望对返回的值进行一些更改。修改的常用术语

• 相位：从振荡开始的频率偏移。它是一个 0 到 1 范围内的值，其中值 0.5 将波向前移动一半的频率。值 0 或 1 不做任何更改。
• 幅度：一个周期内距最低值和最高值的距离。幅度为 1 的范围为 2.最低点（波谷）-1 至最高（峰值）1。对于频率为 1 的波峰值为 0.25 秒，波谷为 0.75。
• 偏移：向上或向下移动整个波。

要在函数中包含所有这些：

function oscillator(time, frequency = 1, amplitude = 1, phase = 0, offset = 0){
    var t = time * frequency * Math.PI * 2; // get phase at time
    t += phase * Math.PI * 2; // add the phase offset
    var v = Math.sin(t); // get the value at the calculated position in the cycle
    v *= amplitude; // set the amplitude
    v += offset; // add the offset
    return v;
}

或者以更紧凑（并且更快的形式）：

function oscillator(time, frequency = 1, amplitude = 1, phase = 0, offset = 0){
    return Math.sin(time * frequency * Math.PI * 2 + phase * Math.PI * 2) * amplitude + offset; 
}

除时间之外的所有论据都是可选的