狀態變數濾波器

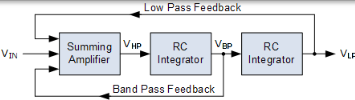
狀態變數濾波器是一種多路反饋濾波電路，可以同時從同一個單個有源濾波器設計中產生所有三個濾波器響應，低通，高通和帶通。

狀態可變濾波器使用三個（或更多）運算放大器電路（有源元件）級聯在一起以產生單獨的濾波器輸出，但如果需要，還可以新增額外的求和放大器以產生第四個陷波濾波器輸出響應。

狀態可變濾波器是二階 RC 有源濾波器，由兩個相同的運算放大器積分器組成，每個積分器用作一階單極點低通濾波器，一個求和放大器，我們可以在其周圍設定濾波器增益及其阻尼反饋網路。來自所有三個運算放大器級的輸出訊號反饋到輸入，允許我們定義電路的狀態。

一個狀態變數濾波器設計的主要優點是，所有三個濾波器主要引數，增益（ A ），角頻率，ƒC 和濾波器 Q 可以在不影響濾波器效能獨立設定。

事實上，如果設計正確，低通幅度響應和高通幅度響應的 -3dB 截止頻率（ ƒc ）應與帶通級的中心頻率點相同。即 ƒLP（-3dB） 等於 ƒHP（-3dB） 等於 ƒBP(center)。此外，帶通濾波器響應的阻尼因子（ ζ ）應等於 1 / Q，因為 Q 將設定為-3dB (0.7071)。

雖然濾波器提供低通（LP），高通（HP）和帶通（BP）輸出，但這種濾波器電路的主要應用是作為狀態可變帶通濾波器設計，其中心頻率由兩個 RC 整數設定。

雖然我們之前已經看到帶通濾波器的特性可以通過簡單地將低通濾波器與高通濾波器級聯在一起獲得，但狀態可變帶通濾波器的優勢在於它們可以被調諧為高選擇性（高 Q）提供中心頻率點的高增益。

有幾種狀態可變濾波器設計可用，所有這些都基於標準濾波器設計，可提供反相和非反相變化。但是，基本濾波器設計對於兩種變化都是相同的，如下面的框圖表示所示。

狀態變數濾波器框圖

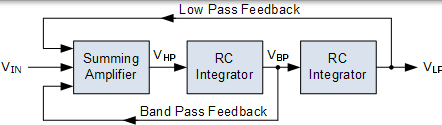
然後我們可以從上面的基本框圖中看到，狀態變數濾波器有三個可能的輸出，VHP，VBP 和 VLP，每個輸出來自三個運算放大器。通過增加第四個運算放大器也可以實現陷波濾波器響應。

在恆定輸入電壓下，求和放大器輸出的 VIN 產生高通響應，該響應也成為第一個 RC 積分器的輸入。該積分器的輸出產生帶通響應，該響應成為第二個 RC 積分器的輸入，在其輸出端產生低通響應。結果，可以找到關於輸入電壓的每個單獨輸出的單獨傳遞函式。

因此，基本的非反相狀態變數濾波器設計如下：

狀態可變濾波器電路

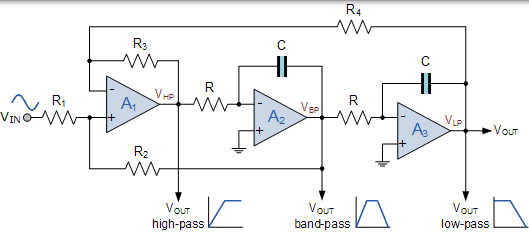
並且狀態變數濾波器的三個輸出的幅度響應將如下所示：

狀態變數濾波器的歸一化響應

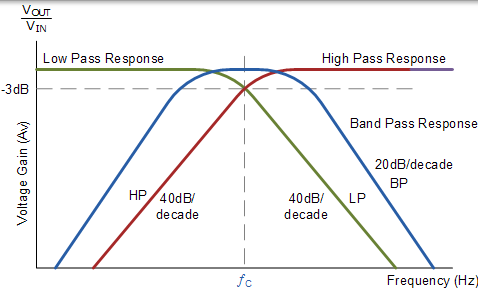
狀態變數濾波器的主要設計元素之一是使用兩個運算放大器積分器。正如我們在積分器教程中看到的那樣，運算放大器整合器在其反饋環路中使用電容形式的頻率相關阻抗。當使用電容器時，輸出電壓與輸入電壓的積分成比例，如圖所示。

運算放大器積體電路

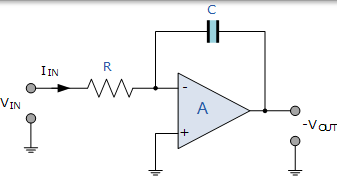
$$ \mathrm { V } _ { \mathrm { OUT } } = - \frac { 1 } { \mathrm { R } \mathrm { C } } \int _ { 0 } ^ { \mathrm { t } } \mathrm { V } _ { \mathrm { IN } } \mathrm { dt } $$ 為了簡化數學運算，還可以在頻域中重寫為：

輸出電壓 Vout 是輸入電壓 Vin 相對於時間的積分的常數 1/RC 倍。積分器產生相位滯後，負號（ - ）表示 180° 相移，因為輸入訊號直接連線到運算放大器的反相輸入端。

在上述運算放大器 A2 的情況下，其輸入訊號連線到前一個運算放大器 A1 的輸出，因此其輸入為 VHP，輸出為 VBP。然後從上面，運算放大器 A2 的表示式可以寫成：

然後通過重新排列該公式，我們可以找到反相積分器 A2 的傳遞函式。

運算放大器 A2 傳遞函式

$$ \frac { \mathrm { V } _ { \mathrm { OUT } } } { \mathrm { V } _ { \mathrm { IN } } } = \frac { \mathrm { V } _ { \mathrm { BP } } } { \mathrm { V } _ { \mathrm { HP } } } = - \frac { 1 } { 2 \pi f _ { \mathrm { C } } \mathrm { RC } } $$

基於完全相同的假設，我們可以找到另一個運算放大器積分器 A3 的傳遞函式

運算放大器 A3 傳遞函式

$$ \frac { \mathrm { V } _ { \mathrm { OUT } } } { \mathrm { V } _ { \mathrm { IN } } } = \frac { V _ { \mathrm { LP } } } { V _ { \mathrm { BP } } } = - \frac { 1 } { 2 \pi f _ { \mathrm { C } } \mathrm { RC } } $$

因此，兩個運算放大器積分器 A2 和 A3 以級聯方式連線在一起，因此第一個（ VBP ）的輸出成為第二個輸入。因此我們可以看到帶通響應是通過積分高通響應產生的，低通響應是通過積分帶通響應產生的。因此，VHP 和 VLP 之間的傳遞函式如下：

$$ \frac { V _ { L P } } { V _ { H P } } = - \frac { 1 } { 2 \pi f _ { C } R C } \times - \frac { 1 } { 2 \pi f _ { C } R C } = \frac { 1 } { \left( 2 \pi f _ { c } R C \right) ^ { 2 } } $$

注意，每個積分器級提供反相輸出，因為它們是反相積分器，但總和輸出將為正。如果使用完全相同的 R 和 C 值使得兩個電路具有相同的積分器時間常數，則可以將兩個放大器電路視為具有截止頻率 fC 的單個積分器電路。

與兩個積分器電路一樣，濾波器還具有差分求和放大器，提供其輸入的加權求和。這裡的優點是，求和放大器 A1 的輸入將振盪反饋，阻尼和輸入訊號組合到濾波器，因為所有三個輸出都被反饋到求和輸入。

放大器求和電路

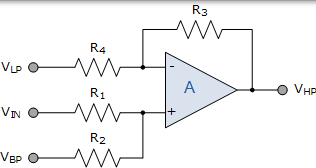
運算放大器 A1 連線為加法器 - 減法器電路。也就是說，它將輸入訊號 VIN 與運算放大器 A2 的 VBP 輸出相加，並從運算放大器 A3 的 VLP 輸出中減去，因此：

$$ \mathrm { i } _ { 1 } = \frac { \mathrm { V } _ { \mathrm { IN } } - ( + \mathrm { V } ) } { \mathrm { R } _ { 1 } } + \frac { ( + \mathrm { V } ) - \mathrm { V } _ { \mathrm { BP } } } { \mathrm { R } _ { 2 } } = 0 $$

所以，

$$ \begin{array} { l } { \mathrm { V } _ { \mathrm { IN } } \mathrm { R } _ { 2 } = + \mathrm { V } \left( \mathrm { R } _ { 1 } + \mathrm { R } _ { 2 } \right) - \mathrm { V } _ { \mathrm { BP } } \mathrm { R } _ { 1 } } \ { \therefore \quad + \mathrm { V } = \frac { \mathrm { V } _ { \mathrm { IN } } \mathrm { R } _ { 2 } + \mathrm { V } _ { \mathrm { BP } } \mathrm { R } _ { 1 } } { \left( \mathrm { R } _ { 1 } + \mathrm { R } _ { 2 } \right) } } \end{array} $$

和

$$ \mathrm { i } _ { 2 } = \frac { \mathrm { V } _ { \mathrm { HP } } - ( - \mathrm { V } ) } { \mathrm { R } _ { 3 } } + \frac { ( - \mathrm { V } ) - \mathrm { V } _ { \mathrm { LP } } } { \mathrm { R } _ { 4 } } = 0 $$

所以，

$$ \begin{array} { l } { \mathrm { V } _ { \mathrm { HP } } \mathrm { R } _ { 4 } = - \mathrm { V } \left( \mathrm { R } _ { 3 } + \mathrm { R } _ { 4 } \right) - \mathrm { V } _ { \mathrm { LP } } \mathrm { R } _ { 3 } } \ { \therefore \quad - \mathrm { V } = \frac { \mathrm { V } _ { \mathrm { LP } } \mathrm { R } _ { 3 } + \mathrm { V } _ { \mathrm { HP } } \mathrm { R } _ { 4 } } { \left( \mathrm { R } _ { 3 } + \mathrm { R } _ { 4 } \right) } } \end{array} $$

作為差分輸入，運算放大器的 +V 和 -V 是相同的，即： +V - -V，我們可以重新排列上面的兩個表示式，找到 A1 輸出的傳遞函式，即高通輸出。 $$ \frac { \mathrm { V } _ { \mathrm { IN } } \mathrm { R } _ { 2 } + \mathrm { V } _ { \mathrm { BP } } \mathrm { R } _ { 1 } } { \left( \mathrm { R } _ { 1 } + \mathrm { R } _ { 2 } \right) } = \frac { \mathrm { V } _ { \mathrm { LP } } \mathrm { R } _ { 3 } + \mathrm { V } _ { \mathrm { HP } } \mathrm { R } _ { 4 } } { \left( \mathrm { R } _ { 3 } + \mathrm { R } _ { 4 } \right) } $$

因此，

$$ \begin{array} { l } { \left( \mathrm { V } _ { \mathrm { IN } } \mathrm { R } _ { 2 } + \mathrm { V } _ { \mathrm { BP } } \mathrm { R } _ { 1 } \right) \left( \mathrm { R } _ { 3 } + \mathrm { R } _ { 4 } \right) = \left( \mathrm { V } _ { \mathrm { LP } } \mathrm { R } _ { 3 } + \mathrm { V } _ { \mathrm { HP } } \mathrm { R } _ { 4 } \right) \left( \mathrm { R } _ { 1 } + \mathrm { R } _ { 2 } \right) } \ { \mathrm { V } _ { \mathrm { IM } } \mathrm { R } _ { 2 } \left( \mathrm { R } _ { 3 } + \mathrm { R } _ { 4 } \right) + \mathrm { V } _ { \mathrm { BP } } \mathrm { R } _ { 1 } \left( \mathrm { R } _ { 3 } + \mathrm { R } _ { 4 } \right) = \mathrm { V } _ { \mathrm { LP } } \mathrm { R } _ { 3 } \left( \mathrm { R } _ { 1 } + \mathrm { R } _ { 2 } \right) + \mathrm { V } _ { \mathrm { Hp } } \mathrm { R } _ { 4 } \left( \mathrm { R } _ { 1 } + \mathrm { R } _ { 2 } \right) } \end{array} $$

重新排列輸出為，

$$ \mathrm { V } _ { \mathrm { HP } } = \mathrm { V } _ { \mathrm { IN } } \frac { \mathrm { R } _ { 2 } \left( \mathrm { R } _ { 3 } + \mathrm { R } _ { 4 } \right) } { \mathrm { R } _ { 3 } \left( \mathrm { R } _ { 1 } + \mathrm { R } _ { 2 } \right) } + \mathrm { V } _ { \mathrm { BP } } \frac { \mathrm { R } _ { 1 } \left( \mathrm { R } _ { 3 } + \mathrm { R } _ { 4 } \right) } { \mathrm { R } _ { 4 } \left( \mathrm { R } _ { 1 } + \mathrm { R } _ { 2 } \right) } - \mathrm { V } _ { \mathrm { LP } } \frac { \mathrm { R } _ { 3 } \left( \mathrm { R } _ { 1 } + \mathrm { R } _ { 2 } \right) } { \mathrm { R } _ { 4 } \left( \mathrm { R } _ { 1 } + \mathrm { R } _ { 2 } \right) } \\ \therefore \mathrm { V } _ { \mathrm { HP } } = \mathrm { V } _ { \mathrm { IN } } \frac { \mathrm { R } _ { 2 } \left( \mathrm { R } _ { 3 } + \mathrm { R } _ { 4 } \right) } { \mathrm { R } _ { 3 } \left( \mathrm { R } _ { 1 } + \mathrm { R } _ { 2 } \right) } + \mathrm { V } _ { \mathrm { BP } } \frac { \mathrm { R } _ { 1 } \left( \mathrm { R } _ { 3 } + \mathrm { R } _ { 4 } \right) } { \mathrm { R } _ { 4 } \left( \mathrm { R } _ { 1 } + \mathrm { R } _ { 2 } \right) } - \mathrm { V } _ { \mathrm { LP } } \frac { \mathrm { R } _ { 3 } } { \mathrm { R } _ { 4 } } $$

我們從上面知道，VBP 和 VLP 分別是兩個積分器 A2 和 A3 的輸出。通過將 A2 和 A3 的積分器方程代入上述方程，我們得到狀態變數濾波器的傳遞函式為：

狀態可變濾波器傳遞函式

$$ \frac { \mathrm { V } _ { \mathrm { ouT } } } { \mathrm { V } _ { \mathrm { IN } } } = \frac { \mathrm { V } _ { \mathrm { LP } } } { \mathrm { V } _ { \mathrm { II } } } = \frac { \frac { \mathrm { R } _ { 2 } \left( \mathrm { R } _ { 3 } + \mathrm { R } _ { 4 } \right) } { \mathrm { R } _ { 3 } \left( \mathrm { R } _ { 1 } + \mathrm { R } _ { 2 } \right) } \times \left( \frac { 1 } { \mathrm { RC } } \right) } { \frac { \mathrm { R } _ { 3 } \left( \mathrm { R } _ { 3 } + \mathrm { R } _ { 4 } \right) } { \mathrm { R } _ { 4 } \left( \mathrm { R } _ { 1 } + \mathrm { R } _ { 2 } \right) } \times \frac { 1 } { 2 \pi f \mathrm { RC } } ) + \left( \frac { 1 } { 2 \pi f \mathrm { RC } } \right) ^ { 2 } } $$

我們之前說過狀態可變濾波器產生三個濾波器響應，低通，高通和帶通，並且帶通響應是非常窄的高 Q 濾波器的響應，這在上面的狀態變數濾波器傳遞函式中很明顯，因為它類似於標準的二階響應。

歸一化的二階傳遞函式

$$ \frac { \mathrm { V } _ { \mathrm { OUT } } } { \mathrm { V } _ { \mathrm { IN } } } = \frac { \mathrm { A } _ { 0 } \left( \frac { f } { f _ { \mathrm { o } } } \right) } { \left[ 1 + 2 \xi \frac { f } { f _ { \mathrm { o } } } + \left( \frac { f } { f _ { \mathrm { o } } } \right) ^ { 2 } \right] } $$

濾波器轉折頻率，ƒC

如果我們使積分器輸入電阻器和反饋電容器相同，那麼狀態變數濾波器截止頻率可以很容易地調整而不會影響其整體 Q 值。同樣，可以在不改變截止頻率的情況下改變 Q 的值。然後截止頻率為：

狀態可變濾波器截止頻率

$$ 2 \pi f _ { C } = \sqrt { \frac { R _ { 3 } } { R _ { 4 } ( R C ) ^ { 2 } } } \quad \therefore f _ { C } = \sqrt { \frac { R _ { 3 } } { R _ { 4 } ( 2 \pi R C ) ^ { 2 } } } $$

如果我們使反饋電阻 R3 和 R4 的值相同，則狀態變數濾波器的每個濾波器輸出的截止頻率變為：

$$ f _ { C ( H P ) } = f _ { C ( B P ) } = f _ { C ( L P ) } = \frac { 1 } { 2 \pi R C } $$

然後，簡單地通過改變電阻器 R 或電容器 C 來完成狀態變數截止頻率的調諧。

狀態變數濾波器的特徵不僅在於它們各自的輸出響應，還在於濾波器質量因子 Q。Q 涉及帶通濾波器幅度響應曲線的“銳度”，Q 越高，輸出響應越高或越尖銳，導致濾波器具有高選擇性。

對於帶通濾波器，Q 被定義為中心頻率除以濾波器 -3dB 頻寬，即 Q =ƒc/ BW。但是 Q 也可以從上述傳遞函式的分母中找到，因為它是阻尼因子（ ζ ） 的倒數。那麼 Q 如下所示：

狀態變數濾波器的 Q 因子

$$ Q = \frac { f _ { C } } { B W } = \frac { 1 } { 2 \zeta } = \frac { R _ { 1 } \left( R _ { 3 } + R _ { 4 } \right) } { R _ { 4 } \left( R _ { 1 } + R _ { 2 } \right) } \sqrt { \frac { R _ { 3 } } { R _ { 4 } } \times \frac { R C } { R C } } $$

再次，如果電阻器 R3 和 R4 是相等的並且積分分量 R 和 C 是相等的，那麼最終平方根表達會降低到： √1 也就是 1，因為分子和分母相互抵消。

狀態變數濾波器示例 No1

設計一種狀態變數濾波器，其具有截止頻率 ƒC 為 1kHz 和品質因數 Q 為 10。假設兩個頻率確定電阻和電容是相等的。確定濾波器 DC 增益並繪製得到的電路和波特圖。

我們在上面說過，如果兩個積分電路的電阻，R 和反饋電容 C 都是相同的值，即 R = R 和 C = C，則濾波器的截止或截止頻率點簡單給出如：

濾波器的截止頻率

$$ f _ { C } = \frac { 1 } { 2 \pi R C } H z $$

我們可以選擇電阻器或電容器的值來找到另一個的值。如果我們為電容器假設一個合適的 10nF 值，那麼電阻器的值將是：

$$ R = \frac { 1 } { 2 \pi f _ { C } C } = \frac { 1 } { 2 \pi \times 1000 \times 10 n F } = 15.9 k \Omega $$ 給出 C = 10nF 和 R =15.9kΩ，或最接近的優選值 16kΩ 。

值 Q 被給定為 10。這與濾波器阻尼係數有關：

$$ Q = 10 = \frac { 1 } { 2 \zeta } \quad \therefore 2 \zeta = \frac { 1 } { 10 } = 0.1 $$ 在上面的狀態變數傳遞函式中，2ζ 部分被電阻器組合代替，給出：

$$ 2 \zeta = \frac { 1 } { Q } = \frac { 1 } { 10 } = \frac { R _ { 1 } \left( R _ { 3 } + R _ { 4 } \right) } { R _ { 4 } \left( R _ { 1 } + R _ { 2 } \right) } \sqrt { \frac { R _ { 3 } } { R _ { 4 } } \times \frac { R C } { R C } } = 0.1 $$ 我們從上面知道 R =16kΩ 且 C = 10nF，但如果我們假設兩個反饋電阻 R3 和 R4 相同並且等於 10kΩ，那麼上面的等式減少到：

$$ 0.1 = \frac { R _ { 1 } \left( R _ { 3 } + R _ { 4 } \right) } { R _ { 4 } \left( R _ { 1 } + R _ { 2 } \right) } = \frac { R _ { 1 } ( 10 k \Omega + 10 k \Omega ) } { 10 k \Omega \left( R _ { 1 } + R _ { 2 } \right) } $$

假設輸入電阻的值 R1 為 1kΩ，那麼我們可以找到 R2 的值如下：

$$ \therefore \mathrm { R } _ { 2 } = \frac { \mathrm { R } _ { 1 } \left( \mathrm { R } _ { 3 } + \mathrm { R } _ { 4 } \right) } { 0.1 \times \mathrm { R } _ { 4 } } - \mathrm { R } _ { 1 } \\ = \frac { 1 \mathrm { k } \Omega ( 10 \mathrm { k } \Omega + 10 \mathrm { k } \Omega ) } { 0.1 \times 10 \mathrm { k } \Omega } - \mathrm { IkS } = 19 \mathrm { k } \Omega $$

從上面的歸一化傳遞函式，DC 通帶增益定義為 Ao， 並且從等效狀態變數濾波器傳遞函式，這相當於：

SVF 濾波器直流通帶增益

$$ \begin{array} { l } { A _ { O } = \frac { R _ { 2 } \left( R _ { 3 } + R _ { 4 } \right) } { R _ { 3 } \left( R _ { 1 } + R _ { 2 } \right) } = \frac { 19 k \Omega ( 10 k \Omega + 10 k \Omega ) } { 10 k \Omega ( 1 k \Omega + 19 k \Omega ) } } \ { \therefore A _ { 0 } = 1.9 = 5.57 \mathrm { dB } } \end{array} $$

因此，濾波器的直流電壓增益計算為 1.9，基本上等於 R2 / R3。另外，濾波器的最大增益 ƒC ：可以計算為 Ao ×Q，如下所示。

SVF 濾波器最大增益

$$ \begin{array} { c } { A _ { f _ { c } ) } = \frac { V _ { O \cup T } } { V _ { I N } } = \frac { A _ { O } } { 2 \zeta } = A _ { O } \times Q } \ { \therefore A _ { 0 } \times Q = 1.9 \times 10 = 19 = 25.6 \mathrm { d } B } \end{array} $$

狀態可變濾波器電路

然後，狀態可變濾波器電路的設計將是： R =16kΩ，C = 10nF，R1 =1kΩ，R2 =19kΩ，R3 = R4 =10kΩ，如圖所示。

狀態變數濾波器設計

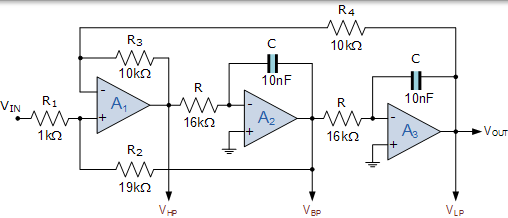
現在我們可以在 1 到 1MHz 的頻率範圍內將狀態可變濾波器電路的各個輸出響應曲線繪製到波特圖上，如圖所示。

狀態可變濾波器波特圖

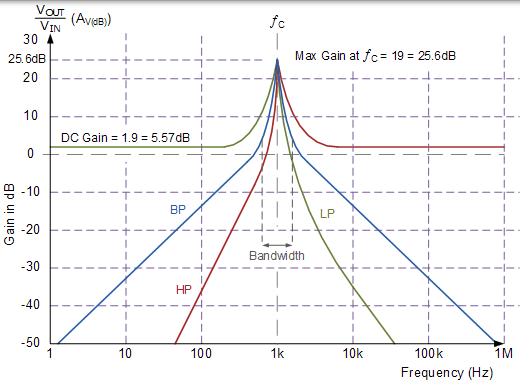
然後我們可以從上面的濾波器響應曲線看出，濾波器電路的 DC 增益為 5.57dB，相當於如上所計算的開環電壓增益 Ao 為 1.9。響應還表明，由於 Q 的值，輸出曲線在拐角頻率處的最大電壓增益達到峰值 25.6dB。作為 Q 還涉及帶通濾波器中心頻率，以它的頻寬，濾波器的頻寬將因此： ƒo / 10 = 100Hz。

我們已經在這個狀態變數濾波器教程中看到，我們可以使用多反饋技術從同一個單獨的啟用中同時產生所有三個濾波器響應，低通，高通和帶通，而不是產生一種頻率響應的有源濾波器。

但是除了三個基本濾波器響應之外，我們還可以在上面的基本狀態變數濾波器設計中新增一個額外的運算放大器電路，以產生類似於標準陷波濾波器的第四個輸出響應。

陷波濾波器設計

陷波濾波器濾波基本上是一個帶通濾波器的相反，因為它拒絕或停止頻率的特定頻帶。然後陷波濾波器也稱為“帶阻濾波器”。為了從基本狀態可變濾波器設計中獲得陷波濾波器的響應，我們必須使用另一個運算放大器求和放大器 A4 將高通和低通輸出響應相加，如圖所示。

陷波濾波器電路

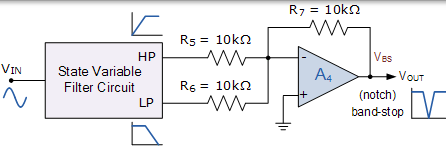
這裡簡單起見，我們假設這兩個輸入電阻 R5 和 R6 以及反饋電阻 R7 都具有相同的值 10kΩ，R3 和 R4 也相同。因此，這使陷波濾波器的增益為 1。

陷波濾波器和帶通濾波器的輸出響應與帶通響應的中心頻率相關，等於陷波濾波器的零響應點，並且在該示例中將是 1kHz。

此外，陷波的頻寬由電路 Q 確定，與通帶響應完全相同。因此，向下的峰值等於中心頻率除以 -3dB 頻寬，即陷波兩側 -3dB 點之間的頻率差。注意，品質因數 Q 與凹口的實際深度無關。

這種基本的陷波濾波器（帶阻）設計只有兩個輸入應用於其求和放大器，即低通輸出，VLP 和高通輸出 VHP。但是，我們還有兩個可用於基本狀態可變濾波器電路的訊號，帶通輸出，VBP 和輸入訊號本身 VIN。

如果這兩個訊號中的一個也用作陷波濾波器求和放大器的輸入以及低通和高通訊號，則可以控制陷波的深度。

根據你想要如何控制陷波濾波器部分的輸出，將取決於你將使用的兩個可用訊號中的哪一個。如果它被要求從在無阻尼固有頻率的積極響應的否定響應輸出缺口變化 ƒo 然後帶通輸出訊號 VBP 將被使用。

同樣，如果要求輸出陷波僅在其向下的負深度變化，則將使用輸入訊號 VIN。如果通過可變電阻器將這兩個附加訊號中的任何一個連線到運算放大器求和放大器，則可以完全控制陷波的深度和方向。考慮下面修改的陷波濾波器電路。

可變陷波濾波器深度

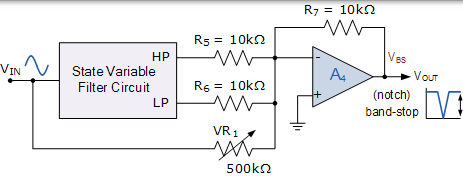
狀態變數濾波器摘要

狀態變數濾波器電路是二階有源 RC 濾波器設計使用多個反饋技術以產生三個不同的頻率響應的輸出，即：低通，高通和帶通從相同的單個濾波器。狀態變數濾波器優於其他基本濾波器設計的優點是可以獨立調整三個主要濾波器引數 Gain，Q 和 ƒc。

我們在這裡也看到濾波器也很容易調整，因為截止頻率 ƒc 可以通過改變 R 或 C 來設定和調整，而不會影響濾波器的阻尼係數。但是，在較高的截止頻率和較大的阻尼係數下，濾波器會變得不穩定，因此最好在低 Q 值，小於 10 和低截止頻率下使用。

基本狀態可變濾波器設計使用三個運算放大器部分來產生其輸出，但我們也看到，增加了第四個運算放大器部分，將低通和高通部分相加，一個陷波（帶阻）濾波器輸出響應也可以在所需的中心頻率下實現。