無源高通濾波器

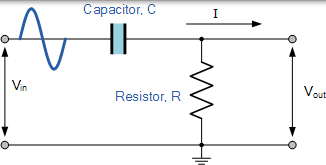
高通濾波器與低通濾波器電路完全相反，因為兩個元件已經互換，濾波器輸出訊號現在從電阻器中得到。

其中作為低通濾波器只允許低於其截止頻率 ƒc 的訊號通過，無源高通濾波器電路正如其名稱所暗示的，僅通過所選擇的分界點 ƒc 以上的訊號，從而濾除了任何低頻訊號波形。考慮下面的電路。

高通濾波器電路

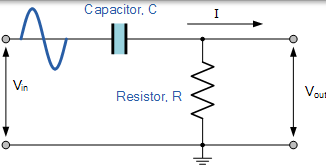
在這種電路中，電容器的電抗在低頻時非常高，因此電容器的作用類似於開路，並且在 VIN 處阻止任何輸入訊號，直到達到截止頻率點 fC。在該截止頻率點以上，電容器的電抗已經充分降低，現在更像是短路，允許所有輸入訊號直接傳遞到輸出，如下面濾波器響應曲線所示。

一階高通濾波器的頻率響應

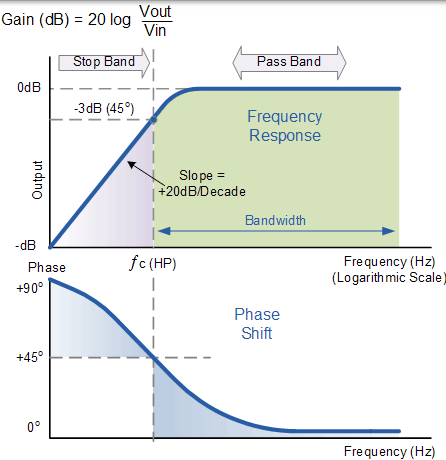
上面的無源高通濾波器的波特圖或頻率響應曲線與低通濾波器的波特圖或頻率響應曲線完全相反。這裡訊號在低頻衰減，輸出以 +20dB / Decade（6dB / Octave）的斜率上升，直到頻率達到截止點（ ƒc ），這裡 R = Xc。它的響應從無限低延申至截止頻率，其中輸出電壓幅度是輸入訊號值的 1 /√2 = 70.7% 的或輸入的 -3dB（20 log (Vout/Vin)）。

此外，我們可以看出，輸出訊號的相位角 Φ 超前 輸入，在頻率 ƒc 處等於 45o。此濾波器的頻率響應曲線意味著濾波器可以將傳遞到直無窮大的所有訊號。然而，在實際中，濾波器響應不會延伸到無窮大，而是受所用元件的電氣特性的限制。

可以使用與低通濾波器相同的等式找到一階高通濾波器的截止頻率點，但是相移的公式稍微修改了下，以適應正相移的情況，如下所示。

截止頻率和相移

$$ \begin{array} { l } { f c = \frac { 1 } { 2 \pi R C } } \\ { \text { Phase Shift } \phi = \arctan \frac { 1 } { 2 \pi f R C } } \end{array} $$

電路增益 Av 以 Vout / Vin（幅度）給出，計算公式如下：

$$ A _ { v } = \frac { V _ { O U T } } { V _ { I N } } = \frac { R } { \sqrt { R ^ { 2 } + X c ^ { 2 } } } = \frac { R } { Z } $$

在低頻處，$\mathrm { Xc } \rightarrow \infty , ) Vout ( = 0$

在高頻處，$\mathrm { Xc } \rightarrow 0 , ) Vout ( = \mathrm { Vin }$

高通濾波器示例 No1

計算一個簡單的無源高通濾波器的截止頻率 ƒc，該濾波器由一個與 240kΩ 電阻串聯的 82pF 電容組成。

$$ f c = \frac { 1 } { 2 \pi R C } = \frac { 1 } { 2 \pi \times 240,000 \times 82 \times 10 ^ { - 12 } } = 8,087 H z \text { or } 8 k H z $$

二階高通濾波器

與低通濾波器一樣，高通濾波器級可以級聯在一起以形成如圖所示的二階（兩極）濾波器。

二階高通濾波器

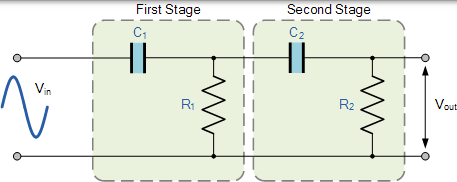
上述電路使用兩個一階濾波器連線或級聯在一起形成二階或兩極高通網路。然後，通過簡單地使用額外的 RC 網路，可以將一階濾波器級轉換為二階型別，與二 階低通濾波器的道理相同。得到的二階高通濾波器電路的斜率為 40dB / decade（12dB /octave）。

與低通濾波器一樣，截止頻率 ƒc 由電阻器和電容器決定，如下所示。

$$ f _ { \mathrm { C } } = \frac { 1 } { 2 \pi \sqrt { \mathrm { R } _ { 1 } \mathrm { C } _ { 1 } \mathrm { R } _ { 2 } \mathrm { C } _ { 2 } } } \mathrm { Hz } $$

高通濾波器摘要

我們已經看到無源高通濾波器與低通濾波器完全相反。該濾波器沒有 DC(0Hz) 的輸出電壓，直到指定的截止頻率 ƒc 點。截止頻率點是允許通過的電壓增益的 70.7% 或 -3dB （dB = -20log VOUT / VIN ）。

截止點 ƒc 以下的頻率範圍通常稱為阻帶，而“高於”該截止點的頻率範圍通常稱為通帶。

使用標準公式： ƒc= 1 /(2πRC) 可以找到高通濾波器的截止頻率，轉角頻率或 -3dB 點。在所得到的輸出訊號的相位角 ƒc 是 45o。通常，由於較高的工作頻率，高通濾波器比其等效低通濾波器的失真更小。

這種型別的無源濾波器的一個非常常見的應用是在音訊放大器中作為兩個音訊放大器級之間的耦合電容器和揚聲器系統，以將較高頻率的訊號引導到較小的“高音揚聲器”型揚聲器，同時阻擋較低的低音訊號或者是也用作濾波器以減少任何低頻噪聲或“隆隆”型失真。當在音訊應用中這樣使用時，高通濾波器有時被稱為“低切”或“低音切割”濾波器。

如前所述，輸出電壓 Vout 取決於時間常數和輸入訊號的頻率。將 AC 正弦訊號應用於電路時，它表現為簡單的一階高通濾波器。但是，如果我們將輸入訊號改變為具有幾乎垂直階躍輸入的“方波”形訊號，則電路的響應會發生顯著變化併產生通常稱為微分器的電路。

RC 微分器

到目前為止，濾波器的輸入波形被假定為正弦波或由基波訊號和在頻域中工作的一些諧波組成的正弦波的輸入波形，給出了濾波器的頻域響應。但是，如果我們使用在時域中工作的方波訊號為高通濾波器提供脈衝或階躍響應輸入，則輸出波形將由短持續時間脈衝或尖峰組成，如圖所示。

RC 微分電路

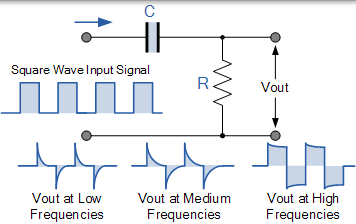
方波輸入波形的每個週期在輸出端產生兩個尖峰，一個正極和一個負極，其幅度等於輸入的幅度。尖峰的衰減速率取決於兩個分量的時間常數 RC 值 (t = RC) 和輸入頻率的值。隨著頻率的增加，輸出脈衝越來越像輸入訊號的形狀。