有源帶通濾波器

帶通濾波器或任何濾波器的主要特徵是它能夠在指定頻帶或被稱為“通帶”的頻率範圍內傳遞相對無衰減的頻率。

對於低通濾波器，該通帶從 0Hz 或 DC 開始，並繼續向上到指定的截止頻率點，距離最大通帶增益 -3dB。同樣，對於高通濾波器，通帶從 -3dB 截止頻率開始，並繼續向無窮大或有源濾波器的最大開環增益。

然而，有源帶通濾波器略有不同，因為它是一種用於電子系統的頻率選擇濾波器電路，用於分離一個特定頻率的訊號，或一系列位於特定“頻帶”頻率範圍內的訊號。該頻帶或頻率範圍設定在標記為“下截止低頻率”（ fL ）和“上截止頻率”（ fH ）的兩個截止頻率之間，同時衰減這兩個點之外的任何訊號。

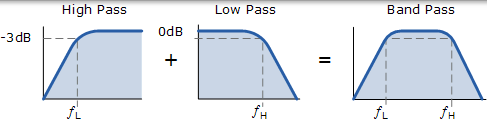
如圖所示，通過將單個低通濾波器與單個高通濾波器級聯在一起，可以輕鬆實現簡單的有源帶通濾波器。

低通濾波器（LPF）的截止頻率高於高通濾波器（HPF）的截止頻率，-3dB 點的頻率差異將決定“低頻濾波器”的“頻寬”。帶通濾波器，同時衰減這些點之外的任何訊號。製作簡單的有源帶通濾波器的一種方法是將我們先前看到的基本無源高通和低通濾波器連線到放大運算放大器電路，如圖所示。

有源帶通濾波器電路

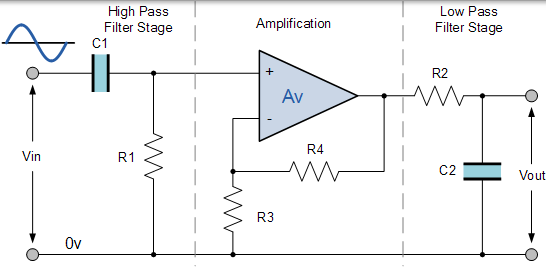
將低通和高通濾波器級聯在一起產生低“Q 因子”型濾波器電路，其具有寬通帶。濾波器的第一級將是高通級，使用電容器阻止來自源的任何 DC 偏置。該設計具有產生相對平坦的不對稱通帶頻率響應的優點，其中一半表示低通響應，另一半表示高通響應，如圖所示。

高截止頻率（ ƒH ）以及低截止頻率（ ƒL ）用同以前一樣在標準的一階低通和高通濾波器電路的方法來計算。顯然，在兩個截止點之間需要合理的分離，以防止低通和高通階段之間的任何相互作用。放大器還提供兩級之間的隔離，並定義電路的整體電壓增益。

因此，濾波器的頻寬是這兩個高低 -3dB 點之間的差值。例如，假設我們有一個帶通濾波器，其 -3dB 截止點設定為 200Hz 和 600Hz。然後濾波器的頻寬將給出為：頻寬（BW）= 600-200 = 400Hz。

有源帶通濾波器的歸一化頻率響應和相移如下。

有源帶通頻率響應

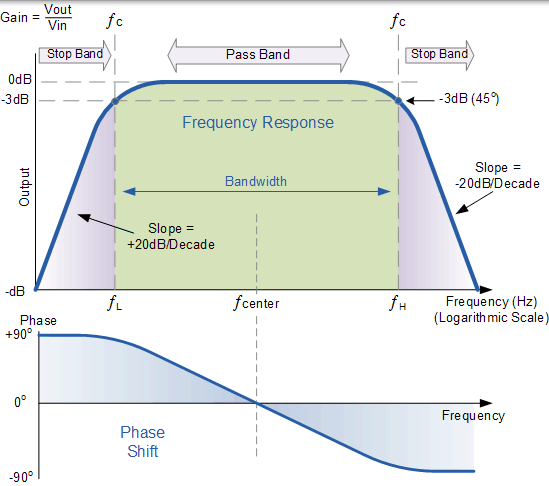
雖然上述無源調諧濾波器電路將用作帶通濾波器，但通帶（頻寬）可能非常寬，如果我們想要隔離一小段頻率，這可能是一個問題。有源帶通濾波器也可以使用反相運算放大器製成。

因此，通過重新排列濾波器內電阻器和電容器的位置，我們可以產生更好的濾波器電路，如下所示。用於有源帶通濾波器，該下截止 -3dB 點由 ƒC1 表示，而上截止 -3dB 點由 ƒC2 表示。

反相帶通濾波器電路

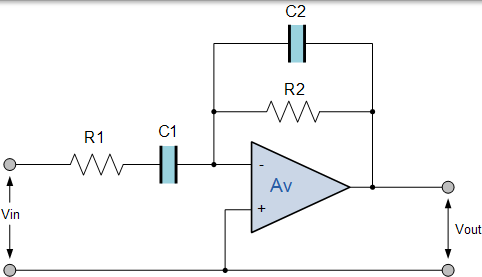
$$ \text { Voltage Gain } = - \frac { R _ { 2 } } { R _ { 1 } } , \quad f _ { C _ { 1 } } = \frac { 1 } { 2 \pi R _ { 1 } C _ { 1 } } , f c _ { 2 } = \frac { 1 } { 2 \pi R _ { 2 } C _ { 2 } } $$

這種型別的帶通濾波器設計為具有更窄的通帶。濾波器的中心頻率和頻寬與 R1，R2，C1 和 C2 的值相關。濾波器的輸出取自運算放大器的輸出。

多反饋帶通有源濾波器

我們可以通過重新排列元件來改善上述電路的帶通響應，以產生無限增益多反饋（IGMF）帶通濾波器。這種型別的有源帶通設計產生一個基於負反饋有源濾波器的“調諧”電路，使其具有高“Q 因子”（高達 25）的幅度響應和在其中心頻率兩側的急劇滾降。因為電路的頻率響應類似於諧振電路，所以該中心頻率被稱為諧振頻率（ ƒr ）。考慮下面的電路。

無限增益多反饋有源濾波器

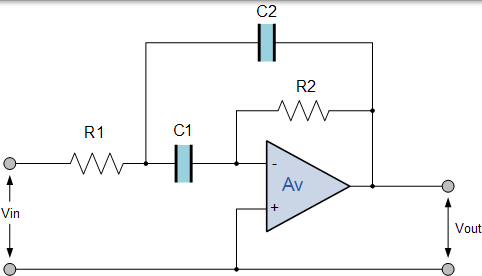
該有源帶通濾波器電路使用運算放大器的全增益，通過電阻器 R2 和電容器 C2 施加多個負反饋。然後我們可以定義 IGMF 濾波器的特徵如下：

$$ f _ { \mathrm { r } } = \frac { 1 } { 2 \pi \sqrt { \mathrm { R } _ { 1 } \mathrm { R } _ { 2 } \mathrm { C } _ { 1 } \mathrm { C } _ { 2 } } } \quad \mathrm { Q } _ { \mathrm { BP } } = \frac { f _ { \mathrm { r } } } { \mathrm { BW } _ { ( 3 \mathrm { d } \mathrm { B } ) } } = \frac { 1 } { 2 } \sqrt { \frac { \mathrm { R } _ { 2 } } { \mathrm { R } _ { 1 } } } $$

最大增益，$ \mathrm { A } \mathrm { v } = - \frac { \mathrm { R } _ { 2 } } { 2 \mathrm { R } _ { 1 } } = - 2 \mathrm { Q } ^ { 2 }$

我們可以看到電阻器 R1 和 R2 之間的關係決定了帶通“Q 因子”和最大幅度出現的頻率，電路的增益將等於 -2Q2。然後隨著增益的增加，選擇性也隨之增加。換句話說，高增益 - 高選擇性。

有源帶通濾波器示例 No1

具有電壓增益 Av 為 1 和 1kHz 的諧振頻率 ƒr 的有源帶通濾波器是有無限增益多反饋濾波器電路來搭建的。計算實現電路所需的元件值。

首先，我們可以使用電路的增益確定有源濾波器所需的兩個電阻 R1 和 R2 的值，如下所示。

$$ \mathrm { Av } = 1 = - 2 \mathrm { Q } ^ { 2 } \quad \therefore \mathrm { Q } _ { \mathrm { BP } } = \sqrt { \frac { 1 } { 2 } } = 0.7071 \\ Q = 0.7071 = \frac { 1 } { 2 } \sqrt { \frac { R _ { 2 } } { R _ { 1 } } } \quad \therefore \frac { R _ { 2 } } { R _ { 1 } } = \left( \frac { 0.7071 } { \frac { 1 } { 2 } } \right) ^ { 2 } = 2 $$

然後我們可以看到 Q = 0.7071 的值給出了電阻器的關係，R2 是電阻器 R1 的兩倍。然後我們可以選擇任何合適的電阻阻值來給出所需的比率 2，比如電阻 R1 =10kΩ，R2 =20kΩ。

中心或諧振頻率為 1kHz。使用獲得的新電阻值，我們可以確定所需的電容值，假設 C = C1 = C2。

$$ \begin{array} { c } { f _ { \mathrm { r } } = 1,000 \mathrm { Hz } = \frac { 1 } { 2 \pi \mathrm { C } \sqrt { \mathrm { R } _ { 1 } \mathrm { R } _ { 2 } } } } \ { \therefore \mathrm { C } = \frac { 1 } { 2 \pi f _ { \mathrm { r } } \sqrt { \mathrm { R } _ { 1 } \mathrm { R } _ { 2 } } } = \frac { 1 } { 2 \pi 1000 \sqrt { 10,000 \times 20,000 } } = 11.2 \mathrm { nF } } \end{array} $$

最接近的標準值是 10nF。

諧振頻率點

任何無源或有源帶通濾波器的頻率響應曲線的實際形狀將取決於濾波器電路的特性，上面的曲線被定義為“理想”帶通響應。有源帶通濾波器是二階型濾波器，因為它的電路設計中有兩個無功分量（兩個電容）。

由於這兩個無功分量，濾波器將在其“中心頻率” ƒc 處具有峰值響應或諧振頻率 ƒr。中心頻率通常計算為上下截止點之間的兩個 -3dB 頻率的幾何平均值，諧振頻率（振盪點）如下：

$$ f_{r} = \sqrt { f _ { L } \times f _ { H } } $$

其中，

• ƒR 是諧振或中心頻率
• ƒL 是 -3dB 的下截止頻率
• ƒH 是 -3db 的上截止頻率

在上面簡單的例子中，濾波器的 -3dB 截止點分別位於 200Hz 和 600Hz，那麼有源帶通濾波器的諧振中心頻率將為：

$$ f r = \sqrt { 200 \times 600 } = \sqrt { 120,000 } = 346 \textrm{ Hz} $$

Q-Factor 或品質因數

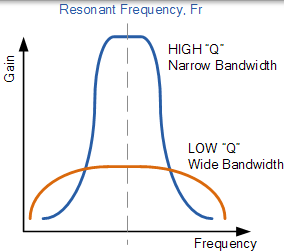
在帶通濾波器電路中，濾波器的上下 -3dB 截止頻率之間的實際通帶的總寬度決定了電路的品質因數 - Quality Factor。Q 因子衡量帶通濾波器對於給定的頻率擴充套件的“選擇性”或“非選擇性”。Q 因子的值越低，濾波器的頻寬越寬，因此 Q 因子越高，濾波器越窄，“選擇性”越強。

濾波器的Q 因子 有時用希臘符號 α 代表，並且被稱為 α 峰值頻率，其中：

$$ \alpha = \frac { 1 } { Q } $$

由於有源帶通濾波器（二階系統）的品質因數與濾波器響應在其中心諧振頻率（ ƒr ） 附近的“銳度”有關，因此它也可以被認為是“阻尼係數”。因為濾波器的阻尼越大，其響應越平坦，同樣，濾波器的阻尼越小，其響應越敏銳。阻尼比用希臘符號 ξ 表示。其中，

$$ \xi = \frac { \alpha } { 2 } $$

帶通濾波器的 Q 是上下 -3dB 頻率之間的諧振頻率 （ ƒr ）與頻寬 （ BW ） 之比，如下所示：

$$ Q = \frac { \text { Resonant Frequency } } { \text { Bandwidth } } $$

然後，對於上面的簡單示例，帶通濾波器的品質因數“ Q ”如下所示：

346Hz / 400Hz = 0.865。請注意，Q 是比率，沒有單位。

在分析有源濾波器時，通常考慮歸一化電路，其產生具有矩形形狀的“理想”頻率響應，以及通帶和具有非常陡峭的滾降斜率的阻帶之間的過渡。然而，這些理想的響應在現實世界中是不可能的，因此我們使用近似值來為我們設計的濾波器型別提供最佳頻率響應。

可能最著名的近似濾波器是 Butterworth 或最大平坦響應濾波器。在下一個教程中，我們將研究更高階的濾波器，並使用巴特沃斯近似來產生濾波器，在通帶中其頻率響應與數學理論上一樣平坦，並具有平滑的過渡或滾降速率。