巴特沃斯滤波器设计
在之前的滤波器教程中,我们研究了简单的一阶型低通和高通滤波器,它们的 RC 滤波器电路设计中只包含一个电阻器和一个无功元件(电容器)。
在使用滤波器对信号的频谱进行整形的应用中,例如在通信或控制系统中,滚降的形状或宽度也称为“过渡带”,对于简单的一阶滤波器可能太长,所以有源的滤波器需要具有多阶滤波器。这些类型的滤波器通常被称为“高阶”或“n阶”滤波器。
滤波器复杂度或滤波器类型由滤波器阶数决定,并且取决于其设计中的电抗器或电感器等无功元件的数量。我们还知道,滚降速率和过渡频带的宽度取决于滤波器的阶数和简单的一阶滤波器的标准滚降速率为 20dB / decade 或 6dB/octave。
然后,对于具有 n 阶滤波的滤波器,它相应的将具有 20n dB/decade 或 6n dB/Octave 的滚降率。因此,一阶滤波器的滚降速率为 20dB / decade(6dB/octave),二阶滤波器的滚降速率为 40dB / decade(12dB/octave),四阶滤波器的滚降率为 80dB / decade(24dB / octave)等。
通常通过将单个一阶滤波器和二阶滤波器级联在一起来形成诸如三阶,四阶和五阶的高阶滤波器。
例如,两个二阶低通滤波器可以级联在一起以产生四阶低通滤波器,依此类推。尽管可以形成的滤波器的顺序没有限制,但随着顺序的增加,其尺寸和成本也增加,其精度也会下降。
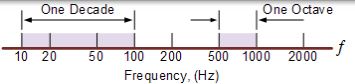
Decade 和 Octave
关于Decade 和 Octave 的最后评论。在频率范围内,Decase 是十倍增长(乘以 10)或十倍减少(除以 10)。例如,2 至 20Hz 一个 decade,而 50 至 5000Hz 代表 2 个 decade(50 至 500Hz,然后 500 至 5000Hz)。
一个 Octave 是在频率标度的加倍(乘以 2)或减半(除以 2)。例如,10 到 20Hz 表示一个 octave,而 2 到 16Hz 是三个 octave(2 到 4,4 到 8,最后是 8 到 16Hz),每次加倍频率。无论哪种方式,在使用放大器和滤波器时,对数在频域中广泛用于表示频率值,因此理解它们非常重要。
对数频率标度
由于频率确定电阻器均相等,且可如频率确定电容,截止或转角频率( ƒC 为)或者第一,第二,第三或甚至第四阶滤波器也必须相等,并且可以使用我们现在已经熟悉的等式:
$$ f _ { C } = \frac { 1 } { 2 \pi R C } H z $$
与第一和第二阶滤波器一样,通过简单地交换等效低通滤波器中的频率确定元件(电阻器和电容器)的位置来形成第三和第四阶高通滤波器。可以按照我们之前在低通滤波器和高通滤波器教程中看到的步骤设计高阶滤波器。然而,高阶滤波器的总增益是固定的,因为所有频率确定分量都相等。
滤波近似值
到目前为止,我们已经研究了低通和高通一阶滤波器电路,它们产生的频率和相位响应。一个理想的滤波器将为我们提供最大通带增益和平坦度,最小阻带衰减以及阻止频带滚降(转换频带)的非常陡峭的通带,因此显然会有大量的网络响应满足这些要求。
毫不奇怪,线性模拟滤波器设计中有许多“近似函数”,它们使用数学方法来最好地逼近滤波器设计所需的传递函数。
这种设计被称为 Elliptical,Butterworth,Chebyshev,Bessel,Cauer 以及许多其他设计。在这五个“经典”线性模拟滤波器近似函数中,只有巴特沃斯滤波器,特别是低通巴特沃斯滤波器设计在这里被认为是最常用的功能。
低通巴特沃斯滤波器设计
巴特沃斯滤波器近似函数的频率响应通常也被称为“最大平坦”(无波纹)响应,因为通带被设计为具有频率响应,该频率响应在数学上可能从 0Hz(DC) 直到截止频率-3dB 处无波纹。超过截止点的较高频率在阻带中以 20dB / decade 或 6dB/octave 下降至零。这是因为的“品质因数” Q 仅为 0.707。
然而,巴特沃斯滤波器的一个主要缺点是,当滤波器从通带变为阻带时,它以宽的过渡带为代价实现了该通带平坦度。它也具有差的相位特性。对于不同的滤波器阶数,理想的频率响应和标准巴特沃斯近似值如下所示。
巴特沃斯滤波器的理想频率响应
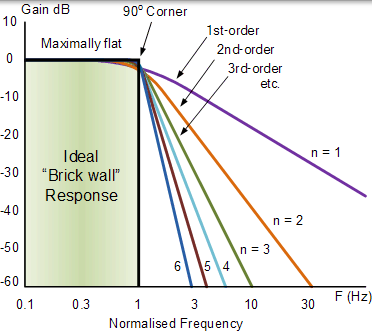
请注意,巴特沃斯滤波器阶数越高,滤波器设计中的级联级数越高,滤波器越接近理想的“砖墙”响应。
然而,在实践中,巴特沃斯的理想频率响应是无法实现的,因为它会产生过多的通带纹波。
在表示 N 阶 Butterworth 滤波器的广义等式中,频率响应如下:
$$ \left| H _ { ( j \omega ) } \right| = \frac { 1 } { \sqrt { 1 + \varepsilon ^ { 2 } \left( \frac { \omega } { \omega _ { p } } \right) ^ { 2 n } } } $$
其中: N 表示滤波器阶数,ω 等于 2πƒ 和 ε 是最大通带增益 Amax。如果 Amax 被定义为截止频率 -3dB ƒc 的频率,ε 将会等于一个,因此 ε2 也将会是 1。但是,如果你现在希望定义 Amax 在不同的电压增益值,例如 1 dB 或 1.1220(1dB = 20 * logAmax )之后,ε 的新值 可通过以下方式计算,
$$ H _ { 1 } = \frac { H _ { 0 } } { \sqrt { 1 + \varepsilon ^ { 2 } } } $$
其中,
- H0 是通带最大增益 Amax
- H1 是通带最小增益
转换等式给出:
$$ \frac { H _ { 0 } } { H _ { 1 } } = 1.1220 = \sqrt { 1 + \varepsilon ^ { 2 } } $$
然后会得出
$$ \varepsilon = 0.5088 $$
滤波器的频率响应可以通过其传递函数在数学上定义,标准电压传递函数 H(jω) 写为:
$$ H ( j \omega ) = \left[ \frac { V o u t ( j \omega ) } { V i n ( j \omega ) } \right] $$
其中,
- Vout = 输出信号电压。
- Vin = 输入信号电压。
- j = -1的平方根(√-1)
- ω = 弧度频率(2πƒ)
注意: (jω) 也可以写成 (s) 来表示 s 域。二阶低通滤波器的合成传递函数如下:
$$ H ( s ) = \frac { V o u t } { V i n } = \frac { 1 } { S ^ { 2 } + S + 1 } $$
归一化低通巴特沃斯滤波器多项式
为了帮助来设计低通滤波器,Butterworth 生成了归一化二阶低通多项式的标准表,给出了系数值,该值对应于 1 弧度/秒的截止转角频率。
| N | 因子形式的归一化分母多项式 |
|---|---|
| 1 | (1 + s) |
| 2 | (1 + 1.414s + s2 ) |
| 3 | (1 + s)(1 + s + s2 ) |
| 4 | (1 + 0.765s + s2 )(1 + 1.848s + s2 ) |
| 五 | (1 + s)(1 + 0.618s + s2 )(1 + 1.618s + s2 ) |
| 6 | (1 + 0.518s + s2 )(1 + 1.414s + s2 )(1 + 1.932s + s2 ) |
| 7 | (1 + s)(1 + 0.445s + s2 )(1 + 1.247s + s2 )(1 + 1.802s + s2 ) |
| 8 | (1 + 0.390s + s2 )(1 + 1.111s + s2 )(1 + 1.663s + s2 )(1 + 1.962s + s2 ) |
| 9 | (1 + s)(1 + 0.347s + s2 )(1 + s + s2 )(1 + 1.532s + s2 )(1 + 1.879s + s2 ) |
| 10 | (1 + 0.313s + s2 )(1 + 0.908s + s2 )(1 + 1.414s + s2 )(1 + 1.782s + s2 )(1 + 1.975s + s2 ) |
滤波器设计 - 低通巴特沃斯滤波器
求出有源低通巴特沃兹滤波器的阶数,其规格如下:在通带频率 ωp 200 rad/s (31.8 Hz) 的 Amax = 0.5dB,阻带频率 ωs 800 rad/s 下 Amin = -20dB。设计合适的巴特沃斯滤波器电路以满足这些要求。
首先,最大通带增益 Amax = 0.5dB,等于增益 1.0593,记住:0.5dB = 20 * log(A),频率( ωp )为 200 rad/s,所以 ε 为:
$$ \begin{array} { l } { 1.0593 = \sqrt { 1 + \varepsilon ^ { 2 } } } \\ { \therefore \varepsilon = 0.3495 \quad } \\ \varepsilon ^ { 2 } = 0.1221 \end{array} $$
其次,最小阻带增益 Amin = -20dB,其等于在 800 rads / s 或 127.3Hz 的阻带频率( ωs )下的增益 10 (-20dB = 20 * log(A))。
将这些值代入 Butterworth 滤波器频率响应的一般方程式,可以得到以下结果: $$ H ( j \omega ) = \frac { H _ { 0 } } { \sqrt { 1 + \varepsilon ^ { 2 } \left( \frac { \omega _ { S } } { \omega _ { p } } \right) ^ { 2 n } } } \\ \frac { 1 } { 10 } = \frac { 1 } { \sqrt { 1 + 0.1221 \left( \frac { 800 } { 200 } \right) ^ { 2 n } } } \\ ( 10 ) ^ { 2 } = 1 + 0.1221 \times 4 ^ { 2 n } \\ \therefore 100 - 1 = 0.1221 \times 4 ^ { 2 n } \\ 4 ^ { 2 n } = \frac { 99 } { 0.1221 } = 810.811 \\ 4 ^ { n } = \sqrt { 810.811 } = 28.475 \\ \therefore n = \frac { \log 28.475 } { \log 4 } = 2.42 $$
由于 n 必须始终为整数(整数),因此 2.42 下一个整数值为 n = 3,因此需要三阶滤波器并生成三阶巴特沃斯滤波器,二阶滤波器阶段需要与一阶滤波器级联级联。
从上面的归一化低通巴特沃斯多项式表中,三阶滤波器的系数为 (1 + s)(1 + s + s2 ),这给出了 3-A = 1 的增益,或 A = 2。当 A = 1 +(Rf / R1)时,为反馈电阻器 Rf 和电阻器 R1 选择分别为 1kΩ 和 1kΩ 的值 - (1kΩ/1kΩ) + 1 = 2。
我们知道,截止拐角频率 ωo 可以使用公式 1/CR 来计算 ,但我们需要从通带频率 ωp 找到 ωo。
$$ \begin{array} { c } { | H ( j \omega ) | = \frac { H _ { 0 } } { \sqrt { 1 + \varepsilon ^ { 2 } \left( \frac { \omega _ { 0 } } { \omega _ { p } } \right) ^ { 2 n } } } } \\ { 3 d B = 1.414 \text { at } \omega = \omega _ { 0 } } \\ \frac { 1 } { 1.414 } = \frac { 1 } { \sqrt { 1 + \varepsilon ^ { 2 } \left( \frac { \omega _ { 0 } } { \omega _ { p } } \right) ^ { 2 n } } } \\ 2 = 1 + \varepsilon ^ { 2 } \left( \frac { \omega _ { 0 } } { \omega _ { P } } \right) ^ { 2 n } \\ \therefore 1 = \varepsilon \left( \frac { \omega _ { 0 } } { \omega _ { P } } \right) ^ { n } \\ \omega _ { 0 } ^ { n } = \frac { \omega _ { P } ^ { n } } { \varepsilon } \\ \omega _ { 0 } ^ { 3 } = \frac { 200 ^ { 3 } } { 0.3495 } \\ \omega _ { 0 } ^ { 3 } = 22.889 \times 10 ^ { 6 } \\ \therefore \omega _ { O } = 283.93 = 284 \text { rads } / s \end{array} $$
因此,截止频率为 284 rads / s 或 45.2Hz(284 /2π),使用熟悉的公式 1 / CR,我们可以找到三阶电路的电阻和电容值。
$$ \begin{array} { l } { 284 r a d s / s = \frac { 1 } { C R } \text { use a value of } R = 10 k \Omega } \ { \therefore \text { Capacitor } C = \frac { 1 } { 284 \times 10,000 } = 0.352 u F } \end{array} $$
注意,最接近 0.352uF 的优选值是 0.36uF,或 360nF。
三阶巴特沃斯低通滤波器
最后我们的三阶低通巴特沃斯滤波器电路的截止频率为 284 rads / s 或 45.2Hz,最大通带增益为 0.5dB,最小阻带增益为 20dB。
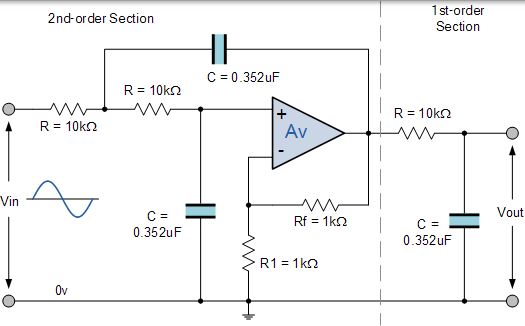
因此对于我们的三阶巴特沃斯低通滤波器,转角频率为 45.2Hz,C = 360nF,R =10kΩ